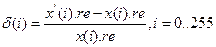Співпроцесора NM6403 при розбитті матриці співпроцесора NM6403 при розбитті матриці

вагових коефіцієнтів - (2х32біти)/(8х8біт) вагових коефіцієнтів - (2х32біти)/(2х32біти)

По приведених двох варіантах розбивки матриці векторного помножувача виробляється повний процес скалярного множення двох комплексних векторів. Перша схема виконує 16 множень з нагромадженням за такт і служить для знаходження сум попарних добутків уявних і дійсних частин, друга виконує 4 множення з нагромадженням за такт, але фактично служить тільки для остаточного додавання отриманих часткових сум. Повна схема множення двох комплексних векторів довжиною 16 елементів відображена на рис.18. Тому що за один раз у матрицю вагових коефіцієнтів можна завантажити тільки 8 елементів вектора [х], завантаження усього вектора [х] відбуваються в два етапи.

Весь процес обчислення скалярного добутку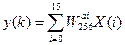складається з трьох етапів:

1. В матрицю вагових коефіцієнтів завантажуються 8 комплексних чисел x(0)..x(7).

На вхід помножувача X по черзі подаються спочатку вектор з 8-ми дійсних частин комплексних

коефіцієнтів W(0)..W(7) (тут 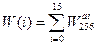), а потім вектор з 8-ми уявних частин. Множення робиться відповідно до схеми на рис.16.

1. Далі з виходу помножувача результат добутку у виді двох 64р. слів безпосередньо надходить на підсумовуючий Y-вхід помножувача . При цьому в матрицю вагових коефіцієнтів завантажуються числа x(8)..x(15), а на вхід X помножувача аналогічно надходять і збільшуються нові коефіцієнти W(8)..W(15).
2. Для одержання остаточного результату -y(k), суми в лівих і правих частинах двох останніх результатів ("3-rd product" і "4-th poduct" ) необхідно перехресно скласти ( з врахуванням знака "-"). Для цього, як показано на рис.6, в матрицю вагових коефіцієнтів завантажуються числа 0,1 і -1, а самі суми подаються на вхід X і Y і далі, працюючи за схемою на рис.5, векторний помножувача видає кінцевий результат для y(k).

Для наочності на рис.18 проілюстрований процес скалярного множення тільки двох векторів. В дійсності завантаження вхідних даних здійснюється пакетами по 32 64-розрядні слова, що дозволяє

максимально ефективно використовувати векторний співпроцесор. В результаті, з врахуванням часу передачі даних кожен крок множення (рис 16, рис 17) практично займає один процесорний такт, це досягається за рахунок одночасного використання двох шин даних - підкачування вхідних даних x(і) по одній шині суміщається з завантаженням коефіцієнтів W(і) чи вивантаженням результатів множення y(і) по іншій. Таким чином, реально вся процедура скалярного множення двох комплексних 16-мірних векторів у середньому по всьому ШПФ-256 складає 7 процесорних тактів.

Рис.18 Послідовність обчислення скалярного добутку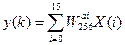

Продуктивність і точність обчислень.

Точність обчислень визначається кількістю біт, що відводяться для представлення коефіцієнтівW. Є два способи представлення значень косинусів і синусів у 8 розрядній сітці:

1. W =round(64.0*cos(x)) - (умовно 6 біт на одиницю)

2. W =round(127.0*cos(x)) - (умовно 7 біт на одиницю)

Перший спосіб має 65 градацій косинуса в діапазоні 0..1, у той час як другий спосіб - 128 і

отже має більш високу точність. Однак, виконуючи в ході обчислень тільки операції цілочисельного множення і додавання, наприкінці необхідно провести нормалізацію результатів, тобто кожен елемент вихідного масиву потрібно поділити на відповідний масштабуючий коефіцієнт. Для першого випадку він дорівнює 642, а для другого - 1272. В обох випадках розподіл доцільний замінити зсувом вправо, але на відміну від першого способу заміна розподілу на 1272 зсувом на 14 біт вправо привносить невелику систематичну похибку. Нормалізацію можна проводити або один раз наприкінці множень, або двічі – після кожного етапу множення (рис.1) (проміжна нормалізація служить для запобігання переповнення в ході обчислень). Кількість необхідних етапів нормалізації визначаться в залежності від діапазону вхідних даних див. табл. 3.

Для оцінки точності довільний сигнал оброблявся прямим і зворотнім перетворенням Фур'є, після

чого вихідний x порівнювався з відновленим сигналом x'. Зокрема , знаходилося математичне сподівання M і середнє квадратичне відхилення s відносних похибок .d.