Основні формули

Теореми, що пояснюють суть перетворення Фур’є (наведені без доведення).

Теорема 1. Якщо комплексне число представлене у вигляді e ^j2πN, де N - ціле, то e ^j2πN = 1.

Теорема 2. Величина періодична по k і по n з періодом N. Тобто, для будь-яких цілих l і m виконується рівність:

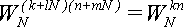(2.4)

Теорема 3.

Для величини справедлива формула:

(2.5)

З наведених теорем визначається основна ідея алгоритму ШПФ:

1. Необхідно розділити суму (1) з N доданків на дві суми по N/2 доданків, і обчислити їх окремо. Для обчислення кожної з підсум, треба їх теж розділити на дві і т.д.

2. Необхідно повторно використовувати вже обчислені доданки.

При обчисленні алгоритму ШПФ застосовують або "проріджування за часом" (в першу суму попадають доданки з парними номерами, а в другу - з непарними), або "проріджування за частотою" (в першу суму попадають перші N/2 доданків, а в другу - інші). Обидва варіанти рівноцінні. В силу специфіки алгоритму доводиться застосовувати тільки N, що є ступенями 2. Розглянемо випадок проріджування за часом.

Теорема 4. Визначимо ще дві послідовності: {x_[even]} і {x_[odd]} через послідовність {x} таким чином:

x_[even]n = x_2n, x_[odd]n = x_2n+1, (2.6)

n = 0, 1,..., N/ 2-1

Нехай до цих послідовностей застосовані ДПФ і отримані результати у вигляді двох нових послідовностей {X_[even]} і {X_[odd]} по N/2 елементів у кожній.

Елементи послідовності {X} можна виразити через елементи послідовностей {X_[even]} і {X_[odd]} за формулою:

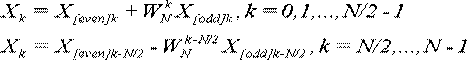(2.7).

Формула (2.7) дозволяє скоротити число множень удвічі (не враховуючи множень при обчисленні X_[even]k і X _[odd]k), якщо обчислювати X_k не послідовно від 0 до N - 1, а попарно: X₀ і X_N/2, X₁ і X_N/2+1,..., X_{N/ 2-1} і X_N. Пари утворяться за принципом: X_k і X_N/2+k.

Теорема 5. ДПФ можна обчислити і за формулою:

(2.8)

З теореми випливає, що можна не зберігати обчислені значення X_[even]k і X_[odd]k після обчислення чергової пари, і одне обчислення можна використовувати для обчислення двох елементів послідовності {X}.

На цьому кроці буде виконане N/2 множень комплексних чисел. Якщо застосувати подібні схеми для обчислення послідовностей {X_[even]} і {X_[odd]}, то кожна з них вимагатиме N/4 множень, разом ще N/2. Продовжуючи аналогічно далі log₂N разів, можна дійти до сум, що містять лише один доданок, так що загальна кількість множень рівна (N/2)log₂N.

Розглянемо ШПФ для різних N. Додамо ще один нижній індекс, який буде вказувати на загальну кількість елементів послідовності, до якої цей елемент належить. Тобто X_{R}k - це k-ий елемент послідовності {X_{R}} з R елементів. X_{R}[even]k - це k-ий елемент послідовності {X_{R}[even]} з R елементів, обчислений по парних елементах послідовності {X_{2R}}. X_{R}[odd]k - це k-ий елемент послідовності {X_{R}[odd]}, обчислений по непарних елементах послідовності {X_{2R}}.

У випадку, коли доданок лише один (N = 1) формула (1) спрощується до:

,

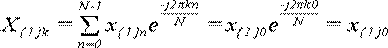Оскільки в цьому випадку k може бути рівне тільки 0, то X_{1}0 = x_{1}0, тобто, ДПФ над одним числом дає це ж саме число.

Для N = 2 за теоремою (2.5) отримаємо:

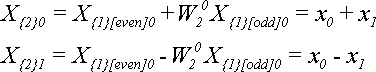
Для N = 4 за теоремою (2.5) отримаємо:

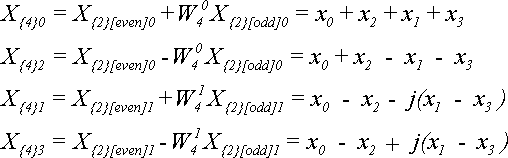
Звідси виходить, що якщо елементи вихідної послідовності були дійсними, то при збільшенні N елементи ДПФ стають комплексними.

Для N = 8 за теоремою (2.5) отримаємо:

Необхідно звернути увагу, що на попередньому кроці використовувалися ступені W₄, а на цьому - ступені W₈. Зайвих обчислень можна уникнути, якщо врахувати, що

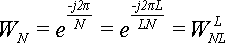
Тоді формули для N=4 будуть використовувати ті ж W-множники, що і формули для N=8:

Висновок:

В основі алгоритму ШПФ лежать такі формули:

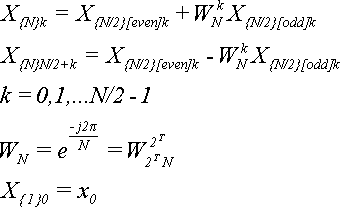(2.9)