Класичні вікна
Всі наведені вікна представляються як парні (щодо початку координат) і містять непарну кількість точок. Для перетворення вікна в ДПФ-парне вікно достатньо відкинути крайню праву точку і зсунути послідовність так, щоб крайня ліва точка співпала з початком координат. Ми будемо використовувати нормовані координати з періодом дискретизації Т=1.0, так що ω0 буде мати період 2π/N і надалі позначатися через θ. Біном ДПФ будемо називати відстань між відліками, кратними 2π/N. Бін має ширину 2π/N.
Прямокутне вікно (вікно Діріхле)
Прямокутне вікно у всьому інтервалі спостереження рівне одиниці. Таке вікно можна розглядати як виділяючу, або стробуючу послідовність, що впливає на вхідну послідовність для виділення з неї кінцевої ділянки. Вікно для кінцевого перетворення Фур'є, що наведено на рис.7.6, визначається як
w(n)=l,0; 
(10.18)
Те ж саме вікно для ДПФ визначається як
w(n)=l,0;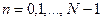 
(10.19)
Спектральне вікно, відповідне прямокутному вікну для ДПФ, дається виразом
(10.20)
Видно, що перетворення цього вікна є ядром Діріхле шириною головного пелюстка ДПФ (між перетинами нуля) 2 біна та рівнем перших бічних пелюстків приблизно на 13 дБ нижче за пік головної пелюстки. Швидкість спаду бічних пелюсток складає 6.0 дБ/октава, що цілком прийнятне для вагової функція з розривами.
Рис 10.7. Прямокутне вікно (а) і логарифм амплітуди його перетворення Фур'є (b).
Тепер, коли дано визначення прямокутного вікна, можна відповісти на поставлене раніше питання: в якому сенсі кінцева сума (10.21) апроксимує нескінченну суму (10.22)
(10.21)
(10.22)
Звідси можна зробити висновок, що кінцева сума – це нескінченна сума, помножена на прямокутну вагову функцію. Нескінченна сума – це розкладання в ряд Фур'є деякої періодичної функції, a f(n) – коефіцієнти цього розкладання. Відзначимо, до речі, і та обставина, що кінцева сума – це просто часткова сума ряду Фур'є.
Трикутне вікно (вікно Фейера і Бартлетта)
Трикутне вікно для кінцевого перетворення Фур'є, що наведене на рис.10.8 визначається виразом
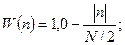
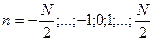(10.23)
Це вікно для ДПФ записується як
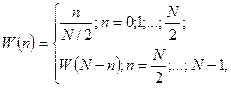(10.24)
Рис. 10.8. Трикутне вікно (а) і логарифм амплітуди його перетворення Фур'є 8(b).
Спектральне вікно, відповідне ДПФ - послідовності, дається формулою
(10.25)
Видно, що перетворення цього вікна є квадратом ядра Діріхле. Ширина його головного пелюстка (між перетинами нуля) удвічі більш ніж в прямокутного вікна, а рівень перших бічних пелюсток рівний приблизно —26 дБ, тобто теж приблизно удвічі нижчий, ніж в прямокутного вікна. Рівень бічних пелюстків спадає із швидкістю 12 дБ/октава, оскільки розривна не сама вагова функція, а тільки її перша похідна. Трикутник – це найпростіше вікно, що має ненегативне перетворення. Такою властивістю володіють всі вікна, отримані шляхом згортки будь-якого вікна (половинної протяжності) з самим собою. Перетворення такого вікна рівно квадрату перетворення початкового вікна.
Вікно, отримане шляхом згортки з початковим вікном, містить приблизно удвічі більше відліків, ніж початкове, і, отже, відповідає тригонометричному поліному (за Z-перетворенням) приблизно удвічі більш високого порядку. (Згортка двох прямокутників по N/2 точок в кожному дасть трикутник з N+1 точок, якщо рахувати нульові точки на кінцях.) Тепер перетворення вікна буде мати удвічі більше нулів, ніж початкове перетворення (це пояснюється збільшенням порядку приєднаного тригонометричного полінома). Перетворення вікна, шляхом згортки з самим собою, просто має кратні нулі в кожній з точок, відповідних нулям початкового перетворення. Завдяки кратності нулів в нуль в цих точках звертається, звичайно, і перша похідна перетворення. Проте, якщо порядок полінома збільшують для зниження рівня бічних пелюсток, подвоєння числа нулів не принесе успіху.
Щоб понизити рівень бічних пелюстків, додаткові нулі слід було б помістити в проміжках між існуючими нулями (поблизу локальних піків бічних пелюсток), а не в тих точках, де перетворення і так рівно нулю.
Вікна виду cosα (X)
Це ціле сімейство вікон, залежних від параметра а, причому а, як правило, ціле число. Привабливість цього сімейства пояснюється легкістю обчислення значень відліків вікна і простотою аналізу властивостей перетворення косинусної функції. Ці якості особливо зручні для ДПФ. Вікно для кінцевого перетворення Фур’є визначається виразом
(10.26)
а для ДПФ – виразом
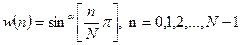(10.27)
В якості α найчастіше вибирають цілі числа від 1 до 4. Найчастіше використовують вікно з α=2 (вікно Хеннінга). Вікна для (α = 1 і 2 даються наступними формулами (для кінцевого перетворення формули з індексом „а", для ДПФ -з індексом "b"):
α =1.0 (косинусоїдальний пелюсток)
(10.28)
α=1.0 (синусоїдальний пелюсток)
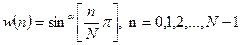(10.29)
α=2.0 (косинус квадрат, підведена косинусоїда, вікно Хеннінга)
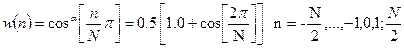(10.30)
α =2.0 (синус квадрат, підведена синусоїда, вікно Хеннінга)
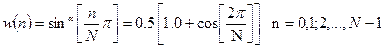(10.31)
Зауважимо, що із зростанням α вікна стають більш гладкими, що відображається і на перетворенні — зменшується рівень бічних пелюстків і швидшає їх спад, зате збільшується ширина головного пелюстка.
Рис. 10.9. Вікно cos4 (пπ/N) (а) і логарифм амплітуди його перетворення Фур’є (b)
Вікна сімейства Гауса (Вейерштрасса) є гладкими функціями, перетворення Фур'є яких має високі вузькі головні пелюстки. Згідно узагальненому принципу невизначеності, не можна одночасно "стиснути" сигнал і його перетворення Фур'є. Якщо мірою стиснення є середньоквадратична часова тривалість Т і середньоквадратична смуга частот W, то, як відомо, для будь-якої функції виконується нерівність
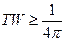(10.33)
Рівність досягається тільки для імпульсу з гаусовою огинаючою. Такий імпульс характеризується мінімальним добутком тривалості на смугу частот і тому досить привабливий для використовування в якості вікна. На жаль, при цьому ми вимушені обрізувати "хвости" гаусовою кривою, тим самим обмежуючи часову тривалість імпульсу. В результаті його спектр розпливається, і добуток тривалості на смугу частот перестає бути мінімальним. Проте, якщо точка усікання лежить за точкою 3σ, помилки усікання малі, і таке вікно є доброю апроксимацією вікна з мінімальним добутком тривалості на смугу частот.
Доцільно знайти такі вікна, які при заданій кінцевій тривалості будуть мати мінімальну ширину смуги. Аналогічна задачу розв’язується при проектуванні антен. Вон полягає у виборі такого розподілу поля в антені кінцевої апертури, які дозволило б якомога більше звузити головну пелюстка діаграми спрямованості, одночасно не допускаючи зростання бічних пелюстків. Рішення, що забезпечує мінімальну ширину головного пелюстка при заданому рівні бічних пелюсток, отримано в замкнутій формі. Воно є вікном (функцію затінення) Дольфа-Чебишева. Безперервне рішення цієї задачі має викиди на межах і тому в безперервних вікнах може бути реалізоване лише приблизно (за допомогою розкладання в ряд Тейлора). Дискретні вікна не мають подібних обмежень, для них можлива точна реалізація рішення.
Співвідношення Tn(X)=cos(θ) задає відображення безлічі поліномів Чебишева n-го алгебраїчного порядку на безліч тригонометричних поліномів того ж порядку. За допомогою цього відображення можна отримати наступний вираз для вікна Дольфа-Чебишева, визначений через значення еквідістантних відліків перетворення Фур'є вікна;
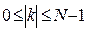(10.34)
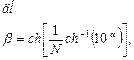
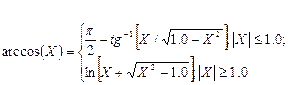
Щоб обчислити відповідні часові відліки вікна ω(n), потрібно просто застосувати до відліків W(k) ДПФ, а потім нормувати їх щодо максимальної амплітуди. Параметр α, характеризує собою логарифм відносини максимуму головної пелюстки до рівня бічних пелюстків. Так α=3.0 відповідає бічним пелюсткам на 3.0 декади (або на 60 дБ) нижчим за головний пелюсток. Множник (-1)x, що змінює знаки послідовних відліків перетворення, введений для обліку зсуву початкової точки в часовій області.