Дискретные сигналы определяются для дискретных значений независимой переменной - времени

 

 

Последовательности и их представления.

 

Дискретные сигналы определяются для дискретных значений независимой переменной - времени.

Время квантуется обычно равномерно:

 

T=nT;

 

Где Т – интервал между отсчетами

Обозначения последовательностей:     1. {h(n)},

Способы получения последовательностей.

1)     Взять набор чисел и расположить их в виде последовательности – 0,1,2,3,…,(N-1) Это образует… 2) Использование рекуррентного соотношения:  

Некоторые важные последовательности.

1)     Цифровой единичный импульс (единичный отсчет)   Его роль такая же, как аналоговый единичный импульс (дельта функция Дирака) в аналоговых системах.

Представление произвольных последовательностей.

 

Рассмотрим последовательность

а(0), а(1), а(2), … , а(n);

 

где а(n) – величина n-го элемента.

 

Такую последовательность можно представить:

Дискретная система.

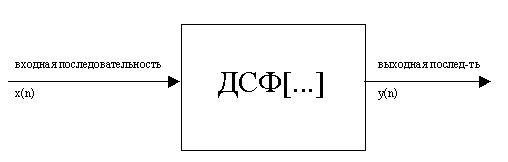
Алгоритм преобразования

 

y(n)=Ф[x(n)]

 

Линейная система.

    x1(n) y1(n)     x2(n) y2(n)  

Система с постоянными параметрами (ЛПП).

    x(n-n0) y(n-n0) – при любых n0   где n0 – величина задержки.

Т.О., чтобы вычислить выходную последовательность системы на заданную входную, необходимо вычислить цифровую свертку входной последовательности и импульсной характеристики системы.

 

Физическая реализуемость.

ЛПП – система физически реализуема, если отклик при n=n0 зависит только от отсчетов входной последовательности с номерами

Это означает, что импульсная характеристика h(n) системы равна нулю, при всех

 

Примеры систем физически нереализуемых.

- Идеальный ФНЧ

- Идеальный дифференциатор.

 

Устойчивость ЛПП.

 

Если при любой ограниченной входной последовательности выходная последовательность так же ограничена.

 

Необходимое и достаточное условие.

Устойчивость системы:     (*)

Т.о. последовательность y (0) не ограничена, так, что неравенство (*) является необходимым условием устойчивости.

Доказательство достаточности.

 

Пусть (*) выполняется. На вход поступает ограниченная последовательность

Тогда:

 

Последовательность y(n) ограничена, поэтому система устойчива, что и требовалось доказать.

 

Примеры импульсных характеристик.

1) Пример устойчивой системы.

2) Пример неустойчивой системы.

Разностные уравнения.

  ,где коэффициенты {ai} и {bi} полностью описывают конкретную систему, как и…  

Частотная характеристика систем первого порядка.

Рассмотрим разностное уравнение: С начальным условием: y(-1)=0  

Частотная характеристика систем второго порядка.

Разностное уравнение:   (для простоты члены при коэффициентах b опущены, т.к. они не влияют на характер изложения).

Единицы измерения частоты

Запись: x(n), y(n), h(n) - опускается период дискретизации Т или – частота… Тогда запись:

Соотношение между непрерывными и дискретными системами.

Спектр: (1) Временная область: (2) Дискретизированный сигнал:

Спектральная функция дискретной последовательности состоит из суммы бесконечного числа спектральных компонент непрерывного колебания.

Если спектр непрерывного колебания ограничен по полосе диапазоном частот , где Т – период дискретизации, т.е. при , то в диапазоне :

С какой частотой дискретизировать непрерывное колебание?

   

При <1 соответствующая система является устойчивой.

 

 

Z-преобразования некоторых последовательностей

Т.к. при всех n, кроме n=0, где x(n)=1, , то: X(z)=1  

Геометрическая интерпретация преобразования Фурье

Преобразование Фурье:

Структурная схема цифровых фильтров.

 

Уравнение цифровой свертки:

Z-преобразование:

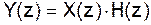
где Y(z) – z-преобразование выходной последовательности,

X(z) - z-преобразование входной последовательности,

H(z) - z-преобразование импульсной характеристики фильтра.

Тогда:

Выразим H(z) в виде дробно-рационального полинома от переменной z^-1, т.е.:

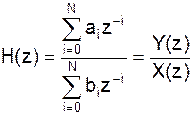
причем b₀ д.б. равно 1.

Приведем к общему знаменателю:

 

Или:

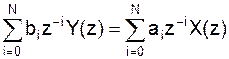
Взяв обратное z-преобразование от левой и правой части (обратное преобразование – не вводилось понятие) можно перейти к последовательностям.

т.к. b₀=1, тогда:

 

- уравнение цифрового фильтра.

Простая форма 1 его реализации:

 

Запишем:

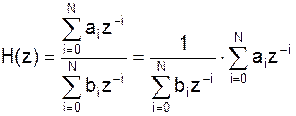
Обозначив первый и второй множители за H1(z) и H2(z) соответственно, можно получить два фильтра:

 

 

*Прямая форма 2 (неканоническая)

 

Очевидно, что можно использовать один набор элементов задержки, т.к. задерживается один и тот же сигнал:

 

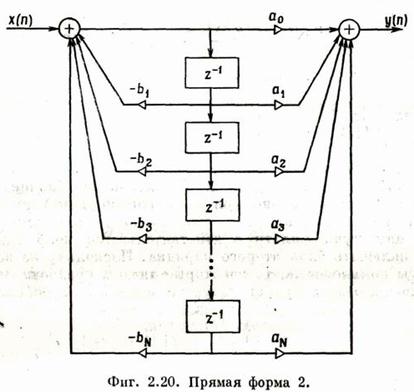
*Прямая форма 2 или каноническая форма

Можно записать:

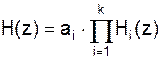
Получим третью структуру построения цифрового фильтра. Множители Hi(z) соответствуют либо блокам второго порядка:

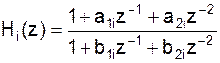
либо блокам первого порядка, т.е.:

 

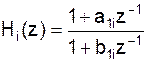
Последовательная (каскадная) форма.

Разложим на простые дроби:

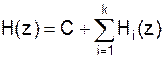
где Hi(z) – соответствуют или блокам второго порядка:

или блокам первого порядка:

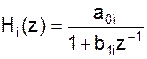
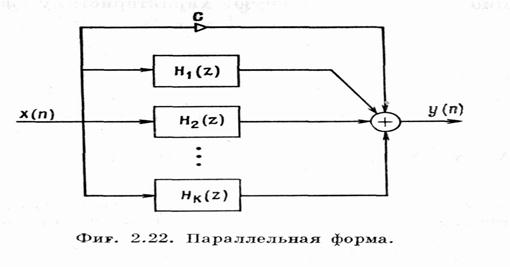
Структурные схемы фильтров без полюсов

В частном случае знаменатель дроби: может быть постоянным. Для простоты приравняем его к единице. При этом разностное уравнение становится нерекурсивным,…

Дискретное преобразование Фурье

- дискретная свертка - преобразование Фурье - z-преобразование.

Свойства ДПФ

xp(n) и yp(n) – периодичные последовательности с периодом N каждая. Xp(к) и Yp(к) – их ДПФ. Тогда для последовательности: xp(n)+yp(n) ДПФ будет равно:

Нерекурсивные цифровые фильтры.

 

 

Порядок расчета фильтров. Свойства КИХ-фильтров. Характеристики КИХ-фильтров с ЛФХ. Частотные характеристики КИХ-фильтров с ЛФХ.

 

Порядок расчета цифрового фильтра

  2. Выбор конкретной схемы построения фильтра и квантование значений его…  

Свойства КИХ-фильтров.

Основные достоинства этих фильтров: 1) Легко создавать КИХ-фильтры со строго линейной фазовой характеристикой.… 2) КИХ-фильтры можно эффективно строить как по рекурсивной, так и по нерекурсивной схемам.

Характеристики КИХ-фильтров с ЛФХ.

Пусть - физически реализуемая последовательность конечной длины, заданная на интервале . Это конечная импульсная характеристика (КИХ). Преобразование Фурье от {h(n)} – частотная характеристика фильтра:

Прямоугольное окно

Весовая функция при при других n.

Метод взве шивания

(*) , где Коэффициенты ряда Фурье, т.е. h(n) – совпадает с коэффициентами импульсной характеристики ЦФ.

Обобщенное окно Хэмминга

при при других n.

Окно Кайзера

Для решения этих задач в непрерывном времени был введен класс так называемых вытянутых сфероидальных волновых функций. Эти функции имеют сложный вид. Кайзер – для их аппроксимации ввел окно, которое называется окном Кайзер:

ФНЧ с различными окнами

Рассмотрим идеальный фильтр нижних частот. Будем использовать 3 окна: - прямоугольное - Хэмминга

Метод частотной выборки

КИХ-фильтр может быть однозначно задан как коэффициентами импульсной характеристики {h(n)}, так и коэффициентами ДПФ от импульсной характеристики… Они связаны соотношениями: (*) - ДПФ

Свойства БИХ-фильтров.

, при Форма записи Z-преобразования импульсной характеристики БИХ-фильтров имеет вид:

Квадрат амплитудной характеристики

При расчете БИХ фильтров с использованием аппроксимации только АЧХ (без учета фазовой характеристики_ удобнее всего оперировать с квадратом амплитудной характеристики:

 

Фазовая характеристика

 

 

Методы расчета коэффициентов БИХ-фильтров

Необходимо решить задачу расчета коэффициентов фильтра ( и ), которые обеспечивали бы аппроксимацию заданных характеристик фильтра таких, как… 1-я группа методов – проектирование соответствующего фильтра непрерывного… 2-я группа методов – прямые методы расчета цифровых БИХ-фильтров. Необходимо найти такое расположение полюсов и нулей…

Расчет БИХ-фильтров по аналоговому прототипу

(*)   причем коэффициенты – известны, S – оператор Лапласа.

Метод инвариантного преобразования импульсной характеристики.

 

Этот метод также называется методом стандартного преобразования.

 

В качестве импульсной характеристики рассчитываемого цифрового фильтра используется дискретизированная импульсная характеристика соответствующего аналогового фильтра.

 

Передаточная характеристика аналогового фильтра:

 

(*) Разложим на простые дроби,

где

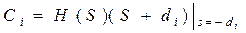
Предположение, что M<N (* - разложение на простые дроби) – является в данном случае обязательным, в противном случае наложения в частотной области станут недопустимыми.

 

Импульсная характеристика h(t) аналогового фильтра:

 

Дискретизируя ее получим.

 

,

где Т – период дискритизации.

 

Найдем Z – преобразование.

 

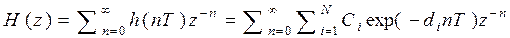
Изменим порядок суммирования.

 

 

(**)

 

 

Сравним (*) (**), переход от H(s) к H(z) осуществляется с помощью отображения, при котором используется замена:

 

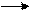Частотная характеристика цифрового фильтра, рассчитанная методом инвариантного преобразования импульсной характеристики, образуется путем положения частотной характеристики дискретизуемого аналогового фильтра.

Т.о.

,

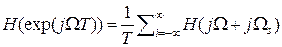где

- угловая частота дискретизации цифрового фильтра

 

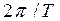Каждая горизонтальная полоса, шириной из S – плоскости отображается на Z – плоскость.

 

Все смежные полосы из S – плоскости будут при отображении накладываться друг на друга в Z – плоскости.

 

Отсюда следует, что для того что бы частотные характеристики исходного аналогового фильтра и рассчитываемого методом инвариантного преобразования импульсной характеристики цифрового фильтра соответствовали друг другу, необходимо что бы полоса пропускания аналогового фильтра находилась в пределах диапазона.

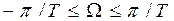
Для выполнения этого условия необходимо до начала преобразования (т.е. до АЦП) вводить дополнительный фильтр нижних частот, гарантирующий соответствующее ограничение полосы пропускания аналогового фильтра.

 

Билинейное Z – преобразование.

  Вся ось jw перейдет в единичную окружность, левая полуплоскость окажется… Учитывая, что:

Согласованное Z – преобразование.

Непосредственное отображение полюсов и нулей из S – плоскости в полюсы и нули на Z – плоскости. Полюс (или нуль) в точке s = - a плоскости s отображается в полюс (или нуль) в… Т.о. имеет место замена:

Обзор методов расчета аналоговых фильтров нижних частот.

Стандартные типы аналоговых фильтров: - Баттерворта - Чебышева 1 типа

Фильтры Баттерворта.

Апроксимация по Баттерворту – фильтры НЧ имеют максимально гладкую амплитудную характеристику в начале координат в S – плоскости. Для частоты среза:  

Фильтры второго типа.

    где Ωr - наименьшая частота, на которой достигается заданный уровень ослабления.

Эллиптические фильтры.

Характеризуются тем, что их амплитудная характеристика имеет равновеликие пульсации в полосе пропускания и в полосе не пропускания. Можно показать, что с точки зрения минимальной ширины переходной полосы…

Частотные преобразования.

Рассмотрим методы расчета ФНЧ непрерывных во времени, а так же методы их дискретизации. При расчете цифровых фильтров ВЧ, ПФ и режекторных,…   1.

Преобразование полосы частот аналоговых фильтров.

    ФНЧ ФНЧ      

Преобразование полосы для ЦФ.

ФНЧ с частотой среза в другой ФН с частотой среза а так же В ФВЧ, ППФ и ПЗФ  

Прямые методы рассчета цифровых фильтров.

 

Существуют так же прямые методы расчета цифровых фильтров в частотной или временной областях, без аналоговых прототипов.

 

Расчет ЦФ по квадрату амплитудной характеристики.

Квадрат амплитудной характеристики: (*)

Расчет БИХ фильтров во временной области.

Это расчет по заданной импульсной характеристике Z – преобразование импульсной характеристики h(k) равно. Требуется, что бы импульсная характеристика h(k) аппроксимировала заданную последовательность g(k) в диапазоне

Алгоритм БПФ с основанием 2.

  W – является периодической последовательностью с периодом N.

Алгоритм БПФ с прореживанием по частоте.

Другая распространенная форма алгоритма БПФ при условии, что N – равно степени 2 – алгоритм БПФ с прореживанием по частоте.   Разобьем входную последовательность x(n) на две равные последовательности.

Вычисление обратного ДПФ с помощью алгоритма БПФ.

Обратное ДПФ N – точечной последовательности {X(k)}; k=0, 1, … , N-1