Дискретное преобразование Фурье

Методы описания последовательностей или дискретных систем:

- дискретная свертка

- преобразование Фурье

- z-преобразование.

 

Когда последовательность периодична или конечна, то ее можно представить рядом Фурье:

Рассмотрим последовательность x(n) – периодическую с периодом N отсчетов.

Тогда можно представить:

(*)

причем частоты спектральных составляющих могут принимать значение только:

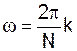, где

т.к. периоды других частот не кратны N.

В уравнении (*) коэффициенты Xp(k) – амплитуды синусоид с частотами ω_р

Учитывая избытычность записи (*), т.е.:

, где 0<n<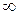

можно записать:

,

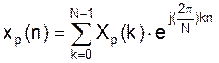т.е. наличие всего N (k=0…n-1) – комплексных синусоид с периодом N-отсчетов.

Для удобства можно записать:

(**)

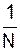- операция нормировки не изменяет способа представления.

 

Соотношение (**) – носит название обратного дискретного преобразования Фурье (ОДПФ).

Можно показать, что коэффициенты 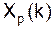определяются:

(***)

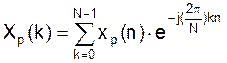
Это соотношение (***) называется дискретным преобразованием Фурье (ДПФ).

Из (**) и (***) видно, что обе последовательност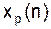и и 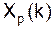периодичны с периодом N-отсчетов.

Ясно также, что X_p(k) полностью определяется одним периодом x_p(n).

Рассмотрим последовательность конечной длины:

при

при других n.

Z-преобразование:

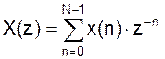
Вычисляя эту сумму при , т.е. в точках на единичной окружности с полярным углом 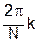, получим:

,

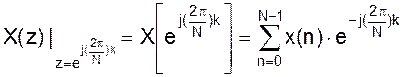т.е. учитывая, что x_p(n)=x(n) на интервале 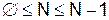, получим:

 

Вывод 1:

Коэффициенты ДПФ последовательности конечной длины равны значениям z-преобразования этой же последовательности в N-точках, равномерно распределенных по единичной окружности.

Вывод 2:

Коэффициенты ДПФ последовательности конечной длины однозначно представляют саму последовательность, т.к. по ним можно точно восстановить саму последовательность, используя обратное ДПФ.

Вывод 3:

Хотя ДПФ и ОДПФ вводятся для периодических последовательностей, важно, что через них можно представлять последовательности конечной длины.