Алгоритм БПФ с основанием 2.

ДПФ конечной последовательности {x(n)} определено ранее:

 

W – является периодической последовательностью с периодом N.

 

Иногда записывают вместо

Подчеркивая периодичность с периодом N.

 

Если x(n) – комплексная последовательность, то из (*) при вычислении N-точечного ДПФ нужно вычислить

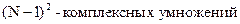
N(N-1) – комплексных сложений.

 

Идея БПФ: разбить исходную последовательность из N – отсчетов на две более короткие т.о. что бы ДПФ всей последовательности было вычислено исходя из этих двух.

 

Рассмотрим N-точечную последовательность {x(n)}, считая, что N=степень 2, т.е.

N=2, 4, 8, 16, 32, 64, 128, 256, …

Возьмем две последовательности

{x1(n)} и {x2(n)} из четных и нечетных отсчетов последовательности {x(n)}

 

x1(n)=x(2n) n=0, 1, … , (N/2) – 1

x2(n)=x(2n+1) n=0, 1, … , (N/2) – 1

 

N – точечные ДПФ последовательности x(n)

 

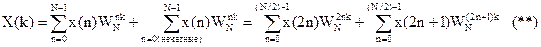
Учитывая, что

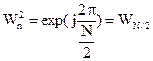
Перепишем (**)

 

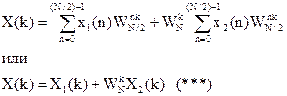
,где X1(k) и X2(k) равны соответственно (Т/2) – точечным ДПФ последовательностей x1(n) и x2(n). Из (***) следует, что N – точечное ДПФ может быть разложено на два (N/2) – точечных ДПФ.

 

Т.к. X(k) определено при

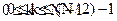
А X1(k) и X2(k) определено при

То необходимо доопределить формулу (***)

x1(0)=x(0) X1(0) X(0)

x1(1)=x(1) X1(1) X(1)

x1(2)=x(2) X1(2) X(2)

x1(3)=x(3) X1(3) X(3)

 

x2(0)=x(0) X2(0) X(0)

x2(1)=x(1) X2(1) X(1)

x2(2)=x(2) X2(2) X(2)

x2(3)=x(3) X2(3) X(3)

 

Квадраты – четырехточечные ДПФ.

 

Первый столбец – разбивка на x(n) последовательностей x1(четн) x2(нечетн)

 

Аналогично N/2 – точечные ДПФ могут быть записаны как комбинация двух N/4 – точечных ДПФ и т.д.

 

Процесс уменьшения размера ДПФ может быть продолжен до тех пор, пока не останутся только двухточечные ДПФ.

Двухточечное ДПФ может быть вычислено по формуле:

 

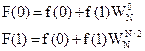
Т.о. вычисляется восьми точечная ДПФ.

 

Восьми точечное ДПФ, полученное последовательным прореживанием в 2 раза – БПФ.

 

О – операция +и

- - операция умножения.

 

a a+b

 

O

b a-b

 

 

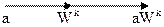
Этот алгоритм БПФ называется алгоритмом БПФ с основанием два с прореживанием по времени.

 

Свойства алгоритма БПФ с основанием 2 и прореживанием по времени.

 

1. На каждом этапе БПФ (т.е. при каждом сокращении размеров БПФ) необходимо выполнить N/2 - комплексных умножений.

2. Общее количество этапов сокращения равно.

3.
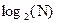
Общее число комплексных умножений равно

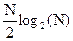Базовая операция алгоритма с прореживанием по времени (так называемая «бабочка» или «батерфляй») состоит в следующем:

4.
Для выполнения БПФ N – точечной последовательности, размещенной в памяти, достаточно иметь лишь одну дополнительную ячейку памяти.

5. Результаты всех промежуточных этапов БПФ можно размещать в те же ячейки памяти, где находились исходные ячейки памяти.

 

6. Перестановка данных и двоичная инверсия.

 

 

Для 8-ми точечного БПФ необходим такой порядок следования отсчетов.

 

x(0), x(4), x(2), x(6), x(1), x(5), x(3), x(7);

 

В случае, когда N – равно степени 2, входная последовательность должна быть разложена в двоично-инверсном порядке для того, что бы выходная последовательность получалась в прямом.

 

Номер	Двоичное представление	Двоичная инверсия	Двоичный инв. номер.

 

7. На всех этапах БПФ используются коэффициенты

 

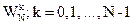
Алгоритм БПФ с прореживанием по частоте. Обратное ДПФ с помощью алгоритма обратного ДПФ. Алгоритмы БПФ с основанием 2.