Разностные уравнения.

В общем виде линейное разностное уравнение М-го порядка с постоянными коэффициентами имеет вид:

 

,где коэффициенты {ai} и {bi} полностью описывают конкретную систему, как и импульсная характеристика. При любом входном сигнале можно определить выходной.

 

Разностные уравнения – это алгоритм функционирования системы.

Зная входную последовательность x(m) и начальные условия:

x(n-1), x(n-2), … , y(n-1), y(n-2), …

Всегда можно определить соответствующую ей выходную последовательность y(n).

 

Рассмотрим разностное уравнение первого порядка.

 

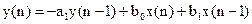
Этому уравнению соответствует система, схема реализации которой имеет вид:

Элемент задержки осуществляет задержку последовательности на один отсчет.

 

Разностное уравнение второго порядка:

Схема имеет вид:

Частотная характеристика.

 

При подаче на вход последовательностей вида:

 

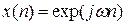
На выходе ЛПП - систем последовательность y(n) будет совпадать с входной, умноженной на некоторый комплексный коэффициент, зависящий только от частоты гармонического сигнала.

 

Выходная последовательность:

 

 

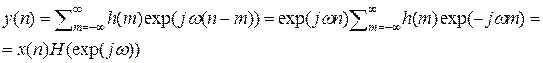
Множитель называется частотной характеристикой ЛПП – систем, т.к. он представляет коэффициент передачи ЛПП – систем для каждого значения частоты.

 

Пример:

 

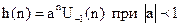
Пусть

Частотная характеристика:

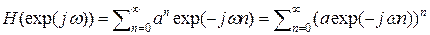
Т.к., то сумма геометрической прогрессии будет равна:

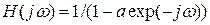
Свойства частотной характеристики:

1. Частотная характеристика является периодической функцией.

2. 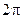Ее период равен

3. 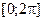Достаточно ее знать на интервале

4. Для действительных h(n) (что часто бывает на практике) модуль

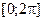
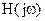
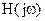- симметричен, а фаза антиметрична на интервале

5. Поэтому часто частотную характеристику задают на интервале