Частотная характеристика систем второго порядка.

Разностное уравнение:

(для простоты члены при коэффициентах b опущены, т.к. они не влияют на характер изложения).

Введем начальные условия: y(-1)=y(-2)=0

Структурная схема системы:

Члены b1 x(n-1) и b2 x(n-2) – опущены для простоты изложения.

Можно показать, что импульсная характеристика может принять одну из двух форм:

(*)

где р1 и р2 – действительные числа.

Либо:

(**)

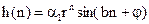Импульсная характеристика (*) – описывает две системы первого порядка и убывает, как:

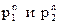
Выражение (**) описывает систему второго порядка, импульсная характеристика – затухающая синусоида.

Условие для импульсной характеристики вида (**)

(***)

отсюда a2<0

Это условие (***) выполняется тогда, когда:

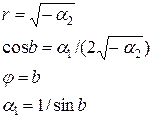
Частотная характеристика:

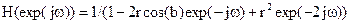
Дискретный ряд Фурье

Рассмотрим частотную характеристику системы с импульсной характеристикой h(n):

(*) ; - периодическая функция частоты

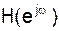- можно рассматривать как разложение в ряд Фурье, причем коэффициенты разложения являются одновременно отсчетами импульсной характеристики системы. Согласно теории рядов Фурье, коэффициенты h(n) можно выразить:

(**)

Т.о. эти два равенства (*) и (**) представляют собой пару преобразований Фурье.

h(n) – суперпозиция синусоид с амплитудами .

Для произвольной входной последовательности x(n):

И

Можно показать, что:

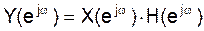
Ранее получали:

Т.о. отклик системы во временной области y(n) есть цифровая свертка импульсной характеристики h(m) и входной последовательности x(n) или

В частотной области: преобразование Фурье от выходной последовательности есть умножение преобразования Фурье от входной последовательности и частотной характеристики системы 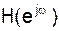.