Построение компьютерной модели трубчатого реактора в нестационарном режиме.

 

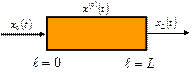
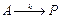
2.1. Основные допущения:

 

· изотермический режим;

· однопараметрическая диффузионная модель.

 

2.2. Уравнение математического описания:

 

 

 

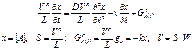
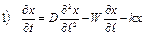
Уравнение 1) является дифференциальным уравнением в частных производных второго порядка параболического типа с двумя независимыми переменными t и 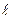и описывает нестационарный режим трубчатого реактора, в котором протекает единственная простейшая реакция, если принята однопараметрическая диффузионная модель для потока.

 

Необходимо найти:

 

 

 

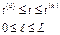
Начальное условие:

 

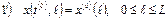
Граничные условия:

 

 

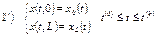
Для решения системы дифференциальных уравнений в частных производных (СДУЧП) может быть использован метод дискретизации, в соответствии с которым производные представляются в конечно-разностной форме в определённом интервале 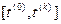и/или [0, L] в результате чего уравнение 1) с начальным 1’) и граничными 1’’) условиями превращаются в систему обыкновенных дифференциальных уравнений (СОДУ) и/или в систему конечных уравнений (СКУ).

 

Для этого уравнения можно использовать три варианта дискретизации:

1) По независимой переменной :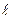

 

В результате получается система обыкновенных дифференциальных уравнений 1-го порядка с независимой переменной t .

 

2) По независимой переменной t :

 

 

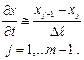
В результате получается система обыкновенных дифференциальных уравнений 2-го порядка с независимой переменной .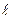

 

3) По независимым переменным 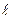и t :

 

 

 

 

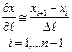
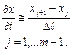
В результате получается система конечных уравнений.

Детально рассмотрим 1-й вариант дискретизации по независимой переменной :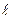

 

 

 

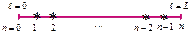
При 0 < 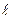< L конечно-разностное представление производных имеет вид:

- Производная «по недостатку»:

 

 

- Производная «по избытку»:

 

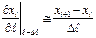
- Вторая производная:

 

 

 

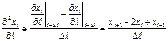
В этом случае граничные условия 1’’) равны:

 

 

 

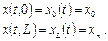
В результате из одного уравнения в частных производных вследствие дискретизации получается система (n-1) обыкновенных дифференциальных уравнений с независимой переменной t и начальным условием 1’), представленным в дискретном виде:

 

 

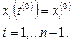
Если для конечно-разностного представления производной использовать «производную по избытку», то система обыкновенных дифференциальных уравнений с начальными условиями имеет вид:

Преобразуя уравнение 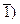и

 

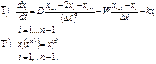предполагая, что его параметры являются константами (D, W и k), можно получить следующую систему обыкновенных дифференциальных уравнений:

 

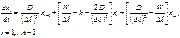
или

 

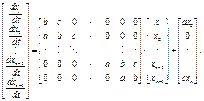
где

 

 

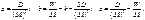
Из изложенного следует, что система уравнений 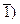включает граничные условия и в матричном виде может быть представлена:

 

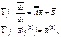
где - вектор с граничными условиями, а начальные условия являются дискретным представлением начального условия

 

Полученная система неоднородных обыкновенных дифференциальных уравнений может быть легко решена любым из известных методов (например, методом Эйлера или Рунге-Кутта), тем более потому, что матрица её коэффициентов 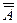является трёхдиагональной.