Булева алгебра

Чтобы описать схемы, получаемые сочетанием различных вентилей, нужен особый тип алгебры, в которой все переменные и функции могут принимать только два значения: 0 и 1. Такая алгебра называется булевой. Она названа в честь английского математика Джорджа Буля (1815-1864). На самом деле в данном случае мы говорим об особом типе булевой алгебры, а именно — об алгебре релейных схем, но термин «булева алгебра» очень часто используется в значении «алгебра релейных схем», поэтому мы не будем их различать.

Как и в обычной алгебре (то есть в той, которую изучают в школе), в булевой алгебре есть свои функции. Булева функция на входе получает одну или несколько переменных и выдает результат, который зависит только от значений этих переменных. Можно определить простую функцию F, сказав, что F(A) = 1, если А = 0, и F(А) = 0, если А = 1. Такая функция будет функцией НЕ (см. рис. 3.2, а).

Так как булева функция от n переменных имеет только 2n возможных комбинаций значений переменных, то такую функцию можно полностью описать в таблице с 2n строками. В каждой строке будет даваться значение функции для разных комбинаций значений переменных. Такая таблица называется таблицей истинности. Все таблицы на рис. 3.2 представляют собой таблицы истинности.

Если мы договоримся всегда располагать строки таблицы истинности по порядку номеров, то есть для двух переменных в порядке 00, 01, 10, 11, то функцию можно полностью описать 2n-разрядным двоичным числом, которое получается, если считывать по вертикали колонку результатов в таблице истинности. Таким образом, НЕ-И - это 1110, НЕ-ИЛИ - 1000, И - 0001 и ИЛИ - 0111. Очевидно, что существуют только 16 булевых функций от двух переменных, которым соответствуют 16 возможных 4-разрядных цепочек. В обычной алгебре, напротив, есть бесконечное число функций от двух переменных, и ни одну из них нельзя описать, дав таблицу значений этой функции для всех возможных значений входных переменных, поскольку каждая переменная может принимать бесконечное число значений.

На рис. 3.3, а показана таблица истинности для булевой функции от трех переменных: М = F(A, B, С). Это функция большинства, которая принимает значение 0, если большинство переменных равны 0, или 1, если большинство переменных равны 1. Хотя любая булева функция может быть определена с помощью таблицы истинности, с возрастанием количества переменных такой тип записи становится громоздким. Поэтому вместо таблиц истинности часто используется другой вариант записи.

Чтобы увидеть этот другой тип записи, отметим, что любую булеву функцию можно определить, указав, какие комбинации значений входных переменных приводят к единичному значению функции. Для функции, приведенной на рис. 3.3, а, существует 4 комбинации переменных, которые дают единичное значение функции. Мы будем рисовать черту над переменной, показывая, что ее значение инвертируется. Отсутствие черты означает, что значение переменной не инвертируется.

Кроме того, мы будем использовать знак умножения (точку) для обозначения булевой функции И (этот знак может опускаться) и знак сложения (+) для обозначения булевой функции ИЛИ. Например, AВС принимает значение 1, только если A = 1,B = 0 и С=1. Кроме того, АВ + ВС принимает значение 1, только если (А = 1 и В = 0) или (В = 1 и С = 0). В таблице на рис. 3.3, а функция принимает значение 1 в четырех строках: 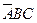, , и ABC, Функция М принимает значение истины (то есть 1), если одно из этих четырех условий истинно. Следовательно, мы можем написать

М = 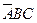+++ ABC.

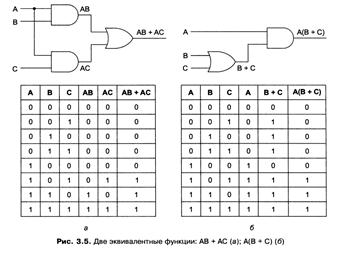
Разработчики схем часто стараются сократить число вентилей, чтобы снизить цену, уменьшить занимаемое схемой место, сократить потребление энергии и т. д. Чтобы упростить схему, разработчик должен найти другую схему, которая может вычислять ту же функцию, но при этом требует меньшего количества вентилей (или может работать с более простыми вентилями, например, двухвходовыми вместо четырехвходовых). Булева алгебра является ценным инструментом в поиске эквивалентных схем.