рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Ядерная техника
- /
- КВАНТОВАЯ МЕХАНИКА АТОМНАЯ ФИЗИКА И СПЕКТРОСКОПИЯ ЭЛЕМЕНТЫ ЯДЕРНОЙ ФИЗИКИ
Реферат Курсовая Конспект
КВАНТОВАЯ МЕХАНИКА АТОМНАЯ ФИЗИКА И СПЕКТРОСКОПИЯ ЭЛЕМЕНТЫ ЯДЕРНОЙ ФИЗИКИ
КВАНТОВАЯ МЕХАНИКА АТОМНАЯ ФИЗИКА И СПЕКТРОСКОПИЯ ЭЛЕМЕНТЫ ЯДЕРНОЙ ФИЗИКИ - раздел Ядерная техника, Министерство Образования И Науки ...
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Quot;САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА
(национальный исследовательский университет)"
КВАНТОВАЯ МЕХАНИКА
АТОМНАЯ ФИЗИКА И СПЕКТРОСКОПИЯ
ЭЛЕМЕНТЫ ЯДЕРНОЙ ФИЗИКИ
Задачи для аудиторной и самостоятельной работы
Самара 2012
Составители: Е.А.Китаева, В.Г. Макарян, И.Л. СтукалинаЗадачи
1Температура абсолютно черного тела изменилась при нагревании от 1000 К до 3000 К. Во сколько раз увеличилась при этом его энергетическая светимость? На сколько изменилась длина волны, на которую приходится максимум спектральной плотности энергетической светимости? Во сколько раз увеличилась его максимальная спектральная плотность энергетической светимости?
2Абсолютно черное тело имеет температуру 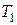 =2900 К. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на 9 мкм. До какой температуры
=2900 К. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на 9 мкм. До какой температуры 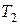 охладилось тело?
охладилось тело?
3Радиус вольфрамовой нити в электрической лампочке равен 0,2 мм, длина равна 5 см. При включении лампочки в цепь с напряжением 220 В через лампочку течет ток силой 0,27 А. Найти температуру нити лампочки. Считать, что в состоянии равновесия все выделяющееся в нити тепло теряется в результате лучеиспускания. Коэффициент черноты для вольфрама при этой температуре равен 0,31.
4Энергетическая светимость абсолютно черного тела равна 3 Вт/см2. Определить длину волны, отвечающую максимуму испускательной способности этого тела.
5Излучение солнца по спектральному составу близко к излучению абсолютно черного тела, для которого длина волны, соответствующая максимуму спектральной плотности энергетической светимости равна 0,48 мкм. Найти массу, теряемую солнцем ежесекундно за счет излучения. Оценить время, за которое масса солнца уменьшится на 1%.
6Два абсолютно черных тела имеют одинаковую температуру 1000 К. Площадь поверхности одного тела в два раза меньше площади поверхности второго тела. Первое тело охлаждают на 500 К. На сколько нужно нагреть второе тело, чтобы общая энергетическая светимость тел не изменилась?
7Медный шарик радиусом 0,6 см поместили в откачанный сосуд, температура стенок которого поддерживается близкой к абсолютному нулю. Начальная температура шарика 300 К. Считая поверхность шарика абсолютно черной, найти, через сколько времени его температура уменьшится в 2 раза.
8Поверхность тела нагрета до температуры 1000 К. Затем одна половина этой поверхности нагревается на 100 К, а другая охлаждается на 100 К. Во сколько раз изменится энергетическая светимость поверхности этого тела?
9Какую мощность надо подводить к зачерненному металлическому шарику радиусом 2 см, чтобы поддерживать его температуру на 27 К выше температуры окружающей среды? Температура окружающей среды равна 293 К. Считать, что тепло теряется только вследствие излучения.
10Температура абсолютно черного тела равна 2 кК. Определить: а) спектральную плотность энергии для длины волны λ=600 нм; б) объемную плотность энергии в интервале длин волн от λ1=590 нм до λ1=610 нм. Принять, что средняя спектральная плотность энергии тела в этом интервале равна значению, найденному для длины волны λ=600 нм.
11Исследование спектра излучения солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ=500 нм. Принимая солнце за абсолютно черное тело, определить: а) энергетическую светимость солнца; б) поток энергии, излучаемый солнцем; в) массу электромагнитных волн (всех длин), излучаемых солнцем за 1 с.
12Муфельная печь потребляет мощность Р = 1 кВт. Температура ее внутренней поверхности при открытом отверстии площадью S = 25 см2 равна 1,2 кК. Считая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками.
Ответы
1. 81; 1,93 мкм; в 243 раза. 2. 290 К. 3. 2700 К. 4. 3,4 мкм. 5.  ;
; 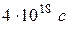 . 6. 100 К. 7. 3 часа. 8. 1,06. 9. 3 Вт. 10. 30 109 Вт/м3. 11. 64 МВт/м2; 3,9 1026 Вт; 4,3 109 кг. 12. 0,71.
. 6. 100 К. 7. 3 часа. 8. 1,06. 9. 3 Вт. 10. 30 109 Вт/м3. 11. 64 МВт/м2; 3,9 1026 Вт; 4,3 109 кг. 12. 0,71.
Квантовые свойства света. Фотоэффект
Вопросы:
1 Фотоны и их характеристики: энергия, масса и импульс.
2 Фотоэффект.
3 Законы фотоэффекта.
Принятые обозначения:
·  – релятивистская масса фотона.
– релятивистская масса фотона.
·  – энергия фотона.
– энергия фотона.
· W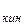 – кинетическая энергия.
– кинетическая энергия.
· e – заряд электрона.
· ω – циклическая частота световой волны.
· ν – частота световой волны.
· 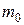 – масса покоя
– масса покоя
· 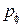 – импульс фотона
– импульс фотона
· λ – длина световой волны
· U – задерживающее напряжение
– задерживающее напряжение
·  − ток насыщения
− ток насыщения
· 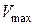 − максимальная скорость фотона
− максимальная скорость фотона
· 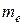 - масса электрона
- масса электрона
· 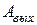 - работа выхода электрона из металла.
- работа выхода электрона из металла.
· 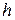 − постоянная Планка.
− постоянная Планка.
· w0, n0 – минимальные частоты.
· l0 – максимальная длина волны.
Основные формулы:
· Энергия фотона:
 .
.
· Масса фотона:
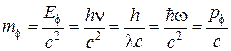 .
.
· Импульс фотона:
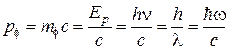 .
.
· Формула Эйнштейна для фотоэффекта:
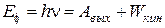 ,
,
где: а) 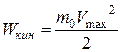 , если
, если 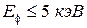 ;
;
б) 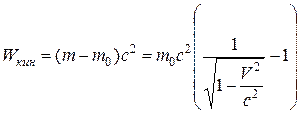 , если
, если  .
.
· Красная граница фотоэффекта:

 ,
,  ,
, 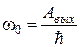 .
.
· Задерживающий потенциал:
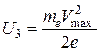 .
.
Задачи
1При поочередном освещении поверхности некоторого металла светом с длиной волны 0,35 мкм и 0,54 мкм обнаружили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в два раза. Найти работу выхода с поверхности этого металла.
2Определить максимальную скорость фотоэлектронов, вырываемых с поверхности серебра: а) ультрафиолетовым излучением с длиной волны  мкм; б)
мкм; б) 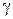 -излучением с длиной волны
-излучением с длиной волны 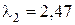 пм, если работа выхода электронов из серебра равна 4,7 эВ.
пм, если работа выхода электронов из серебра равна 4,7 эВ.
3Определить красную границу λο фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны λ=400 нм максимальная скорость фотоэлектронов равна 0,65 Мм/с.
4Для прекращения фотоэффекта, вызванного облучением ультрафиолетовым светом платиновой пластинки, нужно приложить задерживающую разность потенциалов  =3,7 В. Если платиновую пластинку с работой выхода
=3,7 В. Если платиновую пластинку с работой выхода 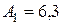 эВ заменить другой пластинкой, то задерживающую разность потенциалов придется увеличить до 6 В. Определить работу выхода
эВ заменить другой пластинкой, то задерживающую разность потенциалов придется увеличить до 6 В. Определить работу выхода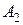 электронов с поверхности этой пластинки.
электронов с поверхности этой пластинки.
5Определить максимальную скорость фотоэлектронов, вылетающих из металла при облучении 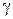 -фотонами с энергией 1,53 МэВ.
-фотонами с энергией 1,53 МэВ.
6Максимальная длина волны света, вызывающего фотоэффект с поверхности пластины равна 0,5 мкм. Если на эту пластину подать задерживающий потенциал, равный 2 В, то при какой минимальной частоте начнётся фотоэффект?
7Лазер мощностью 1 мВт генерирует монохроматическое излучение с длиной волны равной 0,6 мкм. За какое время лазер испускает фотоны, суммарная масса которых равна массе покоя протона ( )?
)?
8Сетчатка глаза начинает реагировать на жёлтый свет с длиной волны 600 нм при мощности падающего на него излучения 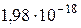 Вт. Сколько фотонов при этом падает на сетчатку каждую секунду?
Вт. Сколько фотонов при этом падает на сетчатку каждую секунду?
9Найти массу фотона, импульс которого равен импульсу молекулы водорода при температуре t = 20 °С. Скорость молекулы считать равной средней квадратичной скорости.
10Найти частоту ν света, вырывающего из металла электроны, которые полностью задерживаются разностью потенциалов 3 В. Фотоэффект прекращается при частоте света 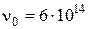 Гц. Найти работу выхода электрона из металла.
Гц. Найти работу выхода электрона из металла.
11Фотон с λ=0,170 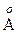 вырывает из покоившегося атома электрон, энергия связи которого Е = 69,3 кэВ. Найти импульс, переданный атому в результате этого процесса, если электрон вылетел под прямым углом к направлению падающего фотона.
вырывает из покоившегося атома электрон, энергия связи которого Е = 69,3 кэВ. Найти импульс, переданный атому в результате этого процесса, если электрон вылетел под прямым углом к направлению падающего фотона.
12При некотором максимальном значении задерживающей разности потенциалов фототок с поверхности лития (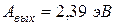 ), освещаемого светом с длиной волны λo, прекращается. Изменив длину волны света в n=1,5 раза, установили, что для прекращения тока необходимо увеличить задерживающую разность потенциалов в
), освещаемого светом с длиной волны λo, прекращается. Изменив длину волны света в n=1,5 раза, установили, что для прекращения тока необходимо увеличить задерживающую разность потенциалов в 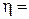 2,0 раза. Вычислить λο.
2,0 раза. Вычислить λο.
Ответы
1. 1,9 эВ. 2.  м/с;
м/с; 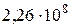 м/с. 3. 651 нм. 4. 4 эВ. 5.
м/с. 3. 651 нм. 4. 4 эВ. 5. 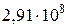 м/с. 6.
м/с. 6.  Гц. 7.
Гц. 7. 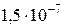 с. 8.
с. 8.  . 9.
. 9. 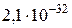 кг. 10.
кг. 10.  Гц. 11.
Гц. 11. 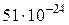 кг м/с. 12.
кг м/с. 12.  м.
м.
Давление света. Эффект Комптона
Вопросы:
1 Давление света.
2 Эффект Комптона.
Принятые обозначения:
· p – давление.
· 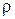 - коэффициент отражения.
- коэффициент отражения.
· Ee – облучённость поверхности.
· w – объёмная плотность энергии излучения.
· 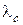 – комптоновская длина волны.
– комптоновская длина волны.
Основные формулы:
· Давление света при нормальном падении:
 или
или 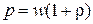
· Изменение длины волны Dl фотона при рассеянии его на электроне на угол q: 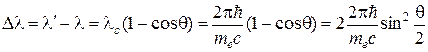
· Комптоновская длина волны:
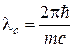 (при рассеивании на электроне
(при рассеивании на электроне 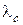 = 2.436 пм).
= 2.436 пм).
Задачи
1Стенка колбы у электролампы накаливания представляет собой посеребренную сферу радиусом 4 см. Лампа потребляет мощность 50 Вт, 90% которых затрачивается на излучение. Во сколько раз давление газа в колбе, равное 1,5 мкПа, меньше светового давления?
2Небольшое идеально отражающее зеркальце массы 10 мг подвешено на невесомой нити длины 10 см. Найти угол, на который отклонится нить, если по нормали к зеркальцу в горизонтальном направлении произвести выстрел коротким импульсом лазерного излучения с энергией 13 Дж?
3Пучок монохроматического света с длиной волны 663 нм падает нормально на зеркальную плоскую поверхность. Поток энергии имеет мощность 0,6 Вт. Определить силу давления, испытываемую этой поверхностью, а также число фотонов, падающих на нее за время 5 с.
4Параллельный пучок света длиной волны λ=500 нм падает нормально на зачерненную поверхность, производя давление p = 10 мкПа. Определить: а) концентрацию фотонов в пучке; б) число фотонов, падающих на поверхность площадью 1 м2 за время 1 с.
5Русский астроном Ф.А. Бредихин объяснил форму кометных хвостов световым давлением солнечных лучей. Найти световое давление солнечных лучей на абсолютно черное тело, помещенное на таком же расстоянии от Солнца, как и Земля. Какую массу должна иметь частица в кометном хвосте, помещенная на этом расстоянии, чтобы сила светового давления на нее уравновешивалась силой притяжения частицы Солнцем? Площадь частицы, отражающую все падающие на нее лучи, считать равной S =0,5·10-12 м2. Солнечная постоянная K = 1,37 кВт/м2.
6Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. При этом длина волны излучения, рассеянного под углами 60 и 120 градусов отличаются друг от друга в два раза. Считая, что рассеяние происходит на свободных электронах, найти длину волны падающего излучения.
7Фотон с энергией 1 МэВ рассеялся на свободном покоившемся электроне. Найти кинетическую энергию электрона отдачи, если в результате рассеяния длина волны фотона изменилась на 25%.
8В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол θ=90°. Энергия рассеянного фотона равна 0,4 МэВ. Определить энергию фотона до рассеяния.
9Фотон с энергией 0,75 МэВ рассеялся на свободном электроне под углом θ=60°. Принимая, что кинетическая энергия и импульс электрона до соударения с фотоном были пренебрежимо малы, определить: а) энергию рассеянного фотона; б) кинетическую энергию электрона отдачи; в) направление его движения.
10При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния 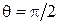 . Найти энергию и импульс рассеянного фотона.
. Найти энергию и импульс рассеянного фотона.
Ответы
1. 10. 2.  . 3.
. 3.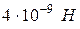 ;
; 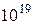 . 4.
. 4.  ;
; 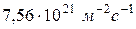 . 5.
. 5.  ;
;  . 6.
. 6.  . 7.
. 7. 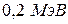 . 8.
. 8. 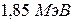 9.
9. 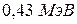 ;
;  ;
;  . 10.
. 10. 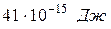 ;
; 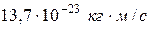 .
.
Волновые свойства микрочастиц
Вопросы:
· Гипотеза де Бройля.
· Соотношение де Бройля для энергии и импульса частицы.
· Соотношение неопределённостей Гейзенберга.
· Интерференция и дифракция микрочастиц.
Принятые обозначения:
· 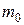 − масса покоя.
− масса покоя.
·  – неопределённость координат.
– неопределённость координат.
· 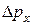 – неопределённость проекции импульса на ось x.
– неопределённость проекции импульса на ось x.
· 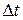 – время пребывания системы в определённом состоянии.
– время пребывания системы в определённом состоянии.
· 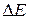 – неопределённость энергии в данном квантовом состоянии.
– неопределённость энергии в данном квантовом состоянии.
· 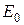 – энергия покоя.
– энергия покоя.
·  − межплоскостное расстояние в кристаллах.
− межплоскостное расстояние в кристаллах.
Основные формулы:
· Соотношение де Бройля для энергии движущейся частицы:
 .
.
· Формула де Бройля, связывающая длину волны с импульсом движущейся частицы:
а) если V << c, то 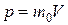 , а тогда
, а тогда 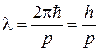 ;
;
б) если V ~ c, то 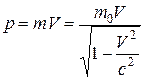 , а тогда
, а тогда 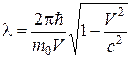 .
.
· Связь длины волны де Бройля с кинетической энергией частицы Wкин:
а) если V << c, то 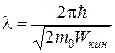 ;
;
б) если V ~ c, то 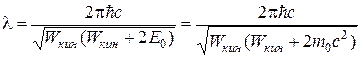 .
.
· Соотношение неопределённостей Гейзенберга:
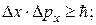
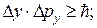
 и
и
 .
.
· Условие дифракционного максимума при отражении электронов от кристалла (формула Вульфа-Брэгга):
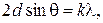
где 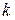 − порядок дифракции,
− порядок дифракции,  − угол отражения.
− угол отражения.
Задачи
1Найти длину волны де Бройля для: а) электрона, движущегося со скоростью 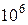 м/с; б) атома водорода, движущегося со средней квадратичной скоростью при температуре 300 К; в) шарика массой 1 г, движущегося со скоростью V = 1 см/с.
м/с; б) атома водорода, движущегося со средней квадратичной скоростью при температуре 300 К; в) шарика массой 1 г, движущегося со скоростью V = 1 см/с.
2α-частица движется по окружности радиусом r = 8,3 мм в однородном магнитном поле, напряженность которого Н = 18,9 кА/м. Найти длину волны де Бройля для α-частицы.
3 Частица движется слева направо в одномерном потенциальном поле, показанном на рисунке 1. Левее барьера, высота которого U = 15 эВ, кинетическая энергия частицы Т = 20 эВ. Во сколько раз и как изменится дебройлевская длина волны частицы при переходе через барьер.
Частица движется слева направо в одномерном потенциальном поле, показанном на рисунке 1. Левее барьера, высота которого U = 15 эВ, кинетическая энергия частицы Т = 20 эВ. Во сколько раз и как изменится дебройлевская длина волны частицы при переходе через барьер.
4Какую энергию необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 100 пм до 50 пм.
5Параллельный пучок моноэнергетических электронов падает на диафрагму с узкой прямоугольной щелью ширины 1,0 мкм. Определить скорость этих электронов, если на экране, отстающем от щели на расстояние 50 см, ширина центрального дифракционного максимума 0,36 мм.
6Пучок электронов с кинетической энергией 10 кэВ проходит через тонкую поликристаллическую фольгу и образует систему дифракционных колец на экране, отстоящем от фольги на 10 см. Найти межплоскостное расстояние, для которого максимум отражения третьего порядка соответствует кольцу с радиусом 1,6 см.
7Частица массы 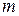 находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы
находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы 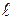 . Найти возможные значения энергии частицы, имея в виду, что реализуются лишь такие состояния ее движения, для которых в пределах данной ямы укладывается целое число дебройлевских полуволн.
. Найти возможные значения энергии частицы, имея в виду, что реализуются лишь такие состояния ее движения, для которых в пределах данной ямы укладывается целое число дебройлевских полуволн.
8Оценить наименьшие ошибки, с которыми можно определить скорость электрона, протона и шарика массы 1 мг, если координаты частиц и центра шарика установлены с неопределенностью 1 мкм.
9Показать, что для частицы, неопределенность местоположения которой 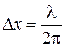 , где
, где  − ее дебройлевская длина волны, неопределенность скорости равна по порядку величины самой скорости частицы.
− ее дебройлевская длина волны, неопределенность скорости равна по порядку величины самой скорости частицы.
10Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы 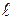 . Оценить с помощью соотношения неопределенностей силу давления электрона на стенки этой ямы при минимально возможной eго энергии.
. Оценить с помощью соотношения неопределенностей силу давления электрона на стенки этой ямы при минимально возможной eго энергии.
11Частица массы 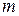 движется в одномерном потенциальном поле U =
движется в одномерном потенциальном поле U = 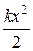 (гармонический осциллятор). Оценить с помощью соотношения неопределенностей минимально возможную энергию частицы в таком поле.
(гармонический осциллятор). Оценить с помощью соотношения неопределенностей минимально возможную энергию частицы в таком поле.
Ответы
1. 730 10-12 м; 145 10-12 м; 6,6 10-29 м. 2. 10,5 пм. 3. увеличится в 2 раза. 4. 0,45 кэВ. 5. 2 Мм/с. 6. 2,3  . 7.
. 7.  . 8. 100 м/с; 0,1 м/с; 10-22 м/с. 9.
. 8. 100 м/с; 0,1 м/с; 10-22 м/с. 9. 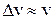 . 10.
. 10. 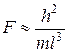 . 11.
. 11. 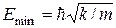 .
.
Квантово-механические операторы
Вопросы:
1 Линейные операторы.
2 Коммутативные операторы.
3 Самосопряжённые (эрмитовы) операторы.
4 Основные квантово-механические операторы.
Принятые обозначения:
·  – произвольная функция.
– произвольная функция.
·  − оператор импульса.
− оператор импульса.
·  − операторы проекции импульса на оси координат.
− операторы проекции импульса на оси координат.
·  − оператор полной энергии.
− оператор полной энергии.
·  – потенциальная энергия.
– потенциальная энергия.
· 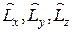 − операторы проекций момента импульса на оси координат.
− операторы проекций момента импульса на оси координат.
· 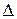 − оператор Лапласа.
− оператор Лапласа.
Основные формулы:
· Оператор 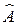 линейный, если:
линейный, если:
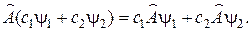
· Операторы 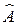 и
и коммутативны, если их коммутатор:
коммутативны, если их коммутатор:
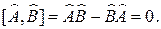
· Оператор 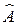 эрмитов (самосопряжённый), если:
эрмитов (самосопряжённый), если:
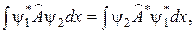
где 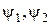 − произвольные функции.
− произвольные функции.
· Оператор проекции и квадрата импульса:
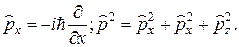
· Оператор полной энергии (гамильтониан):
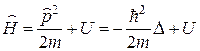 .
.
· Оператор проекции момента импульса:

· Оператор квадрата момента импульса:
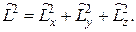
Задачи
1Проверить следующее операторное равенство: 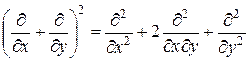 .
.
2Найти результат действия операторов 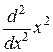 и
и 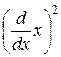 на функции: a)
на функции: a) 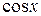 и б)
и б) .
.
3Найти собственное значение оператора 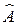
 , принадлежащее собственной функции
, принадлежащее собственной функции 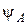 , если:
, если:
а) 
б) 
в) 
4Найти собственные функции 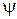 и собственные значения следующих операторов:
и собственные значения следующих операторов:
а) 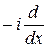 , если
, если 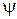 (x)=
(x)= 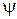 (x+a), а – постоянная;
(x+a), а – постоянная;
б)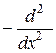 , если
, если 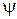 =0 при x=0 и x=
=0 при x=0 и x=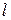 .
.
5Проверить следующие правила коммутации:
а) 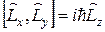
б) 
в) 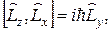
если известно: 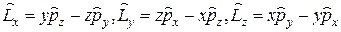 и
и 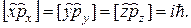
6С помощью правил коммутации, приведенных в предыдущей задаче, показать, что:
а) оператор 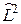 коммутирует с операторами
коммутирует с операторами 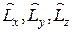
б) 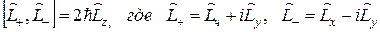 .
.
Ответы
2. 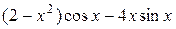 ;
; 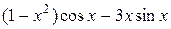 ;
;  ;
; 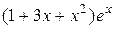 . 3. 4; 1;
. 3. 4; 1; 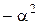 . 4.
. 4. 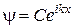 , где
, где 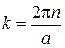 ,
, 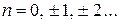 ;
;  , где
, где  ,
, 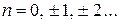
Уравнение Шредингера
Вопросы:
1 Временное уравнение Шредингера.
2 Стационарное уравнение Шредингера
3 Уравнение Шредингера в операторной форме
4 Стандартные условия, накладываемые на волновую функцию.
Принятые обозначения:
· 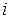 – мнимая единица,
– мнимая единица, 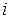 =
=
· 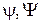 − волновая функция, описывающая состояние частицы.
− волновая функция, описывающая состояние частицы.
· 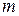 − масса частицы.
− масса частицы.
· 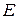 – полная энергия частицы.
– полная энергия частицы.
·  – потенциальная функция координат и времени.
– потенциальная функция координат и времени.
·  − постоянная Планка.
− постоянная Планка.
·  − оператор Лапласа.
− оператор Лапласа.
·  – вероятность.
– вероятность.
· 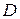 – коэффициент прозрачности.
– коэффициент прозрачности.
Основные формулы:
· Временное уравнение Шредингера:
 .
.
· Стационарное уравнение Шредингера:
 ,
,
если потенциал 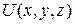 не зависит от времени.
не зависит от времени.
· Вероятность обнаружить частицу в интервале от x1 до x2:
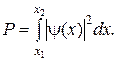
· Оператор Лапласа в сферических координатах для функции 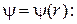
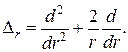
· Коэффициент прозрачности прямоугольного потенциального барьера конечной ширины:
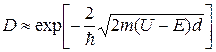 ,
,
где  – высота потенциального барьера,
– высота потенциального барьера,  − ширина барьера.
− ширина барьера.
Задачи
1Написать уравнение Шредингера для: а) электрона, находящегося в водородоподобном атоме; б) линейного гармонического осциллятора.
2Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины 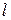 с абсолютно непроницаемыми стенками
с абсолютно непроницаемыми стенками  . Найти вероятность пребывания частицы в области
. Найти вероятность пребывания частицы в области 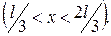 .
.
3Электрон наводится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы такова, что энергетические уровни расположены весьма густо. Найти плотность уровней 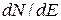 , т.е. их число на единичный интервал энергии, в зависимости от
, т.е. их число на единичный интервал энергии, в зависимости от 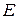 . Вычислить
. Вычислить 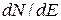 для
для 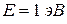 , если ширина ямы равна 1 см.
, если ширина ямы равна 1 см.
4Электрон находится в одномерном потенциальном ящике шириной 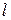 . Определить среднее значение координаты
. Определить среднее значение координаты  электрона, если
электрона, если 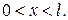
5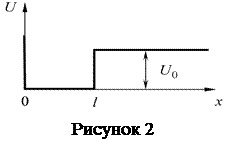 Частица массы
Частица массы 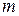 находится в одномерном потенциальном поле
находится в одномерном потенциальном поле 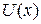 , вид которого показан на рисунке 2, где
, вид которого показан на рисунке 2, где  . Найти:
. Найти:
а) уравнение, определяющее возможные значения энергии частицы в области 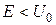 , привести это уравнение к виду:
, привести это уравнение к виду: 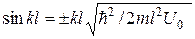 , где
, где 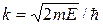 . Показать с помощью графического решения этого уравнения, что возможные значения энергии частицы образуют дискретный спектр;
. Показать с помощью графического решения этого уравнения, что возможные значения энергии частицы образуют дискретный спектр;
б) минимальное значение энергии  , при котором появляется первый энергетический ypoвeнь в области
, при котором появляется первый энергетический ypoвeнь в области 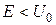 . При каком минимальном значении
. При каком минимальном значении  появляется n-ый уровень?
появляется n-ый уровень?
6Волновая функция частицы массы 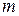 для основного состояния в одномерном потенциальном поле
для основного состояния в одномерном потенциальном поле 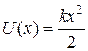 имеет вид
имеет вид  , где
, где 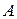 − нормировочный коэффициент,
− нормировочный коэффициент, 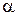 − положительная постоянная. Найти с помощью уравнения Шредингера постоянную
− положительная постоянная. Найти с помощью уравнения Шредингера постоянную 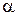 и энергию частицы
и энергию частицы 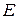 в этом состоянии.
в этом состоянии.
7Определить энергию электрона атома водорода в стационарном состоянии, для которого волновая функция 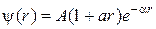 , где
, где 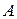 ,
, 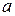 и
и 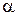 − некоторые постоянные.
− некоторые постоянные.
8Волновая функция электрона в основном состоянии атома водорода имеет вид 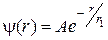 , где
, где 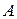 − некоторая постоянная, а
− некоторая постоянная, а  − первый боровский радиус. Найти:
− первый боровский радиус. Найти:
а) наиболее вероятное расстояние между электроном и ядром; 6) среднее значение модуля кулоновской силы; в) среднее значение потенциальной энергии электрона в поле ядра.
9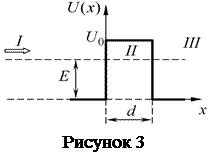 Электрон с энергией
Электрон с энергией 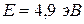 движется в положительном направлении оси
движется в положительном направлении оси  (смотри рисунок 3). Высота U потенциального барьера равна 5 эВ. При какой ширине d барьера вероятность
(смотри рисунок 3). Высота U потенциального барьера равна 5 эВ. При какой ширине d барьера вероятность  прохождения электрона через него будет равна 0,2?
прохождения электрона через него будет равна 0,2?
Ответы
2. 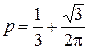 . 3. 0,8 107 уров/эВ. 4.
. 3. 0,8 107 уров/эВ. 4. 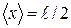 . 5. б)
. 5. б) 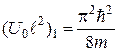 . 6.
. 6. 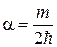 ;
;  7.
7. 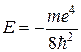 . 8. rвф=r1;
. 8. rвф=r1; 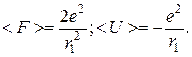 9. » 0,5 нм.
9. » 0,5 нм.
Спектры водородоподобных атомов
Вопросы:
1 Строение атома водорода и водородоподобных атомов.
2 Схема уровней в энергетическом спектре атома водорода.
3 Серии спектральных линий атома водорода и соответствующие им области шкалы электромагнитных волн.
4 Зависимость энергии квантовых состояний атома водорода от главного квантового числа.
5 Формула Бальмера.
Принятые обозначения:
· 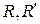 – постоянная Ридберга..
– постоянная Ридберга..
·  – главное квантовое число,
– главное квантовое число,  =1,2,3,…,
=1,2,3,…,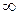 .
.
· 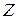 − зарядовое число.
− зарядовое число.
Основные формулы:
· Формула Бальмера для атома водорода:

где  − длина волны, излучаемая при переходе между уровнями с главными квантовыми числами
− длина волны, излучаемая при переходе между уровнями с главными квантовыми числами  и
и  ,
, 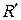 – постоянная Ридберга для атома водорода.
– постоянная Ридберга для атома водорода.
· Обобщенная формула Бальмера:
 ,
,
где  − постоянная Ридберга,
− постоянная Ридберга, 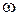 − циклическая частота спектральной линии.
− циклическая частота спектральной линии.
· Формулы, связывающие длину волны, частоту и циклическую частоту 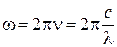 .
.
Задачи
1Сколько спектральных линий будет испускать атомарный водород, который возбуждают на  -ый энергетический уровень?
-ый энергетический уровень?
2Найти наименьшую 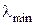 и наибольшую
и наибольшую  длины волн спектральных линий водорода в видимой области спектра.
длины волн спектральных линий водорода в видимой области спектра.
3Какие линии содержит спектр поглощения атомарного водорода в диапазоне длин волн от 94,5 до 130 нм?
4Какую наименьшую энергию  (в электронвольтах) должны иметь электроны, чтобы при возбуждении атомов водорода ударами этих электронов появились все линии всех серии спектра водорода? Какую наименьшую скорость
(в электронвольтах) должны иметь электроны, чтобы при возбуждении атомов водорода ударами этих электронов появились все линии всех серии спектра водорода? Какую наименьшую скорость  должны иметь эти электроны?
должны иметь эти электроны?
5В каких пределах должны лежать длины волн l монохроматического света, чтобы при возбуждении атома водорода квантами этого света наблюдались три спектральные линии?
6На дифракционную решетку нормально падает пучок света от разрядной трубки, наполненной атомарным водородом. Постоянная решетки  = 5 мкм. Какому переходу электрона соответствует спектральная линия, наблюдаемая при помощи этой решетки в спектре пятого порядка под углом j = 41°?
= 5 мкм. Какому переходу электрона соответствует спектральная линия, наблюдаемая при помощи этой решетки в спектре пятого порядка под углом j = 41°?
7Вычислить постоянную Ридберга, если известно, что для ионов 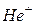 , разность длин волн между головными линиями серии Бальмера и Лаймана составляет 133,7 нм.
, разность длин волн между головными линиями серии Бальмера и Лаймана составляет 133,7 нм.
8Найти длину волны головной линии той спектральной серии ионов 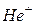 , у которой интервал между крайними линиями
, у которой интервал между крайними линиями 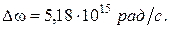
9Энергия связи электрона в основном состоянии атома гелия равна  . Найти энергию, необходимую для удаления обоих электронов из этого атома.
. Найти энергию, необходимую для удаления обоих электронов из этого атома.
10Покоившийся атом водорода испустил фотон, соответствующий головной линии серии Лаймана. Какую скорость приобрел атом?
11Покоящийся ион 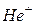 испустил фотон, соответствующий головной линии серии Лаймана. Этот фотон вырвал фотоэлектрон из покоящегося атома водорода, который находился в основном состоянии. Найти скорость фотоэлектрона.
испустил фотон, соответствующий головной линии серии Лаймана. Этот фотон вырвал фотоэлектрон из покоящегося атома водорода, который находился в основном состоянии. Найти скорость фотоэлектрона.
Ответы
1.  где n = 1, 2, 3,… 2. 365 нм; 656 нм. 3. 121,6 нм; 102,6 нм; 97,3 нм. 4. 13,6 эВ; 2,2 Мм/с. 5. (102,3¸121,5) нм. 6. n1=2, n2=3. 7. 2,07 1016 1/c. 8. 0,47 мкм. 9. 7,9 эВ. 10. 6 км/с. 11.3,1 106 м/с.
где n = 1, 2, 3,… 2. 365 нм; 656 нм. 3. 121,6 нм; 102,6 нм; 97,3 нм. 4. 13,6 эВ; 2,2 Мм/с. 5. (102,3¸121,5) нм. 6. n1=2, n2=3. 7. 2,07 1016 1/c. 8. 0,47 мкм. 9. 7,9 эВ. 10. 6 км/с. 11.3,1 106 м/с.
Свойства атомов
Вопросы:
1 Принцип Паули.
2 Связь периодичности структуры электронных оболочек атомов с периодической таблицей элементов Менделеева.
3 Электронные слои атомов и их обозначения.
4 Термы атомов и их обозначения.
5 Квантовые числа: главное, орбитальное, магнитное, спиновое и полного момента.
6 Механические моменты атома.
7 Правила отбора при излучении атомов.
8 Правила Хунда.
Принятые обозначения:
·  – главное квантовое число.
– главное квантовое число.
·  – орбитальное квантовое число.
– орбитальное квантовое число.
· 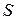 – спиновое квантовое число.
– спиновое квантовое число.
· 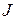 – внутреннее квантовое число.
– внутреннее квантовое число.
· 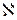 − мультиплетность.
− мультиплетность.
·  – орбитальный, спиновой и полный механический моменты.
– орбитальный, спиновой и полный механический моменты.
Основные формулы:
· Спектральные обозначения термов:
 ,
,
где  – буквенный символ орбитального квантового числа L=0,1,2,3,4,5,6,…(n-1), а соответствующий буквенный символ:
– буквенный символ орбитального квантового числа L=0,1,2,3,4,5,6,…(n-1), а соответствующий буквенный символ: 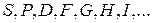 .
.
· Орбитальный механический момент атома:
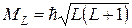 .
.
· Спиновой механический момент атома:
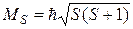 .
.
· Полный механический момент атома:
 .
.
· Мультиплетность:  .
.
· Правила отбора для квантовых чисел 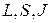 :
:
· 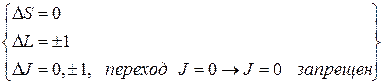 .
.
· Правила Хунда:
а) наименьшей энергией обладает терм с максимальным значением спинового квантового числа 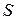 при данной электронной конфигурации;
при данной электронной конфигурации;
б) орбитальное квантовое число  при этом значении
при этом значении 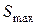 должно быть наибольшим;
должно быть наибольшим;
в) внутреннее квантовое число 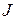 для основного состояния вычисляется по формуле
для основного состояния вычисляется по формуле 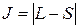 , если подоболочка заполнена не более, чем наполовину, и по формуле
, если подоболочка заполнена не более, чем наполовину, и по формуле  , если подоболочка заполнена более, чем наполовину.
, если подоболочка заполнена более, чем наполовину.
Задачи
1Выписать спектральные о6означения термов атома водорода, электрон которого наводится в состоянии с главным квантовым числом n=3.
2Найти возможные значения полных механических моментов атомов, находящихся в состояниях: а) 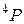 и б)
и б)  .
.
3Выписать спектральные символы термов двухэлектронной системы, состоящей из одного 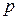 -электрона и одного
-электрона и одного  -электрона.
-электрона.
4Найти возможные мультиплетности 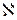 термов типа:
термов типа: 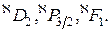
5Некоторый атом, кроме заполненных оболочек, имеет три электрона 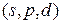 и находится в состоянии с максимально возможным для этой конфигурации полным механическим моментом. Найти в соответствующей векторной модели атома угол между спиновым и полным механическим моментом данного атома.
и находится в состоянии с максимально возможным для этой конфигурации полным механическим моментом. Найти в соответствующей векторной модели атома угол между спиновым и полным механическим моментом данного атома.
6Сколько различных типов термов возможно у двухэлектронной системы, состоящей из  и
и 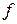 -электронов?
-электронов?
7Найти угол между спиновым и полным механическими моментами в векторной модели атома, содержащего кроме заполненных подоболочек три электрона 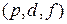 и имеющего максимально возможный для этой конфигурации полный механический момент.
и имеющего максимально возможный для этой конфигурации полный механический момент.
8Найти с помощью правил Хунда полный механический момент атома в основном состоянии, если его незаполненная подоболочка содержит: а) три d-электрона; б) семь d-электронов.
9Воспользовавшись правилами Хунда, найти число электронов в единственной незаполненной подоболочке атома, основной терм которого: а) 3F2; б) 2P3/2; в)6S5/2;
10Установить, какие из нижеперечисленных переходов запрещены правилами отбора: 2 D3/2  2Р1/2 , 2Р1
2Р1/2 , 2Р1  2S1/2 , 3F3
2S1/2 , 3F3  3Р2 , 4F7/2
3Р2 , 4F7/2  4D5/2.
4D5/2.
Ответы
1.  2.
2. 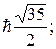
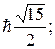
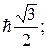
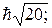
 3. 1P1; 3P0,1,2; 1D2; 3D1,2,3; 1F3; 3F2,3,4. 4. 1, 3, 5, 7, 9; 2, 4, 6; 3, 7, 9. 5. 31o. 6. 1P1, 1D2, 1F3, 1G4, 1H5, 3P0,1,2, 3F2,3,4, 3G3,4,5, 3H4,5,6. 7. 34,4o 8.
3. 1P1; 3P0,1,2; 1D2; 3D1,2,3; 1F3; 3F2,3,4. 4. 1, 3, 5, 7, 9; 2, 4, 6; 3, 7, 9. 5. 31o. 6. 1P1, 1D2, 1F3, 1G4, 1H5, 3P0,1,2, 3F2,3,4, 3G3,4,5, 3H4,5,6. 7. 34,4o 8. 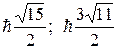 . 9. 2d – электрона; 5p – электронов; 5d – электронов. 10. 2-й и 3-й переходы.
. 9. 2d – электрона; 5p – электронов; 5d – электронов. 10. 2-й и 3-й переходы.
Магнитные свойства атомов. Эффект Зеемана
Вопросы:
1 Магнитные моменты электронов и атомов.
2 Магнетон Бора.
3 Квантование магнитных моментов.
4 Аномальный (сложный) эффект Зеемана.
5 Нормальный (простой) эффект Зеемана.
6 Правила отбора квантовых чисел.
Принятые обозначения:
·  − магнитный момент атома.
− магнитный момент атома.
·  − магнетон Бора.
− магнетон Бора.
· 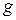 – фактор (множитель) Ланде.
– фактор (множитель) Ланде.
· 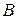 – индукция магнитного поля.
– индукция магнитного поля.
· 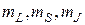 – магнитные орбитальные, магнитные спиновые и магнитные внутренние квантовые числа.
– магнитные орбитальные, магнитные спиновые и магнитные внутренние квантовые числа.
Основные формулы:
· Магнитон Бора:
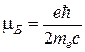 .
.
· Магнитный момент атома:
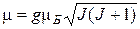 .
.
· Множитель (фактор) Ланде:
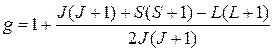 .
.
· Зеемановское расщепление спектральных линий:
 .
.
· Правила отбора квантовых чисел:
 ,
,
если  , то переход
, то переход  не осуществляется.
не осуществляется.
· Проекция магнитного момента атома на направление магнитного поля 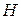 :
:

 Задачи
Задачи
1Валентный электрон атома натрия находится в состоянии с главным квантовым числом  =3, имея при этом максимально возможным полный механический момент. Каков его магнитный момент в этом состоянии?
=3, имея при этом максимально возможным полный механический момент. Каков его магнитный момент в этом состоянии?
2Определить возможные значения магнитного момента атома в состоянии 4Р.
3Максимальное значение проекции магнитного момента атома, находящегося в состоянии D2, равно четырем магнетонам Бора. Определить мультиплетность этого терма.
4Вычислить с помощью правил Хунда магнитный момент основного состояния атома, в котором незаполненная подоболочка имеет электронную конфигурацию:
а) 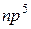 ; б)
; б) .
.
5Найти полный механический момент атома в состоянии с S = 3/2 и L = 2, если известно, что магнитный момент его равен нулю.
6Атом водорода в нормальном состоянии находится на расстоянии r = 2,5 см от длинного прямого провода с током I = 10 А. Найти силу, действующую на атом.
7Атом в состоянии 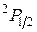 находится на оси кругового контура с током
находится на оси кругового контура с током 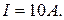 . Расстояние между атомом и центром контура с током
. Расстояние между атомом и центром контура с током 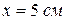 , радиус контура
, радиус контура  . Вычислить максимальное значение силы взаимодействия между атомом и этим током.
. Вычислить максимальное значение силы взаимодействия между атомом и этим током.
8На сколько подуровней расщепится в слабом магнитной поле терм: а) 3Р0; б) 2F5/2; в) 4D1/2.
9Определить спектральный символ терма атома, если полная ширина расщепления этого терма в слабом магнитном поле с индукцией  составляет
составляет 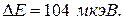
10Изо6разить схему возможных переходов в сла6ом магнитном поле между термами 2Р3/2 и 2S1/2. Вычислить для магнитного поля 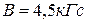 смещение (в рад/с) зеемановских компонент этой линии.
смещение (в рад/с) зеемановских компонент этой линии.
11Изобразить схему возможных переходов в слабом магнитном поле и вычислить смещения (в единицах  ) зеемановских компонент спектральной линии:
) зеемановских компонент спектральной линии:
а)  ; б)
; б) 
Ответы
1. 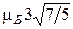 . 2.
. 2. 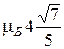 ;
;  ;
;  . 3. 7. 4.
. 3. 7. 4.  ;
;  . 5.
. 5.  . 6. 3 10-26 Н. 7. 4,1 10-27 Н. 8. 0, 6, 0. 9. 1F3; 10.
. 6. 3 10-26 Н. 7. 4,1 10-27 Н. 8. 0, 6, 0. 9. 1F3; 10. 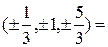
 . 11.
. 11. 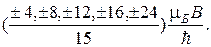
Основные характеристики ядер
Вопросы:
1 Состав и характеристики атомного ядра.
2 Модели атомного ядра.
3 Ядерные силы.
4 Дефект массы и энергия связи ядра.
Принятые обозначения:
· 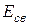 − энергия связи ядра.
− энергия связи ядра.
· 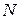 – число нейтронов в ядре.
– число нейтронов в ядре.
· 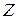 – зарядовое число.
– зарядовое число.
· 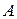 – массовое число.
– массовое число.
·  – массы нейтрона, протона и соответствующего атома.
– массы нейтрона, протона и соответствующего атома.
· 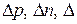 − избыток массы протона, нейтрона и атома
− избыток массы протона, нейтрона и атома
Основные формулы:
· Радиус ядра с массовым числом 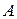 :
:
 ферми.
ферми.
· Энергия связи ядра (в единицах массы):
 или
или
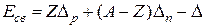 .
.
· Массовое число:
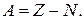
· Удельная энергия связи:
 .
.
Задачи
1Оценить плотность ядерного вещества, концентрацию нуклонов и объемную плотность электрического заряда в ядре.
2Найти с помощью формулы 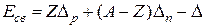 : а) энергию связи ядра, которое имеет одинаковое число протонов и нейтронов, а радиус в полтора раза меньший радиуса ядра 27Al; б) энергию связи на один нуклон в ядрах 6Li, 40Ar, 107Аg и 208РЬ.
: а) энергию связи ядра, которое имеет одинаковое число протонов и нейтронов, а радиус в полтора раза меньший радиуса ядра 27Al; б) энергию связи на один нуклон в ядрах 6Li, 40Ar, 107Аg и 208РЬ.
3Определить: а) энергию связи нейтрона и 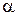 -частицы в ядре 21Ne; б) энергию, необходимую для разделения ядра 16О на четыре одинаковые частицы.
-частицы в ядре 21Ne; б) энергию, необходимую для разделения ядра 16О на четыре одинаковые частицы.
4Найти энергию возбуждения ядра 207Рb, возникающего при захвате ядром 206Рb медленного нейтрона.
5Вычислить энергию связи нейтрона в ядре 14N, если известно, что энергии связи ядер 14N и 13N равны 104,66 и 94,10 МэВ.
6Найти энергию, необходимую для разделения ядра 16О на 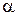 -частицу и ядро 12С, если известно, что энергии связи ядер 16О, 12С и 4Не равны 127,62; 92,16 и 28,30 МэВ.
-частицу и ядро 12С, если известно, что энергии связи ядер 16О, 12С и 4Не равны 127,62; 92,16 и 28,30 МэВ.
7Определить энергию, выделяющуюся при образовании двух 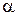 -частиц в результате синтеза ядер 2Н и 6Li, если известно, что энергии связи на один нуклон в ядрах 2Н, 4Не и 6Li равны соответственно 1,11; 7,08 и 5,33 МэВ.
-частиц в результате синтеза ядер 2Н и 6Li, если известно, что энергии связи на один нуклон в ядрах 2Н, 4Не и 6Li равны соответственно 1,11; 7,08 и 5,33 МэВ.
8Показать, что при равномерном распределении заряда по объему ядра энергия кулоновского отталкивания протонов 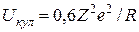 , где
, где 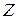 и
и 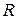 − заряд и радиус ядра.
− заряд и радиус ядра.
9Вычислить разность энергий связи зеркальных ядер 33S и 33Cl, если известно, что масса атома 33S меньше массы атома 33Cl на 0,00599 а.е.м. Сравнить полученную величину с разностью энергий кулоновского отталкивания протонов в этих ядрах (см. формулу из предыдущей задачи). Объяснить причину совпадения результатов.
Ответы
1. 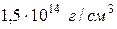 ;
;  ;
; 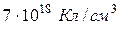 . 2. а) 18Ве;
. 2. а) 18Ве;  ; б)
; б)  ;
; 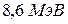 ;
; 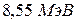 ;
; 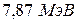 . 3. а)
. 3. а)  и
и 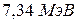 ; б)
; б) 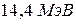 . 4.
. 4. 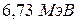 . 5.
. 5. 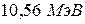 . 6.
. 6. 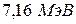 . 7.
. 7.  . 9.
. 9.  ,
,  . Совпадение объясняется приблизительным равенством ядерных сил между нуклонами.
. Совпадение объясняется приблизительным равенством ядерных сил между нуклонами.
Радиоактивность. Ядерные реакции
Вопросы:
1 Радиоактивные превращения ядер.
2 Характеристики ядерных реакций.
3 Законы радиоактивного распада.
4 a и b-распады.
5 g-излучение и его свойства.
Принятые обозначения:
· 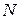 – число ядер данного типа.
– число ядер данного типа.
·  – убыль числа ядер за время
– убыль числа ядер за время 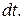
·  − постоянная радиоактивного распада.
− постоянная радиоактивного распада.
· 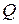 – активность радиоактивного изотопа.
– активность радиоактивного изотопа.
· 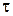 − среднее время жизни радиоактивных ядер.
− среднее время жизни радиоактивных ядер.
·  – период полураспада.
– период полураспада.
Основные формулы:
· Основной закон радиоактивного распада:
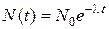 , где
, где  − начальное число ядер.
− начальное число ядер.
· Постоянная радиоактивного распада:
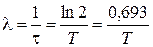 .
.
· Период полураспада:
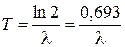 .
.
· Среднее время жизни радиоактивных ядер:
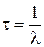 .
.
· Активность радиоактивного изотопа:
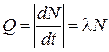 .
.
· Удельная активность:

Задачи
1Какая доля первоначального количества ядер  : а) останется через 10 и 100 лет; б) распадется за одни сутки; за 15 лет?
: а) останется через 10 и 100 лет; б) распадется за одни сутки; за 15 лет?
2Вычислить постоянную распада, среднее время жизни и период полураспада радиоактивного изотопа, активность которого уменьшается в 1,07 раза за 100 дней.
3Найти постоянную распада l радона, если известно, что число атомов радона уменьшается за сутки на 18,2%.
4Найти удельную активность 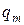 : а) урана
: а) урана  ; 6) радона
; 6) радона 
5Некоторый радиоактивный изотоп имеет постоянную распада 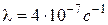 . Через какое время распадется 75% первоначальной массы атомов?
. Через какое время распадется 75% первоначальной массы атомов?
6Распад ядер 210Ро происходит из основного состояния и сопровождается испусканием двух групп 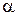 -частиц: основной с энергией 5,30 МэВ и слабой по интенсивности с энергией 4,50 МэВ. Найти энергию
-частиц: основной с энергией 5,30 МэВ и слабой по интенсивности с энергией 4,50 МэВ. Найти энергию 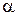 -распада этих ядер и энергию
-распада этих ядер и энергию 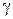 -квантов, испускаемых дочерними ядрами.
-квантов, испускаемых дочерними ядрами.
7Вычислить суммарную кинетическую энергию частиц, возникающих при  -распаде покоящегося нейтрона.
-распаде покоящегося нейтрона.
8Нейтрон испытал упругое соударение с первоначально покоившимся дейтроном. Определить долю кинетической энергии, теряемую нейтроном: а) при лобовом соударении; б) при рассеянии под прямым углом.
9Написать недостающие обозначения 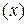 в следующих ядерных реакциях:
в следующих ядерных реакциях:
а)  ;
;
б) 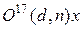 ;
;
в)  ;
;
г) 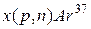 .
.
Ответы
1. а) 0,78 и 0,084; б) 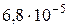 и 0,31. 2.
и 0,31. 2. 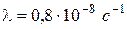 ;
;  ;
;  . 3.
. 3.  . 4.
. 4. 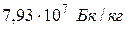 ;
; 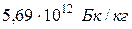 . 5.
. 5.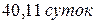 . 6. 5,4 и
. 6. 5,4 и 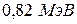 . 7.
. 7. 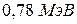 . 8.
. 8. 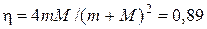 ;
; 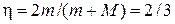 , где
, где 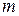 и
и 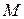 − массы нейтрона и дейтрона. 9. а)
− массы нейтрона и дейтрона. 9. а)  ; б) 17F; в)
; б) 17F; в) 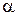 ; г) 37Cl
; г) 37Cl
Основные физические постоянные
Некоторые астрономические величины
Таблица свойств некоторых изотопов
| Z, заряд | Изотоп | Избыток массы атома, а.е.м. | Тип распада | Период полураспада |
| n | 0,008665 | 
| 11,7 мин | |
| 1H | 0,007825 | |||
| 2H | 0,014102 | |||
| 3H | 0,016049 | 
| 12,3 года | |
| 4He | 0,002604 | |||
| 6Li | 0,015126 | |||
| 8Be | 0,005308 | 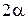
|  c c
| |
| 10B | 0,012939 | |||
| 12C | ||||
| 14N | 0,003074 | |||
| 16O | -0,005085 | |||
| 17O | -0,000867 | |||
| 18F | 0,000950 | 
| 1,87 час | |
| 20Ne | -0,007560 | |||
| 21Ne | -0,006151 | |||
| 23Na | -0,010227 | |||
| 33S | -0,028540 | |||
| 37Cl | -0,034104 | |||
| 37Ar | -0,033228 | K | 32 дня | |
| 40Ar | -0,037616 | |||
| 90Sr | -0,09223 | 
| 28 лет | |
| 107Ag | -0,09303 | |||
| 206Pb | -0,02554 | |||
| 207Pb | -0,02410 | |||
| 208Pb | -0,02336 | |||
| 210Po | -0,01713 | 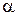
| 138 дней | |
| 222Rn | 0,01753 | 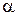
| 3,8 дня | |
| 235U | 0,04393 | 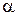
| 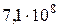 лет лет
|
Учебное издание
КВАНТОВАЯ МЕХАНИКА
АТОМНАЯ ФИЗИКА И СПЕКТРОСКОПИЯ
ЭЛЕМЕНТЫ ЯДЕРНОЙ ФИЗИКИ
Задачи для аудиторной и самостоятельной работы
Составители: Китаева Елена Алексеевна,
Макарян Владимир Георгиевич
Стукалина Ирина Леонидовна
Самарский государственный аэрокосмический университет имени академика С.П. Королева
443086, Самара, Московское шоссе, 34
– Конец работы –
Используемые теги: Квантовая, Механика, Атомная, Физика, спектроскопия, Элементы, ядерной, физики0.103
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: КВАНТОВАЯ МЕХАНИКА АТОМНАЯ ФИЗИКА И СПЕКТРОСКОПИЯ ЭЛЕМЕНТЫ ЯДЕРНОЙ ФИЗИКИ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов