В данной теме мы начнем изучение квантовых закономерностей явлений природы
АТОМНАЯ ФИЗИКА (12)
Введение
В конце ХIX в. даже у крупных ученых сложилось представление, что в физике уже все изучено и объяснено, что все физические законы открыты и остается только рутинная работа по доработке теорий, уточнению формулировок, разработке вычислительных методик, а в целом здание физики как науки уже выстроено. Оставались не объясненными несколько вопросов, на которые надеялись получить ответы в ближайшем будущем. К ним относились отрицательный результат опыта Майкельсона, распределение энергии в спектре излучения абсолютно черного тела, закономерности фотоэффекта, сериальные закономерности спектров атомов, поведение теплоемкостей различных тел при изменении температуры, нарушения закона Дюлонга и Пти, связывающего электропроводность и теплопроводность твердых тел при изменении температуры.
Решение первой из указанных проблем привело к созданию Эйнштейном теории относительности, а решение второй проблемы, данное Планком, послужило толчком к созданию квантовой механики, объяснившей все остальные указанные проблемы.
Эти два направления в физике составляют содержание новейшей физики - физики XX-го столетия, которая выяснила, что все законы природы имеют приближенный характер и справедливы только при выполнении определенных условий.
В данной теме мы начнем изучение квантовых закономерностей явлений природы.
Принципиальная сложность при изучении квантовой физики заключается в том, что классические понятия, выработанные наукой при изучении макроскопических явлений совершенно непригодны в области микромира, то есть для явлений, происходящих с электронами, атомами и другими малыми частицами вещества.
Равновесное тепловое излучение
1. В проблеме теплового излучения большое значение имеет понятие равновесного излучения. Чтобы представить, что это такое, рассмотрим замкнутую… Опыт показывает, что через некоторый промежуток времени рассматриваемая… Атомы и молекулы тела и стенок при столкновениях дают излучение, которое перемещается в полости, перенося энергию.…Стоячие волны в трехмерном пространстве.
Формула Релея-Джинса
, где волновые числа определяются граничными условиями . Первое условие выполняется автоматически для данной функции, описывающей распределение амплитуды вдоль струны. Из…Понятие вероятности. Средние значения случайных величин
1. Большинство физических величин изменяется хаотически, т.е. являются случайными величинами. Различают дискретные и непрерывные случайные величины.… Пусть произведено измерений дискретной случайной величины, при этом раз… .Понятие о квантах. Средняя энергия осциллятора. Фотоны
1. Формирование электромагнитного поля равновесного излучения является случайным процессом, так как случайны процессы испускания света телами.… По классическим представлениям энергия любой системы может изменяться на… .Модели атома Томсона и Резерфорда
В 1903 году Томсон предложил первую модель строения атома, называемую моделью пудинга. Согласно этой модели атом представляет собой равномерно… Внутри равномерно заряженного шара с объемной плотностью , где - заряд шара, -… ,Столкновение заряженных частиц
Учитывая взаимодействие -частицы только с ядром, к которому -частица подходит наиболее близко мы приходим к задаче столкновения двух заряженных… Предположим, что -частица имея импульс , направленный вдоль прямой…Формула Резерфорда и ее экспериментальная проверка
Представим, что параллельный пучок -частиц от радиоактивного источника Р площадью поперечного сечения падает на тонкую металлическую фольгу Ф… Прицельный параметр ,Спектры излучения атомов.
В 1885 году швейцарский физик Бальмер, изучая спектр излучения атомов водорода, обнаружил, что длины волн четырех спектральных линий в видимой… , , гдеПостулаты Бора
Первый закон, сформулированный Бором в виде постулата, утверждает: атом может находиться длительное время в стационарных состояниях, которые… Второй постулат также является важнейшим законом квантовой физики. При… . (4)Опыты Франка и Герца
Опыты Франка и Герца начались до появления теории Бора и имели целью определение потенциалов ионизации. Но эти опыты принесли экспериментальное… В этих опытах через исследуемый газ проходили электроны ускоренные… Если бы в колбе поддерживался вакуум, то зависимость тока от ускоряющего напряжения была бы такой же, как в вакуумном…Принцип соответствия. Правило квантования
По классическим представлениям, механическая энергия электрона, движущегося по круговой орбите вокруг ядра с зарядом , складывается из кинетической… . При этом первое слагаемое, в силу второго закона НьютонаТеория Бора для водородоподобных атомов.
Спектр излучения атома водорода
и правило квантованияОрбитальный магнитный момент
Магнитный момент кругового тока по определению равен . Учитывая, что , выражение для магнитного момента перепишем в виде . Сравнивая это выражение с формулой момента импульса . нетрудно заметить, чтоГипотеза де-Бройля. Волны де Бройля.
Пусть частица вещества движется в свободном пространстве со скоростью u. Де Бройль предположил, что с такой частицей связана некоторая плоская… , (1) распространяющаяся в направлении скорости u. О физическом смысле этой волны де Бройль ничего сказать не мог. Такие…Дифракция микрочастиц. Опыты Дэвиссона и Джермера
Пучок электронов с одинаковыми энергиями из электронной пушки ЭП направлялся на монокристалл никеля Ni. Исследовалось рассеивание электронов… В этих опытах для анализа дифракционной картины использовался метод Брэгга,… Отражение рентгеновских лучей от атомных плоскостей кристалла носит интерференционный характер. От различных…Опыты Тартаковского и Томсона, опыты Фабриканта и Штерна
В методе Дебая электронный пучок направлялся на металлическую фольгу (Работы Томсона и Тартаковского). На фотопластинке, поставленной за фольгой,… Поликристаллическая фольга состоит из множества маленьких кристалликов,… .Особенности поведения микрочастиц
С точки зрения здравого смысла поведение микрочастиц кажется парадоксальным. Представить объект, обладающий корпускулярно-волновым дуализмом… Наиболее выпукло парадоксальность поведения микрочастиц проявляется при… Если пропускать микрочастицы через верхнюю щель, то на экране появляется достаточно широкое плавное распределение…Соотношения неопределенностей
Действительно, задание координат и импульса материальной точки в какой то момент времени позволяет рассчитать ее состояние в любой другой момент и… Отсутствие траектории у микрочастицы свидетельствует о том, что она не имеет одновременно точных значений координат и…Дифракция микрочастиц на щели
Пусть движение электрона описывается плоской волной де Бройля. Электрон в этом случае обладает вполне определенным значением импульса. Например .… При падении плоской волны на щель шириной а мы можем принять за величину… При дифракции на щели в области Фраунгофера возникает дифракционное поле с распределением интенсивностиПределы применимости классической механики
1. Соотношения неопределенностей Гейзенберга для координат и импульсов отражают тот факт, что в природе объективно не существует состояний микрочастиц с точно определенными значениями координат и импульсов.
В частном случае неопределенности импульса может и не быть (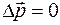 ). Так будет, например, в случае плоской монохроматической волны де Бройля. Но в этом случае, согласно неравенствам Гейзенберга неопределенности координат обращаются в бесконечность
). Так будет, например, в случае плоской монохроматической волны де Бройля. Но в этом случае, согласно неравенствам Гейзенберга неопределенности координат обращаются в бесконечность  , и о месте, где локализована микрочастица, ничего сказать нельзя. Она может быть с одинаковой вероятностью обнаружена в любой точке пространства. (Плоская волна имеет бесконечную протяженность, как по фронту, так и вдоль направления распространения).
, и о месте, где локализована микрочастица, ничего сказать нельзя. Она может быть с одинаковой вероятностью обнаружена в любой точке пространства. (Плоская волна имеет бесконечную протяженность, как по фронту, так и вдоль направления распространения).
При локализации микрочастицы в какой-то точке пространства неопределенности координат исчезают, а неопределенности импульсов возрастают до бесконечности, т.е. все значения импульса становятся равновероятными.
Соотношения неопределенностей определяют принципиальный предел неточности координат и сопряженных им проекций импульса, с которыми состояние частицы можно описывать классически и рассчитывать их траектории.
2. Обратимся к числовым оценкам, вытекающим из принципа неопределенности Гейзенберга. Будем считать его универсальным законом природы и рассмотрим, в каких случаях квантовые неопределенности в координатах и импульсах можно не учитывать.
Рассмотрим движение макроскопического тела с массой 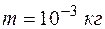 . Пусть неопределенность в определении ее положения Dz составляет
. Пусть неопределенность в определении ее положения Dz составляет 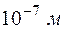 , тогда неопределенность импульса
, тогда неопределенность импульса
 .
.
Отсюда неопределенность в возможных значениях скорости
 .
.
Данные неопределенности настолько малы, что всегда заведомо меньше погрешности измерения. В этом случае мы можем при движении частицы не учитывать ее волновых свойств и считать ее классической.
Отступления от классического движения из-за принципа неопределенности лежат далеко за пределами возможностей эксперимента.
Рассмотрим теперь движение электрона в электронно-лучевой трубке. Скорость электронов по порядку величины составляет uz = 107м/с.
Если считать неопределенность значений скорости лежащей в пределах 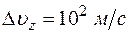 , что составляет
, что составляет 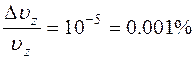 , то неопределенность в координате
, то неопределенность в координате 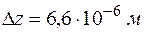 . В этом случае также погрешности измерения скорости и координат превышают квантовые неопределенности и движение электрона можно считать классическим.
. В этом случае также погрешности измерения скорости и координат превышают квантовые неопределенности и движение электрона можно считать классическим.
Совсем иначе обстоит дело с движением электрона в атоме. Возьмем атом водорода и первую боровскую орбиту. Правило квантования орбит по Бору

означает, что на круговой орбите укладывается целое количество длин волн де Бройля
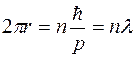
и
 .
.
Теперь если мы зададимся столь большой неопределенностью в положении орбиты, что  , то
, то
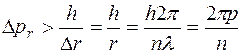 .
.
Для первой боровской орбиты неопределенность в импульсе превысит величину самого импульса.
В этом случае представление о движении электрона по классическим орбитам теряет смысл. Неопределенности в координатах и импульсе столь велики, что движение является безтраекторным. В лучшем случае, понятием траектории можно пользоваться для высоких энергетических состояний (большие n).
Минимальная энергия и размеры атома
Деление энергии на кинетическую и потенциальную теряет смысл, поскольку нет определенных значений скорости и расстояния r. Принцип неопределенности позволяет объяснить тот факт, что электрон не падает… Точное положение электрона в атоме запрещено принципом неопределенности: был бы бесконечно большой разброс в его…Оператор координаты и проекции импульса
1. Уравнения квантовой механики записываются в операторном виде. Оператор это закодированный некоторым символом алгоритм действий над функцией. Как правило, для обозначения операторов над буквенным символом используется шляпка. В результате действия оператора 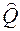 на функцию
на функцию 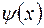 получается новая функция
получается новая функция 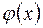
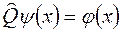 .
.
Если функция 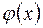 пропорциональна
пропорциональна 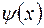 , и коэффициент пропорциональности является физической величиной Q
, и коэффициент пропорциональности является физической величиной Q

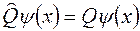 , (1)
, (1)
то оператор 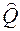 является оператором физической величины Q. Функция
является оператором физической величины Q. Функция 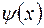 называется собственной функцией, а численное значение величины Q –собственным значением оператора
называется собственной функцией, а численное значение величины Q –собственным значением оператора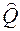 или уравнения (1).
или уравнения (1).
2. Для того чтобы установить вид операторов, используемых в квантовой механике, рассмотрим плоскую волну де Бройля, соответствующую свободному движению микрочастицы
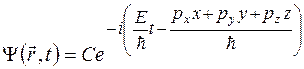 . (2)
. (2)
Продифференцируем выражение (2) по координате и умножим результат на ( ).В результате получим уравнение
).В результате получим уравнение
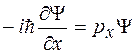 .(3)
.(3)
где 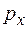 является проекцией импульса на ось x, а оператор, стоящий перед волновой функцией в левой части уравнения называется оператором проекции импульса на ось x
является проекцией импульса на ось x, а оператор, стоящий перед волновой функцией в левой части уравнения называется оператором проекции импульса на ось x
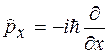 . (4)
. (4)
Уравнение (3) показывает, что волновая функция (2) является собственной функцией оператора проекции импульса на ось x.
Общим решением уравнения (6) является функция
 , (5)
, (5)
в которой С может учитывать зависимость волновой функции от других переменных.
Аналогично можно получить операторы для двух других проекций
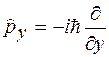 ,
,  .
.
Собственные функции этих операторов имеют вид
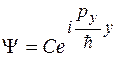 ,
,  .
.
3. Кроме рассмотренных операторов в квантовой механике используется оператор координаты 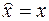 , действие которого на волновую функцию сводится просто к умножению ее на величину x. Точно также оператором скалярной функции координат является сама скалярная функция
, действие которого на волновую функцию сводится просто к умножению ее на величину x. Точно также оператором скалярной функции координат является сама скалярная функция 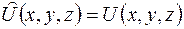 .
.
Сложение и умножение операторов
1. Операторы можно складывать и умножать. Оператором суммы двух операторов 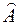 и
и  называется такой оператор
называется такой оператор 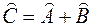 , действие которого на функцию
, действие которого на функцию  , равно сумме результатов действия на нее операторов
, равно сумме результатов действия на нее операторов 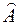 и
и 
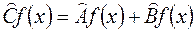 .
.
Если операторы 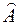 и
и  имеют собственные функции и собственные значения, удовлетворяющие уравнениям
имеют собственные функции и собственные значения, удовлетворяющие уравнениям
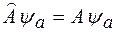 ,
, 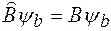 , (7)
, (7)
причем операторы 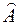 и
и  действуют только на свои собственные функции, т.е
действуют только на свои собственные функции, т.е
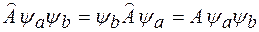 и
и  , (8)
, (8)
тогда оператор
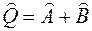 (9)
(9)
имеет собственные значения, равные сумме собственных значений операторов 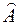 и
и 
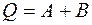 , (10)
, (10)
и собственные функции, равные произведению собственных функций операторов 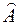 и
и 
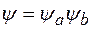 , (11)
, (11)
удовлетворяющие уравнению
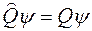 .(12)
.(12)
Для доказательства этого утверждения подставим (11) в (12) и учтем (8) и (10)
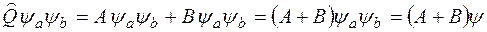 .
.
Таким образом, функции (11) являются собственными функциями уравнения (12) по определению (1), а собственные значения оператора 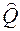 равны сумме собственных значений операторов
равны сумме собственных значений операторов 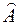 и
и  .
.
Не все операторы коммутируют. Так, например, операторы  и
и  не коммутируют, так как
не коммутируют, так как
 ,
,
 ,
,
поэтому
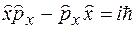 . (13)
. (13)
Если операторы 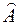 и
и  не коммутируют, то точных значений величин A и B одновременно не существует. Поэтому операторное равенство (18) неразрывно связано с соотношением неопределенности для координаты и соответствующей проекции импульса.
не коммутируют, то точных значений величин A и B одновременно не существует. Поэтому операторное равенство (18) неразрывно связано с соотношением неопределенности для координаты и соответствующей проекции импульса.
Операторы физических величин
1. Мы установили операторы координаты и проекции импульса. Все остальные операторы вводятся следующим образом. Всякой классической величине 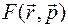 соответствует оператор
соответствует оператор 
 , получающийся заменой классических величин
, получающийся заменой классических величин  и
и 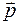 на соответствующие операторы
на соответствующие операторы 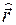 и
и 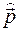 .
.
Например: для оператора импульса

оператор имеет вид
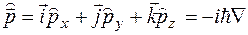 ,
,
а волновая функция будет равна произведению волновых функций
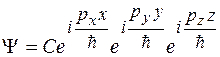 ,
,
и собственное значение – сумме собственных значений операторов проекций, умноженных на соответствующие орты
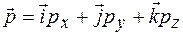 .
.
2. Пользуясь произведением операторов, можем написать выражение для оператора квадрата проекции импульса на ось x
 .
.
Оператор квадрата проекции импульса на ось x представляет собой вторую производную по координате x, умноженную на 
 . (14)
. (14)
Аналогично записываются операторы для квадратов проекций на другие оси координат
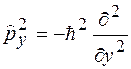 ,
,  . (15)
. (15)
Прямой проверкой можно убедиться в том, что собственные функции оператора проекции импульса являются собственными функциями оператора 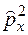 , т.е. уравнения
, т.е. уравнения
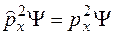 .
.
Действительно, учитывая уравнение для собственных функций оператора проекции импульса  , получаем
, получаем  .
.
Отсюда следует, что волновая функция свободной микрочастицы является собственной функцией оператора квадрата проекции импульса на ось x.
3. Из этих операторов можно составить оператор
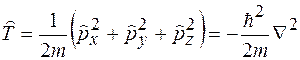 . (16)
. (16)
Если этим оператором подействовать на волновую функцию (2), то получим
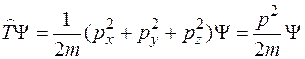 . (17)
. (17)
Так как величина 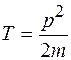 является кинетической энергией, то оператор
является кинетической энергией, то оператор 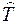 является оператором кинетической энергии, и волновая функция (2) является собственной функцией оператора
является оператором кинетической энергии, и волновая функция (2) является собственной функцией оператора 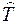 .
.
Временное уравнение Шредингера
соответствует равномерному свободному движению частицы в определенном… Уравнение Шредингера должно быть общим для всех движений. Поэтому уравнение не должно содержать параметров, выделяющих…Стационарные состояния. Свойства волновых функций
, где w - постоянная, а не зависит от времени. В стационарных состояниях плотность вероятностиПотенциальный барьер. Решение стационарного уравнения
Рассмотрим простейшую ситуацию, когда направления налетающих и рассеянных частиц параллельны оси . В этом случае… Такой барьер описывается потенциальной функциейКоэффициенты отражения и пропускания ступенчатого барьера
4. При оба волновых числа являются действительными, поэтому все три волны однородны. Наличие отраженной волны приводит к конечной вероятности… Плотность вероятности равна квадрату модуля волновой функции . Если умножить…Туннельный эффект
Используя граничные условия при х = 0 и х = L, можно найти все величины: r, а, b, d и подсчитать коэффициент пропускания барьера. В результате можно получить =.Микрочастица в одномерной прямоугольной потенциальной яме
, (84) . Общее решение такого уравнения содержит две произвольные постоянные A и BТрехмерная потенциальная яма. Яма конечной глубины
, то есть уравнение ,Система двух взаимодействующих частиц
При квантовомеханическом анализе системы из двух микрочастиц мы будем считать, что гамильтониан системы складывается из операторов кинетической… , . Через , обозначены координаты рассматриваемых микрочастиц.Модель гармонического осциллятора
Для малых колебаний достаточно ограничиться первыми двумя членами. Кроме того,… ,Собственные значения и собственные функции
Одномерного гармонического осциллятора
, (1) где , . (2)Момент импульса
. В квантовой механике не существует состояния, в котором оба вектора и имеют… .Собственные функции и собственные значения оператора
Проекции момента импульса
. Это обыкновенное дифференциальное уравнение первого порядка. Его решение можно… .Собственные значения оператора углового момента
Собственные значения  и собственные функции
и собственные функции 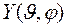 оператора квадрата момента импульса находятся путем решения соответствующего операторного уравнения
оператора квадрата момента импульса находятся путем решения соответствующего операторного уравнения
 .
.
Но собственные значения  можно определить с помощью одних только правил коммутации. Приведем эти правила к более удобному для этой цели виду, введя два оператора
можно определить с помощью одних только правил коммутации. Приведем эти правила к более удобному для этой цели виду, введя два оператора
 ,
, 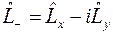 .
.
Простой проверкой можно убедиться в справедливости соотношений
 ,
, 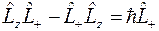 ,
, 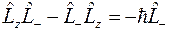 .
.
Далее, вычисляя оператор квадрата углового момента, получим
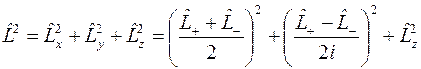 ,
,
или
 .
.
Рассмотрим состояние, в котором проекция углового момента на ось z принимает наибольшее значение
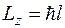 .
.
В этом состоянии
 ,
, 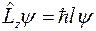 .
.
Из соотношений коммутации для такой функции получим
 .
.
Отсюда следует, что функции  и
и 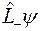 являются собственными функциями оператора
являются собственными функциями оператора  , имеющими собственные значения
, имеющими собственные значения  и
и 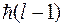 , соответственно. Но величина
, соответственно. Но величина  не может быть собственным значением оператора
не может быть собственным значением оператора  , так как по предположению наибольшим собственным значением этого оператора является
, так как по предположению наибольшим собственным значением этого оператора является 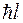 .
.
Таким образом, равенство

невозможно, хотя оно логически вытекает из соотношений коммутации и уравнения 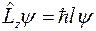 .
.
Избежать противоречия можно только в том случае, если 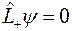 . Но отсюда следует
. Но отсюда следует  и
и
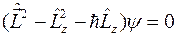 .
.
Но в силу того, что 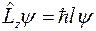 и
и 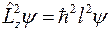 , получим
, получим
 .
.
Следовательно, собственные значения оператора углового момента равны
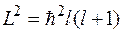 .
.
Квантовое число 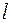 называется орбитальным квантовым числом и принимает положительные целочисленные значения 0, 1, 2, … .
называется орбитальным квантовым числом и принимает положительные целочисленные значения 0, 1, 2, … .
 |
Состояния микрочастицы с заданным значением квадрата углового момента
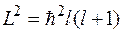 могут иметь различные проекции углового момента на выделенное направление, в которых магнитное квантовое число может принимать
могут иметь различные проекции углового момента на выделенное направление, в которых магнитное квантовое число может принимать  значений:
значений:  . Данные результаты, определяющие возможные значения
. Данные результаты, определяющие возможные значения 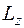 и
и  , называют пространственным квантованием.
, называют пространственным квантованием.
Для наглядности пространственное квантование обычно представляют на векторных диаграммах. По оси z откладывают возможные значения m, рассматривая их как проекции вектора 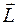 длины
длины 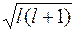 , имеющего дискретные направления в пространстве. Эти диаграммы не следует понимать буквально. (Вектор углового момента в квантовой механике принципиально не имеет определенных направлений в пространстве.) Они правильно передают только два факта: возможные значения проекции m и возможные значения квадрата углового момента
, имеющего дискретные направления в пространстве. Эти диаграммы не следует понимать буквально. (Вектор углового момента в квантовой механике принципиально не имеет определенных направлений в пространстве.) Они правильно передают только два факта: возможные значения проекции m и возможные значения квадрата углового момента  .
.
В классической механике кинетическая энергия вращающегося тела определяется формулой
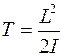 ,
,
где  - момент инерции тела относительно соответствующей оси вращения. Такая же формула справедлива и в квантовой механике. Различие состоит в том, что величина
- момент инерции тела относительно соответствующей оси вращения. Такая же формула справедлива и в квантовой механике. Различие состоит в том, что величина 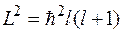 принимает дискретные значения.
принимает дискретные значения.
Неизменяемая вращающаяся система в квантовой механике называется ротатором. Таким образом, энергетические уровни ротатора дискретны и определяются формулой
 .
.
Для некоторых целей вращающуюся молекулу можно рассматривать как жесткий ротатор, и пользоваться этой формулой, если изменения l , связанные с вращением, не велики.
Собственные функции оператора квадрата момента импульса
Уравнение для определения собственных функций и собственных значений оператора 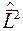 имеет вид
имеет вид
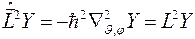 .
.
Введя обозначение
 ,
,
и записывая оператор Лапласа на сфере в явном виде, получим дифференциальное уравнение в частных производных
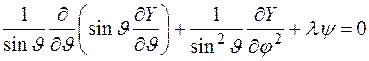 . (1)
. (1)
Уравнение необходимо решить для всей области координат на сфере ( ,
, 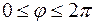 ). Поэтому собственные функции оператора квадрата момента импульса зависят только от угловых координат. Они называются сферическими функциями и используются в различных разделах физики (в акустике, электродинамике, метеорологии, и т.д.). Так как собственные функции операторов квадрата момента и проекции момента на ось
). Поэтому собственные функции оператора квадрата момента импульса зависят только от угловых координат. Они называются сферическими функциями и используются в различных разделах физики (в акустике, электродинамике, метеорологии, и т.д.). Так как собственные функции операторов квадрата момента и проекции момента на ось 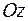 являются общими, то решение этого уравнения отыскивается методом разделения переменных, полагая
являются общими, то решение этого уравнения отыскивается методом разделения переменных, полагая
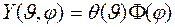 .
.
Подстановка этого решения в уравнение, приводит к выражению
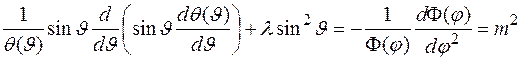
В этом выражении приравниваются функции, зависящие от разных аргументов, что возможно, если они равны постоянной величине, которую мы обозначили 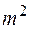 . В результате разделения переменных мы получили два обыкновенных дифференциальных уравнения
. В результате разделения переменных мы получили два обыкновенных дифференциальных уравнения
 , (2)
, (2)
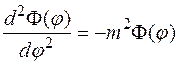 . (3)
. (3)
Волновая функция оператора проекции момента импульса удовлетворяет уравнению (3).
Уравнение (2) имеет непрерывные однозначные конечные решения только при строго определенных значениях параметра
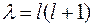 ,
, 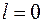 , 1, 2, 3, . . . .
, 1, 2, 3, . . . .
Это значит, что квадрат момента импульса принимает дискретный ряд значений
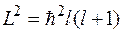 .
.
Отметим только, что решения уравнения (2) зависят от двух чисел 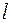 и
и  . Сделав замену переменной
. Сделав замену переменной 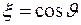 в уравнении, его решения представляют собой присоединенные полиномы Лежандра.
в уравнении, его решения представляют собой присоединенные полиномы Лежандра.
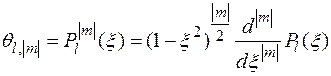 ,
,
где
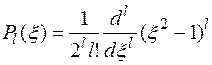
- полиномы Лежандра
Процедура решения уравнения (2) выходит за рамки курса общей физики. Поэтому мы ограничимся приведением сферических волновых функций  для нескольких небольших квантовых чисел
для нескольких небольших квантовых чисел
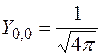 ,
,
 ,
,  ,
, 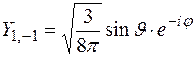 ,
,
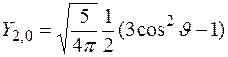 ,
, 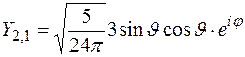 ,
, 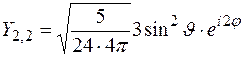 .
.
Сферические волновые функции позволяют определить вероятность того, что микрочастица (квазичастица), находящаяся в состоянии, описываемом волновой функцией 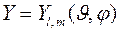 , будет находиться в элементе телесного угла
, будет находиться в элементе телесного угла
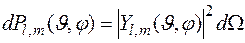 .
.
Поэтому эта вероятность не зависит от угла  . Это означает, что в плоскости, перпендикулярной оси
. Это означает, что в плоскости, перпендикулярной оси 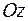 распределение вероятности имеет осевую симметрию.
распределение вероятности имеет осевую симметрию.
Угловое распределение вероятности зависит от квантовых чисел 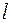 и
и  , т.е. от величины момента импульса и величины его проекции на ось
, т.е. от величины момента импульса и величины его проекции на ось 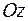 .
.
Состояние с 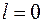 (
(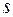 -состояние) обладает сферической симметрией распределения вероятности, так как
-состояние) обладает сферической симметрией распределения вероятности, так как  . Поэтому
. Поэтому
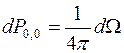 .
.
Такие состояния являются сферически симметричными и обозначаются буквой s.
Для l = 1 состояния с различными значениями магнитного квантового числа имеют различную направленность в угловом распределении плотности вероятности. Такие состояния обозначаются буквой p.
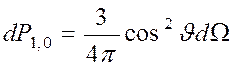 ,
,  .
.
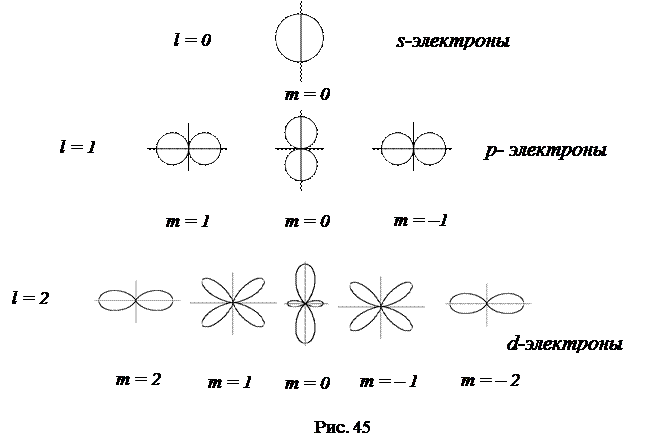
Для l =2 число состояний увеличивается до пяти и направленность электронных облаков увеличивается (лепестки распределений сужаются).
 ,
, 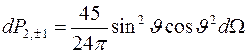 ,
,
 .
.
Соответствующие распределения угловой плотности вероятности показаны на рисунке.
Состояния с l =2,3,4,... обозначаются буквами d, f, g,.., соответственно.
Центральное силовое поле. Оператор Лапласа в сферических
Координатах
, то такое силовое поле называется центральным. Оно обладает сферической… Помимо силовой характеристики поля существует еще энергетическая характеристика – потенциальная энергия. В центральном…Спектр энергий в кулоновском поле
, уравнение (2) для электрона движущегося в кулоновском поле ядраРадиальные волновые функции в атоме водорода
Вероятность обнаружения электрона в шаровом слое между и определяется формулой . (4) Плотность радиального распределения вероятности обладает следующими особенностями.Сложение угловых моментов
Оператором углового момента системы частиц называют сумму операторов угловых моментов ее частей и : . Так же определяется и оператор проекции углового момента на избранное направление. Например,Спин электрона. Тонкая структура спектра излучения
Атома водорода.
В отсутствие магнитного поля на экране получалось четкое изображение щели. При включении сильно неоднородного магнитного поля на атомы действует… Если величина принимает любые значения (непрерывна), то при прохождении через магнитное поле полоска Р на экране…Принцип тождественности состояний неразличимых частиц.
Принцип Паули
Чтобы уяснить эти отличия будем рассматривать коллектив из двух микрочастиц (например, электронов). Отметим положения этих микрочастиц в некоторый… С классической точки зрения за дальнейшим движением таких частиц можно… Таким образом, по классическим законам одинаковые частицы индивидуализированы, т.е. принципиально различимы. Если…В системе однотипных микрочастиц реализуются только такие состояния, которые не меняются при перестановке местами двух любых микрочастиц.
. При этом оказывается, что возможны два типа волновых функций, описывающих… ,Особенности периодической системы элементов
Позднее исследования Резерфорда и Мозли показали, что атомный номер равен заряду ядра, измеренному в единицах элементарного заряда. Порядковый номер… Свойства атома определяются состоянием всей электронной оболочки атома и… Поскольку задача многих тел в квантовой механике сложна не менее, чем в классической, то отыскание точной волновой…Спин-орбитальное взаимодействие
Если перейти в систему отсчета, связанную с электроном, то в такой системе движется ядро со скоростью . Движущееся в такой системе ядро создает… , гдеЭнергетические уровни и спектральные серии щелочных металлов
При отсутствии валентного электрона распределение электрических зарядов в остове и его электрическое поле являются сферически симметричными. Наличие… . Здесь второе слагаемое представляет энергию взаимодействие валентного электрона с диполем.Результирующий механический момент атома
, величина которого определяется квантовым числом .Магнитный момент атома
, , для спинового момента , ,Эффект Зеемана. Классическое объяснение
В 1896 г. Зееман обнаружил, что если источник света помещен в магнитное поле, то спектральные линии расщепляются. При наблюдении поперек магнитного поля спектральная линия расщепляется на три линейно поляризованные компоненты. Средняя компонента не смещена и вектор 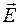 направлен параллельно магнитному полю (такие компоненты называются
направлен параллельно магнитному полю (такие компоненты называются  -компонентами).
-компонентами).
Две крайние компоненты с частотами  и
и 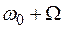 поляризованы перпендикулярно к нему (такие компоненты называются
поляризованы перпендикулярно к нему (такие компоненты называются  -компонентами).
-компонентами).
При наблюдении вдоль магнитного поля средняя компонента отсутствует, а две крайние поляризованы по кругу. Причем компонента с меньшей частотой поляризована по правому кругу, а с большей частотой – по левому кругу.
Частота
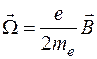
называется Ларморовой частотой прецессии электронных орбит, которая происходит по закону
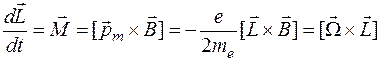 .
.
Лоренц дал этому явлению следующее объяснение. Излучателем световых волн является гармонический осциллятор, представляющий собой электрический диполь. Дипольный момент осциллятора можно разложить на две составляющие вдоль направления магнитного поля и перпендикулярно ему. Продольная составляющая дипольного момента не дает излучения вдоль этого направления. Она ответственна за появление линейно поляризованной  -компоненты. Поперечная составляющая дипольного момента ответственна за появление
-компоненты. Поперечная составляющая дипольного момента ответственна за появление  -компонент.
-компонент.
В отсутствие магнитного поля колебания этой составляющей дипольного момента можно разложить на два круговых вращения в плоскости xy с одной и той же угловой частотой 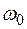 . При наблюдении вдоль магнитного поля они дают волны поляризованные по кругу, а при наблюдении поперек магнитного поля – линейно поляризованные волны.
. При наблюдении вдоль магнитного поля они дают волны поляризованные по кругу, а при наблюдении поперек магнитного поля – линейно поляризованные волны.
 При наложении магнитного поля возникает дополнительное вращение этой составляющей дипольного момента против часовой стрелки с ларморовой частотой, если смотреть в направление против направления магнитного поля.
При наложении магнитного поля возникает дополнительное вращение этой составляющей дипольного момента против часовой стрелки с ларморовой частотой, если смотреть в направление против направления магнитного поля.
Такое расщепление спектральных линий на три компоненты наблюдается в сильных магнитных полях и называется простым эффектом Зеемана. Простой эффект дают синглетные, т.е. одиночные спектральные линии. Подавляющее большинство спектральных линий являются мультиплетами, т.е. состоят из нескольких тесно расположенных спектральных линий. Мультиплеты в магнитном поле дают значительно более сложную картину расщепления. Такие расщепления называются сложным эффектом Зеемана.
Учет спина позволил полностью объяснить эффект Зеемана.