Стационарные состояния. Свойства волновых функций

Особое значение в квантовой механике имеют стационарные состояния. Это такие состояния, в которых все наблюдаемые физические параметры не меняются с течением времени. Сама волновая функция принципиально не наблюдаема, но с ее помощью определяются по определенным правилам значения физически наблюдаемых величин. Оказывается, что в стационарных состояниях

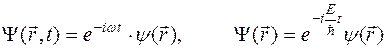где w - постоянная, а 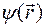не зависит от времени.

В стационарных состояниях плотность вероятности

от времени не зависит и является функцией только координат. Дифференцируя волновую функцию стационарных состояний по времени и подставляя результат в основное уравнение Шредингера запишем

Это уравнение не содержит времени и называется уравнением Шредингера для стационарных состояний.

Решения этого уравнения зависят от вида потенциальной функции 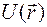и существуют, вообще говоря, не при любых значениях величины Е. Избранные значения параметра Е, для которых имеются решения уравнения, называются собственными значениями величины Е, и соответствующие им волновые функции называются собственными функциями этого уравнения. Собственные значения Е принимаются за возможные значения энергии в стационарных состояниях.

Собственные значения энергии могут быть дискретными (если ) и их можно пронумеровать в порядке возрастания Е₁, Е₂, Е₃, ..., а могут непрерывно заполнять конечный или бесконечный интервал (если Е < U()). В первом случае говорят, что энергетический спектр дискретный, а во втором - непрерывный.

Квантование энергии возникает потому, что на волновые функции, являющиеся решениями уравнения Шредингера, накладываются определенные естественные ограничения. Они заключаются в том, что волновая функция и ее первые производные должны быть конечны, однозначны и непрерывны даже в точках разрыва потенциальной функции . Эти требования получили название стандартных условий.

Требование однозначности волновой функции означает, что при обходе по любому замкнутому контуру (в том числе при обходе особых точек уравнения) волновая функция должна возвращаться к своему прежнему значению. В противном случае для одной и той же точки будут иметься две или больше вероятностей 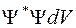, что лишено всякого физического смысла.

Требование конечности волновой функции обусловлено тем, что вероятность нахождения микрочастицы в окрестности любой точки пространства 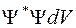должна быть конечной.

Требование непрерывности это естественное требование, предъявляемое к любой волновой функции (волна должна быть непрерывна в окрестности любой точки пространства).

Собственные функции должны удовлетворять условию нормировки

,

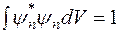Это означает, что вероятность обнаружения микрочастицы во всей области движения равна единице (вероятность достоверного события). Кроме того, волновые функции удовлетворяют условию ортогональности

,

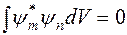которое означает, что интеграл от произведения различных волновых функций по всей области движения равен нулю.