Потенциальный барьер. Решение стационарного уравнения

1. Рассмотрим рассеяние микрочастиц на преграде, испускаемых источником, удаленным на большое расстояние от нее. Силовое воздействие на микрочастицу определяется потенциальной энергией взаимодействия этой преграды с микрочастицей.

Рассмотрим простейшую ситуацию, когда направления налетающих и рассеянных частиц параллельны оси 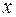. В этом случае протяженность преграды в направлении перпендикулярном оси 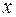можно считать бесконечно большой и рассматривать одномерное движение. При большой протяженности вдоль оси 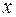, преграду можно считать бесконечно большой и моделировать ее ступенькой (прямоугольным барьером бесконечной протяженности).

Такой барьер описывается потенциальной функцией

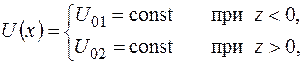
причем (рис. 1).

На границу барьера слева налетает частица, движущаяся со скоростью u.

Выбранная форма барьера указывает на то, что силы, действующие на частицу, существуют в бесконечно узком слое при х=0.

С классической точки зрения частица будет отражаться, не изменяя кинетической энергии, если ее полная энергия 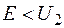, и будет продолжать движение в прежнем направлении, если , но с меньшей кинетической энергией.

На границу барьера слева налетает поток частиц, движущихся со скоростью u. Выбранная форма барьера указывает на то, что силы, действующие на частицу, существуют в бесконечно узком слое при х=0. Энергия таких частиц слева от барьера (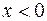) является чисто кинетической.

2. Квантовая механика дает совершенно другое решение. Состояние микрочастицы определяется волновой функцией, являющейся решением уравнения Шредингера для всей области движения (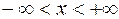), которая позволяет рассчитывать различные вероятности. Стационарное уравнение Шредингера в одномерном случае имеет вид

,

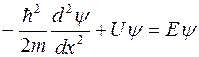которое мы запишем в форме

, (1)

где волновое число

(2)

зависит от разности полной энергии и потенциальной функции, которая различна по разные стороны барьера. Поэтому и волновые числа по разные стороны барьера будут разными; обозначим их

, .

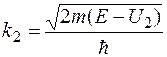Для отыскания волновой функции необходимо найти решения уравнения (1) в левой и правой областях. Будем искать их в виде

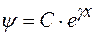. (3)

Подставив формулу (3) в (1) получим характеристическое уравнение

.

Его корни и приводят к двум частным решениям:

и ,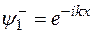

соответствующим волнам, идущим вдоль оси x и обратно.

Общее решение уравнения Шредингера для левой области (х < 0) записывается в виде

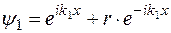. (4)

Здесь амплитуда падающей волны принята за единицу, а амплитуда отраженной волны обозначена r.

Общее решение уравнения Шредингера для правой области

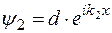(5)

содержит только одну прошедшую волну.

 

3. Амплитудные коэффициенты отраженной r и прошедшей d волн находятся из граничных условий. Волновая функция, описывающая любое состояние, должна быть непрерывна вместе с первой производной. Это требование сводится к выполнению уравнений

, и 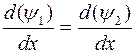при х = 0.

Из этих граничных условий получаются соотношения между амплитудными коэффициентам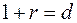и

и .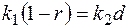

Из них находим

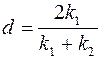, r = . (6)

Принципиальное отличие квантово-механического решения от классического состоит в том, что в классической физике частица локализована, а в квантовой механике - нет. В классической физике говорят об энергии и состоянии частицы, когда она находится в определенном месте пространства. В квантовой механике это не так. Решение, даваемое уравнением Шредингера, относится ко всему пространству. Падающая волна органически связана с прошедшей и отраженной волнами. Все три волны относятся к одному состоянию микрочастицы. Спектр собственных значений энергии является сплошным.