Координатах
1. Если силы, действующие на частицу в разных точках пространства, направлены вдоль прямых, проходящих через одну и ту же точку, называемую центром, и зависят только от расстояния до него
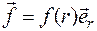 ,
,
то такое силовое поле называется центральным. Оно обладает сферической симметрией.
Помимо силовой характеристики поля существует еще энергетическая характеристика – потенциальная энергия. В центральном поле она зависит только от 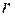
 .
.
Законы движения в поле центральной силы образуют фундамент атомной физики. Решение общей задачи о движении электронов в атоме опирается в той или иной мере на результаты движения одной квазичастицы с приведенной массой 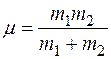 в силовом поле
в силовом поле  относительно неподвижного центра масс. Для системы электрон – ядро (в атоме водорода или в водородоподобных ионах),
относительно неподвижного центра масс. Для системы электрон – ядро (в атоме водорода или в водородоподобных ионах), 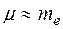 . Поэтому упрощенно можно считать, что квазичастица тождественна электрону, движущемуся возле неподвижного тяжелого ядра в силовом поле (в кулоновском поле).
. Поэтому упрощенно можно считать, что квазичастица тождественна электрону, движущемуся возле неподвижного тяжелого ядра в силовом поле (в кулоновском поле).
Частным случаем центрального поля является кулоновское поле в водородоподобных атомах
 .
.
В общем случае в центральном поле зависимость потенциальной энергии от 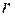 является более сложной, чем в кулоновском поле.
является более сложной, чем в кулоновском поле.
Замечательной особенностью центрального поля является сферическая симметрия энергии взаимодействия, т.е. ее независимость от угловых координат. Поэтому уравнения Шредингера для центрального взаимодействия проще всего решать в сферических координатах.
2. Оператор Лапласа в сферических координатах имеет вид
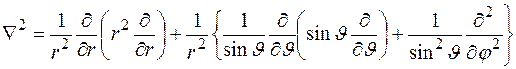 .
.
Выражение в фигурных скобках называется оператором Лапласа на сфере
 .
.
Таким образом, для оператора кинетической энергии  в сферических координатах получаем выражение
в сферических координатах получаем выражение
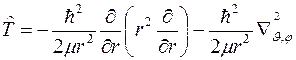 .
.
Оно состоит из двух слагаемых
 ,
,
где  есть оператор квадрата момента импульса, а
есть оператор квадрата момента импульса, а  есть
есть
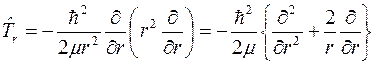 .
.
Оператор  может рассматриваться как оператор кинетической энергии, соответствующий радиальному движению, а оператор
может рассматриваться как оператор кинетической энергии, соответствующий радиальному движению, а оператор 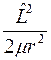 - как оператор кинетической энергии трансверсального движения.
- как оператор кинетической энергии трансверсального движения.
3. Задача заключается в нахождении стационарных состояний частицы, движущейся в поле  , т.е. в отыскании решений уравнения Шредингера для стационарных состояний
, т.е. в отыскании решений уравнения Шредингера для стационарных состояний
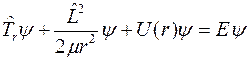 . (1)
. (1)
Так как операторы полной энергии 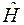 и квадрата момента импульса
и квадрата момента импульса  коммутируют, то волновые функции у них должны быть общими.
коммутируют, то волновые функции у них должны быть общими.
Если положить
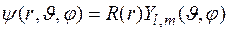 ,
,
то, во-первых, автоматически будет выполняться уравнение
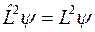 ,
,
во-вторых, учитывая, что собственные значения оператора  равны
равны
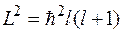
можно получить уравнение
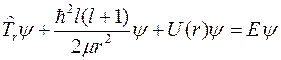 .
.
Это уравнение содержит явно только одну переменную 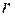 . Поделив его на
. Поделив его на  , получим уравнение для радиальной функции
, получим уравнение для радиальной функции 
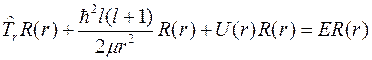 . (2)
. (2)
Его называют уравнением Шредингера для радиальной функции  .
.
Вид радиальной волновой функции определяется энергией взаимодействия  и потенциальной энергии электрона
и потенциальной энергии электрона 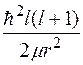 в поле центробежной силы. Следовательно, орбитальное квантовое число влияет на вид радиальной функции.
в поле центробежной силы. Следовательно, орбитальное квантовое число влияет на вид радиальной функции.
Возможные значения энергии определяются из уравнения (2) и зависят от вида  . Они могут зависеть от величины момента импульса (через
. Они могут зависеть от величины момента импульса (через 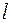 ), но не могут зависеть от проекции момента импульса
), но не могут зависеть от проекции момента импульса 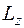 . Причиной этого является сферическая симметрия силового поля, когда все направления в пространстве равноправны, и поэтому энергия не может зависеть от ориентации в пространстве момента импульса.
. Причиной этого является сферическая симметрия силового поля, когда все направления в пространстве равноправны, и поэтому энергия не может зависеть от ориентации в пространстве момента импульса.