МЕТРОЛОГИЯ

 

С.В. Бирюков, А.И. Чередов

 

МЕТРОЛОГИЯ

 

Тексты лекций

 

Омск 2000

ББК 30.10 я 73 Б 64 Рецензенты:

МЕТРОЛОГИЯ. ОСНОВНЫЕ ПОНЯТИЯ В ОБЛАСТИ МЕТРОЛОГИИ

Метрология зародилась в глубокой древности и по словообразованию озна­чает учение о мерах. В первом русском труде по метрологии (Ф.И.Петрушевский.… Измеряемыми величи­нами, с которыми имеет дело метрология в настоящее время,… Метрология подразделяется на законодательную метрологию- раздел метрологии, включающий комплексы взаимосвязанных и…

Основные понятия и определения

Мет­рология является одной из областей науки и её роль за последние де­сятилетия чрезвычайно возросла. Метрология проникла и завоевала (или завоевывает) себе позиции во всех областях жизни и дея­тельности человечества. В силу этого обстоятельства метрологи­ческая терминология тесно соприкасается с терминологией каждой из «специальных сфер».

В нашей стране действует стандарт на терминологию ГОСТ 16263—70 «Государственная система обеспечения единства изме­рений. Метрология. Термины и определения» и закон об обеспечении единства измерений*, вводящий новые понятия и определения и уточняющий ранее действующие.

Далее в разделе рассматриваются некоторые основные поня­тия и относящиеся к ним термины и определения, нашедшие широ­кое применение и выходящее за рамки метрологии. Поэтому их рассмотрение нельзя отнести к какому-либо разделу метрологии. С другой стороны, многие из этих терминов именно в силу их ши­рокого распространения получают искаженное толкование, непра­вильно применяются или заменяются неправильными терминами. Не установив единства понимания и толкования таких общих терминов, практически невозможно излагать ни одного раздела метрологии.

 

Измерение. Измеряемые величины

Значение величины, найденное путем его измерения, называется результатом измере­ния. Значение величины, полученное при отдельном измерении,… В определение понятия метрологического обеспечения входит термин «единство… Этот термин позволяет обеспечить сопоставимость измерений, выпол­ненных в разное время, разными средствами и методами.…

Физическая величина. Единица физической величины

Индивидуальность в количественном отношении следует пони­мать в том смысле, что свойство может быть для одного объек­та в определенное число раз… Как правило, термин «величина» применяют в отношении свойств или их… В стандарте есть только термин «физическая величина», а сло­во «величина» дано как краткая форма основного термина,…

Системы единиц физических величин

В общем виде связь между производной величиной Z и основными мо­жет быть представлена следующим уравнением: Z = LaMbTgIeQhJl, где L, М, Т, I, Q, J — основные величины; a, b, g, e, h, l— показатели раз­мерности. Эта формула называется формулой…

Размер величины. Значение величины

Иногда возражают против широкого применения слова «размер», утверждая, что оно относится только к длине. Однако заметим, что каждое тело обладает… Часто в словосочетании «размер величины» слово «размер» опускают или за­меняют… В машиностроении широко применяют термин «размер», подразумевая под ним значение физической величины - длины,…

Размерность физических величин

Размерность физической величины обозначается dim A (от лат. dimension – размерность). Допустим, что физическая величина А связана с X, Y уравнением… Х = х×[Х]; Y = y×[Y]; A = а×[A], где А, X, Y - символы, обозначающие физическую вели­чину; а, х, y - числовые значения величин (безразмер­ные); [A];…

Измерительное преобразование

В некоторых случаях, когда нельзя непосредственно сравнить измеряемую величину с воспроизводимой единицей физической величины, используют измерительное преобразование. Это такой вид преобразования, при котором устанавливается однозначное соответствие между значениями двух величин (входной и выходной). Зависимость между этими величинами стремятся сделать линейной. Диапазон преобразования определяется множеством значений входной величины, подвергаемой преобразованию [1].

 

Вид измерений

Вид измерений - часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин. Например, в области электрических и магнитных измерений могут быть выделены как виды измерения электрического сопротивления, электродвижущей силы, электри­ческого напряжения, магнитной индукции и др.

 

Методы и средства измерений

Принцип измерений - это совокупность физических явлений, на которых основаны измерения. Например, измерение температуры с использованием… Конкретные методы измерений определяются видом измеряе­мых величин, их… Каждую физическую величину можно измерить несколькими методами, которые могут отличаться друг от друга особенностями…

Меры

Мера - средство измерений, предназначенное для воспроизве­дения

физической величины заданного размера.

Некоторые меры являются телами определенной формы, изго­товленными с необходимой тщательностью. Например, концевые меры длины, гири, измерительные колбы. Другие меры представ­ляют совокупность многих деталей с определенной взаимосвязью (нормальный элемент, измерительный конденсатор, генератор стандартных сигналов), но не это является характерным для мер и их роли в измерениях. Вспомним любой процесс измерения. Относительно редко сравнивают измеряемую величину с мерой, значение которой равно единице. На рычажных весах сравнивают массу взвешиваемого тела с массой гирь 0,1; 0,2; 0,5; 1; 2; 5 кг. Следовательно, любая из этих гирь или их комбинация в процес­се измерения может стать исходной для определения измеряемой массы. Таким образом, мера воспроизводит величины, значения которых связаны с принятой единицей этой величины определен­ным, известным соотношением. Мера - это, как правило, основа измерений [4].

 

Эталоны единиц физических величин. Образцовые средства

Измерений

Эталон единицы физической величины выполняется по особой спецификации и официально утверждается в установленном по­рядке. При конкретном применении… В технике, науке и даже в художественной литературе слово «эталон»… Сам по себе термин «образцовое средство измерений» допу­скает двоечтение. Он может быть ошибочно понят как лучшее…

Точность измерений

Под точностью измерения понимают степень при­ближения результатов измерений к истинному значению измеряе­мой величины. Однако выражения вроде…  

Погрешность измерений

Выше было сказано, что на практике истинное значение изме­ряемой величины мы заменяем более близким к нему значением, более точным, чем полученное… Действительное значение изме­ряемой величины - это значение, найденное… Погрешность результата измерения может быть выражена в единицах измеряемой величины или в долях (или в процентах) ее…

Поверка средств измерений

Неправильно поверку средств измерений называть «проверкой», так как слово «проверка» имеет иной смысл. Например, можно проверять выполнение… Сличение средств измерений — разновидность поверки, при выполнении которой… Калибровка меры или набора мер - поверка совокупности однозначных мер или одной многозначной меры на различных…

ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ

Прежде чем разбираться в сущности каких-либо явлений, удобно их сначала упорядочить, т.е. классифицировать.

Измерения подразделяются на виды измерений – часть области измерений,

имеющая свои особенности и отличающаяся однородностью измеряемых величин, и методы измерений - часть области измерений, состоящая в различии приемов использования принципов и средств измерений.

 

Классификация видов измерений

Классификацию видов измерений можно проводить по различным классификационным признакам, к которым можно отнести следующие: способ нахождения численного значения физической величины, число наблюдений, характер зависимости измеряемой величины от времени, число измеряемых мгновенных значений в заданном интервале времени, условия, определяющие точность результатов, способ выражения результатов измерения (рис. 2.1) [7].

По способу нахождения численного значения физической величины измерения подразделяются на следующие виды: прямые, косвенные, совокупные и совместные.

Прямым измерением называют измерение, при котором значение измеряемой физической величины находят непосредственно из опытных данных. Прямые измерения характеризуются тем, что эксперимент как процесс измерения производится над самой из­меряемом величиной, имея в виду то или

иное её проявление. Прямые измерения выполняются при помощи средств, предназначенных для измерения данных величин. Числовое значение измеряемой величины отсчитывается непосредственно по показанию измерительного прибора. средств, величин. Примеры прямых измерений: измерение тока ампер­метром; напряжения - компенсатором; массы - на рычажных весах и др.

Зависимость между измеряемой величиной X и результатом измерения Y при прямом измерении характеризуется уравнением X = Y, т.е. значение измеряемой величины принимается равным получен­ному результату.

К сожалению, прямое измерение не всегда можно провести. Иногда нет под рукой соответствующего измерительного прибора, или он неудовлетворяет.

по точности, или даже вообще ещё не создан. В этом случае приходится прибегать к косвенному измере­нию.

Косвенными измерениями называют та­кие измерения, при которых значение искомой величины находят на основании известной зависимости между этой величиной и величи­нами, подвергаемыми прямым измерениям. При косвенных измерениях измеряют не собственно определяемую величину, а другие величины, функционально с ней связанные. Значение измеряемой косвенным путем величины X находят вычислением по формуле

X = F(Y₁, Y₂, … ,Y_n),

где Y₁ , Y₂ , … Y_n - значения величин, полученных путем прямых измерений.

Примером косвенного измерения является определение электрического сопротивления с помощью амперметра и вольтметра. Здесь путем прямых измерений находят значения падения напряжения U на сопротивлении R и ток I через него, а искомое сопротивление R находят по формуле

R = U/I .

Операцию вычисления измеряемой величины может производить вручную или с помощью вычислительного устройства, помещенного в прибор.

Прямые и косвенные измерения в настоящее время широко использу­ются на практике и являются наиболее распространенными видами измерений .

Совокупные измерения - это производи­мые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.

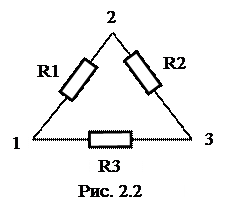Например, для определения значений сопротивлений резисторов, соединенных треугольником (рис. 2.2), измеряют сопротивления на каждой

паре вершин треугольника и получают систему уравнений

;

;

.

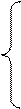
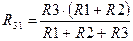Из решения этой системы уравнений получают значения сопротивлений

 

, , ,

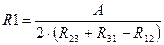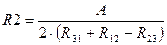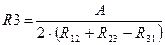где .

Совместные измерения - это производимые одновременно измерения двух или нескольких неодноименных величин X₁, X₂,…,X_n, значения которых находят решением системы уравнений:

F_i(X₁, X₂, … ,X_n; Y_i1, Y_i2, … ,Y_im) = 0,

где i = 1, 2, …, m > n; Y_i1, Y_i2, … ,Y_im - результаты прямых или косвенных измерений; X₁, X₂, … ,X_n – значения искомых величин.

Например, индуктивность катушки L = L₀×(1 + w²×C×L₀), где L₀ – индуктивность при частоте w = 2×p×f , стремящейся к нулю; С – межвитковая емкость. Значения L₀ и С нельзя найти прямыми или косвенными измерениями. Поэтому в простейшем случае измеряют L₁ при w₁ , а затем L₂ при w₂ и составляют систему уравнений:

L₁ = L₀×(1 + w₁²×C×L₀);

L₂ = L₀×(1 + w₂²×C×L₀),

решая которую, находят искомые значения индуктивности L₀ и емкости С:

; .

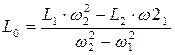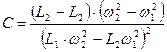Совокупные и совместные измерения есть обобщение косвен­ных измерений на случай нескольких величин.

Для повышения точности совокупных и совместных измерений обеспечивают условие m ³ n, т.е. число уравнений должно быть больше или равно числу искомых величин. Получающуюся при этом несовместную систему уравнений решают методом наименьших квадратов.

По числу наблюдений измерения подразделяются на (рис.2.1):

- обыкновенные измерения - измерения, выполняемые с однократным наблюдением;

- статистические измерения - измерения с многократными наблюдениями.

Наблюдение при измерении - экспериментальная операция, выполняемая в процессе измерений, в резуль­тате которой получают одно значение из группы значе­ний величин, подлежащих совместной обработке для по­лучения результатов измерений.

Результат наблюдения - результат величины, полу­чаемый при отдельном наблюдении.

По характеру зависимости измеряе­мой величины от времени измерения разделяются:

- на статические, при которых измеряемая величина оста­ется постоянной во времени в процессе измерения;

- дина­мические, при которых измеряемая величина изменяется в процессе измерения и является непостоянной во вре­мени.

При динамических измерениях для получения результата измерения необходимо учитывать это изменение. А для оценки точности результатов динамических измерений необходимо знание динамических свойств средств измерений [1].

По числу измеряемых мгновенных значений в заданном интервале времени измерения подразделяются на дискретные и непрерывные (аналоговые).

Дискретные измерения – измерения, при которых на заданном интервале времени число измеряемых мгновенных значений конечно.

Непрерывные (аналоговые) измерения – измерения, при которых на заданном интервале времени число измеряемых мгновенных значений бесконечно.

По условиям, определяющим точность результатов, измерения бывают:

- максимально воз­можной точности, достигаемой при существующем уров­не техники;

- контрольно-поверочные, погрешность кото­рых не должна превышать

некоторое заданное значение;

- технические, в которых погрешность результата опреде­ляется характеристиками средств измерений [11].

По способу выражения результатов измерения различают абсолютные и относительные измерения.

Абсолютные измерения – измерения, основанные на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.

Относительные измерения – измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную [12].

 

2.2. Методы измерений и их классификация

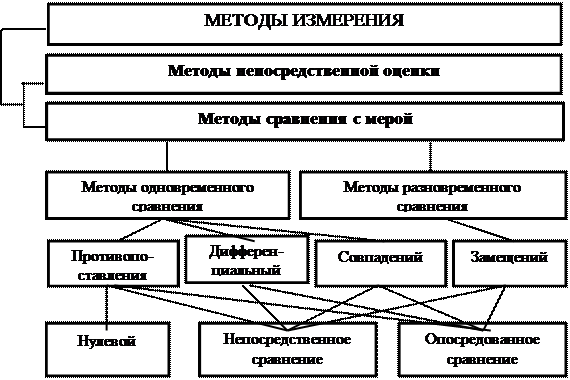
Все измерения могут производиться различными методами. Различают следующие основные методы измерений: метод непосредственной оценки и методы сравнения c мерой [7] .

2.2.1. Метод непосредственной оценки характеризуется тем, что значение измеряемой величины опреде­ляется непосредственно по отсчетному устройству измерительного прибора, заранее градуированного в единицах измеряемой величины. Этот метод является наиболее простым и поэтому широко применяется при измерении различных величин, например: измерение веса тела на пружинных весах, силы электрического тока стрелочным ампермет­ром, разности фаз цифровым фазометром и т.д.

Функциональная схема измерения методом непосредственной оценки приведена на рис. 2.3.

 

 

Приборы непосредственной оценки всегда содержат измерительный преобразователь, который преобразует измеряемую величину в другую, доступную для сравнения наблюдателем или автоматичес­ким устройством. Так, в стрелочных приборах происходит преобра­зование измеряемой величины в угол поворота подвижной части, ко­торый отмечается стрелкой. По положению стрелки, т.е. сравнени­ем угла поворота с делениями на шкале находится значение изме­ряемой величины. Мерой в приборах непосредственной оценки слу­жат деления шкалы отсчетного устройства. Они поставлены не произвольно, а на основании градуировки прибора. Градуировка прибора непосредственной оценки состоит в том, что на его вход от меры подается величина заданного размера и отмечается пока­зание прибора. Этому показанию затем присваивается значение известной величины. Таким образом, деления шкалы отсчетного устройс­тва являются как бы заменителем («отпечатком») значения реаль­ной физической величины и поэтому могут быть использованы не­посредственно для нахождения значений измеряемых прибором величин. Следовательно, все приборы непосредственной оценки факти­чески реализуют принцип сравнения с физическими величинами. Но это сравнение разновременное и осуществляется опосредованно, с помощью промежуточного средства – делений шкалы отсчетного устройства.

2.2.2. Методы сравнения с мерой – методы измерений, в которых известную величину сравнивают с величиной, воспроизводимой мерой. Эти методы по сравнению с методом непосредственной оценки более точны, но несколько сложны. Группа методов сравнения с мерой включает в себя следующие методы: противопоставления, нулевой, дифференциальный, совпадения и замещения.

Определяющим признаком методов сравнения является то, что в процессе каждого измерительного эксперимен­та происходит сравнение двух однородных независимых друг от друга величин - известной (воспроизводимой мерой) и измеряемой. При измерениях методами сравнения используются реальные физи­ческие меры, а не их «отпечатки».

Сравнение может быть одновременным, когда мера и измеряемая величина воздействуют на измерительный при­бор одновременно, и разновременным, когда воздей­ствие измеряемой величины и меры на измерительный прибор раз­несено во времени. Кроме того, сравнение может быть непосредственным и опосредован­ным. В первом случае измеряемая величина и мера непосредст­венно воздействуют на устройство сравнения, а во втором – через другие величины, однозначно связанные с известной и измеряемой величинами.

Одновременное сравнение осуществляется обычно методами противопоставления, нулевым, дифференциа­льным и совпадения, а разновременное - методом замещения.

Метод противопоставления – метод сравнения с мерой в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами [2]. Функциональная схема метода противоставления приведена на рис. 2.4.

В этом методе измеряемая величина Х и мера Х₀ воздействуют на два входа прибора сравнения. Результирующий эффект воздействия определяется разностью этих величин, т.е. e = Х - Х₀ и снимается с отсчетного устройства прибора сравнения. Результат измерения находят как

Y = X₀ + e .

Этот метод удобен, если имеются точная многозначная мера и несложные

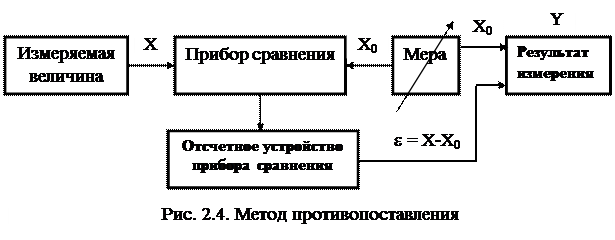устройства сравнения. Примером этого метода является взвешивание груза на равнопле­чих весах с помещением измеряемой массы и уравновешивающих её гирь на двух чашках весов и с полным уравновешиванием весов. При этом измеряемая масса определяется как сумма мас­сы гирь, её уравновешивающих, и показания по шкале весов. Метод противопоставления позволяет значительно уменьшить воздействие на результат измерений влияющих величин, поскольку последние более или менее одинаково искажают сигналы как в цепи преобразования измеряемой величины, так и в цепи преобразования величины, воспроизводимой мерой. Отсчетное устройство прибора сравнения реагирует на разность сигналов, вследствие чего эти искажения в некоторой степени компенсируют друг друга. Этот метод также применяют при измерении ЭДС, напряжения, тока и сопротивления [1].

Нулевой метод является разновидностью мето­да противопоставления, в котором результирующий эффект воз­действия величин на прибор сравнения доводят до нуля. Функциональная схема нулевого метода измерения приведена на рис. 2.5.

Здесь измеряемая величина X и мера X₀ воздействуют на два входа измерительного прибора сравнения. Результирующий эффект воздействия определяется разностью этих величин, т.е. e = X – X₀ . Изменяя величину, воспроизводимую мерой (это схематически указано на рисунке стрелкой), можно довести величину e до 0. Это обстоятельство отмечается индикатором нуля. Если e = 0, то Х = Хо, результат измерения Y есть полученное значение меры, т.е. Y = X₀ .

Поскольку на индикатор нуля воздействует разность вели­чин, то его предел измерения может быть выбран меньшим, а чувствительность большей, чем у прибора для измерения X методом непосредственной оценки. Точность индикации равенства двух величин может быть весьма большой. А это ведет к повышению точности измерения. Погрешность измерения нулевым методом определяется погрешностью меры и погрешностью индикации нуля. Вторая составляющая обычно много меньше первой, практически точность измерения нулевым методом равна точности меры.

Примерами нулевых методов измерений являются: измерение массы на равноплечих весах с помещением измеряемой массы и уравновешивающих её гирь на двух чашках весов и полным уравновешиванием весов или измерение напряжения путем компенсации его напряжением образцового источника (в обоих случаях осуществляется непосредственное сравнение); а также измерение электрического сопротивления мостом с полным его уравновешиванием (опосредованное сравнение).

Нулевой метод измерения требует обязательного применения многозначных мер. Точность таких мер всегда хуже однозначных мер, кроме того, мы можем не иметь меры переменной величины. В таком случае нулевой метод не применим.

Дифференциальный метод представляет собой метод сравнения с мерой, в котором на измерительный прибор (обязательно прибор сравнения) воздействует разность измеряемой величины и известной величины, воспроизводимой мерой, причем эта разность не доводится до нуля, а измеряется измерительным прибором прямого действия.

На рис. 2.6 показана функциональная схема дифференциального метода.

Здесь мера имеет постоянное значение Х₀, разность измеряемой величины Х и меры Х₀, т.е. e = Х - Х₀, не равна ну­лю и измеряется измерительным прибором. Результат измерения на­ходятся как

Y = X₀ + e .

То обстоятельство, что здесь измерительный прибор измеряет не всю величину Х, а только её часть e, позволяет уменьшить влияние на результат измерения погрешности измерительного прибора, причем влияние погрешности измерительного прибора тем меньше, чем меньше разность e .

Действительно, при измерении напряжения U = 97 В вольтметром непосредственной оценки с пределом измерения 100 В и допущенной относительной погрешности измерения этого напряжения 1 % (0,01) мы получаем абсолютную погрешность измерения D₁ = 97×0,01 = 0,97 » 1 В. Если же будем измерять это напряжение дифференциальным методом с использованием образцового источника напряжения U₀ = 100 В, то разность напряжений U – U₀ = (97 - 100)В = - 3 В мы можем измерить вольтметром с пределом измерения всего 3 В. Пусть относительная погрешность измерения этого напряжения будет также равна 1 % . Это даёт абсолютную погрешность измерения напряжения 3 В: D₂ = 3×0,01 = 0,03 В . Если эту погрешность привести к измеряемому напряжению U , мы получим относительную погрешность измерения напряжения: D₂/U = 0,03/97 » 0,0003 (0,03 %), т.е. приблизительно в 30 раз меньше, чем при измерении напряжения U методом непосредственной оценки. Это увеличение точности измерения произошло потому, что в первом случае прибором была измерена почти вся величина с относительной погрешностью в 1 % , а во втором случае измеряется не вся величина, а только её 1/30 часть.

В этих расчетах не учитывалась погрешность меры, кото­рая полностью входит в результат измерения. Следовательно, при малых разностных величинах e точность измерения дифферен­циальным методом приближается к точности измерения нулевым ме­тодом и определяется лишь погрешностью меры. Кроме того, диф­ференциальный метод не требует меры переменной величины.

В приведенном выше примере измерения напряжения дифферен­циальным методом использовалось непосредственное сравнение.

Другим примером дифференциального метода измерения может служить определение отклонения сопротивления резистора от но­минала неуравновешенным (процентным) мостом (здесь реализуется опосредованное сравнение).

Метод совпадений (или метод «нониуса») представляет собой метод сравнения с мерой, в котором разность между измеряемой величи­ной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов.

Этот метод применяется в тех случаях, когда измеряемая величина меньше цены деления заданной меры. При этом применяются две меры с разными ценами деления, которые отлича­ются на размер оцениваемого разряда отсчетов.

Пусть имеем одну калиброванную меру с ценой деления Dx_k1 и изме­ряемую величину Dx, которая меньше цены деления. В этом случае исполь­зуют вторую меру с ценой деления Dx_k2 . Таким образом, если чувствитель­ность необходимо увеличить в п раз, то соотношение между ними будет иметь вид

Dx_k2 = Dx_k1×(1 - 1/n).

В частности, при n = 10 Dx_k2 =0,9 ×Dx_k1 .

Измеряемую величину Dx устанавливают между нулевыми отметками мер и находят число N_x, равное номеру совпавших делений мер (рис. 2.7). В этом случае справедливо соотношение N_x×Dx_k1 = Dx + N_x×Dx_k2 ,откуда

Dx = N_x×( Dx_k1 - Dx_k2) = N_x×(Dx_k1 – 0,9×Dx_k1) = N_x×0,1×Dx_k1 .

Примером измерения методом совпадения может служить измерение длины детали с помощью штангенциркуля с нониусом, другим примером - измерение частоты вращения детали с помощью мигающей лампы стробоскопа: наблюдая положение метки на вращающейся детали в моменты вспышек лампы, по частоте вспышек и смещению метки определяют частоту вращения детали. Метод "нониуса" находит также широкое применение при измерении времен­ных интервалов двух близких частот (биений) и в других случаях [5].

Функциональная схема прибора, работающего по методу совпадений с масштабным преобразованием только величины, воспроизводимой ме­рой, показана на рис. 2.8. Здесь величина X₀ однозначной меры подвергается масштабному преобразованию для выработки величин n₁X₀, n₂X₀, … n_jX₀, … n_kX₀, Эти величина подаются на k- устройств сравнения, к ним же прикладывается и измеряемая величина Х. Логическое устройство указывает номер устройства сравнения, у которого Х - n_jX₀ = min и определяет измеряемую величину на основе приближенного соотношения X = n_jX₀. Такой метод измерения нашел применение также в цифровых приборах, измеряющих угловые и линейные перемещения. Метод совпадения требует наличия многозначных мер или масштабных преобразователей величины и величины, воспроизводимой мерой. Поэтому в измерительной технике он используется сравнительно редко.

Метод замещения есть метод сравнения с ме­рой, в котором измеряемую величину замещают известной величи­ной, воспроизводимой мерой [2].

Функциональная схема метода замещения изображена на рис. 2.9. В нем используется измерительный прибор непосредственной оцен­ки.

Техника измерения состоит в следующем. Сначала на вход из­мерительного прибора подают измеряемую величину Х и отмечают показания прибора (отсчет) Y₁ . После этого вместо измеряемой величины на тот же самый

 

 

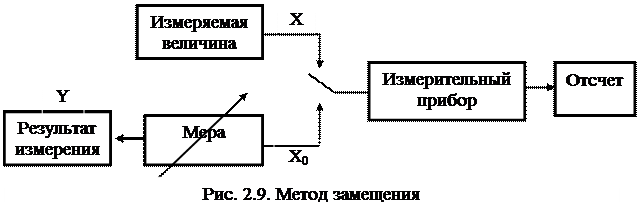вход (это очень существенно) прибора подают величину Х₀, воспроизводимую мерой. В этом случае показание прибора становится равным Y₂. Изменяя величину, воспроизводимую мерой, добиваются равенства показаний, т.е. Y₁= Y₂ . При этом можно утверждать, что Х = Х₀ независимо от погрешности измерительного прибора. Действительно, в первом случае получаем Y₁= X + D₁,

где D₁ - погрешность измерительного прибора при получении отсчета Y₁ .

При воздействии на прибор меры Y₂= X + D₂. Здесь D₂ - погрешность измерительного прибора при получении отсчета Y_2.

Поскольку мы добиваемся одинаковых показаний ( Y₁ = Y₂ ), а интервал времени между двумя измерениями невелик, то на одной и той же отметке шкалы прибора погрешность одинакова, т.е. D₁ = D₂ . Следовательно, из равенства Y₁ = Y₂ или X + D₁ = X + D₂ вытекает, что Х = Х_0.

Исключение погрешности измерительного прибора из результата измерений является новым достоинством метода замещения. В нулевом методе измерения погрешность измерительного прибора проявляет себя тем, что нулевое показание может не соответствовать равенству измеряемой величины и меры, а в дифференциальном методе она представляет собой погрешность измерения разности меры и измеряемой величины. Для получения большой точности измерения нулевым и дифференциальным методом необходимо, чтобы погрешности измерительных приборов были невелики. А вот метод замещения не требует этого условия! Даже если погрешность измерительного прибора достаточно велика, это не скажется на результате измерения. Таким образом, методом замещения можно осуществить точное измерение, имея прибор с большой погрешностью. Нетрудно сообразить, что точность измерения методом замещения определяется погрешностью меры. Правда, при более строгом подходе к методу замещения следует учитывать два обстоятельства.

Во-первых, здесь сравнение разновременное, а за время между двумя измерениями погрешность измерительного прибора может несколько измениться, так что равенство D₁ = D₂ несколько нарушится. Теперь становится ясно, почему измеряемая величина и мера должны подаваться на один и тот же вход прибора. Это прежде всего связано с тем, что погрешность измерительного прибора на разных входах даже при одинаковых показаниях может быть разной!

Во-вторых, метод замещения сводится к получению одинаковых показаний прибора. Само равенство показаний может быть ус­тановлено с конечной точностью. А это также ведет к погрешности измерения. Точность установления равенства показаний будет больше в приборе, обладающем большей чувствительностью.

Следовательно, при измерении методом замещения следует использовать не точный, но чувствительный и быстродействующий прибор. Тогда остаточ-ная погрешность, обусловленная измерительным прибором, будет невелика.

Метод замещения является самым точным из всех известных методов и обычно используется для проведения наиболее точных (прецизионных) измерений. Ярким примером метода замещения является взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов (вспомните - на один и тот же вход прибора). Известно, что таким методом можно правильно измерить массу тела, имея неверные весы (погрешность прибора), но никак не гири! (погрешность меры).

Сравнивая между собой метод замещения и метод непосредственной оценки, мы обнаружим их разительное сходство. Действительно, метод непосредственной оценки по своей сути представляет метод замещения. Почему он выделен в отдельный метод? Все дело в том, что при измерении методом непосредственной оценки мы выполняем только первую операцию - определение показаний. Вторая операция - градуировка (сравнение с мерой) производится не при каждом измерении, а лишь в процессе производства прибора и его периодических поверках. Между применением прибора и его предыдущей поверкой может лежать большой интервал времени, а погрешность измерительного прибора за это время может значительно измениться. Это и при­водит к тому, что метод непосредственной оценки дает обычно меньшую точность измерения, чем метод сравнения [7].

Рассмотренная классификация методов измерений изображена на рис. 2.10.

		Рис. 2.10. Классификация методов измерений

 

Рассмотренные методы определяют принципы постро­ения измерительных приборов. Их не следует путать с методикой измерения и алгоритмом измерения.

Методика измерений - детально намеченный поря­док процесса измерений, регламентирующий методы, средства, алгоритмы выполнения измерений, которые в определенных (нормированных) условиях обеспечива­ют измерения с заданной точностью.

Измерения должны осуществляться в соответствии с аттестованными в установленном порядке методиками. Порядок разработки и аттестации методик выполнения измерений определяется Госстандартом России.

Алгоритм измерения - точное предписание о выпол­нении в определенном порядке совокупности операций, обеспечивающих измерение значения физической вели­чины.

 

СРЕДСТВА ИЗМЕРЕНИЙ

Классификация средств измерений

Средства измерений - технические средства, ис­пользуемые при измерениях и имеющие нормированные метрологические свойства.

По назначению средства измерений разделяют на меры, измерительные преобра­зователи, измерительные приборы, измерительные уста­новки и измерительные системы (рис. 3.1) [1]. По метрологическому назначению средства измерений делят на образцовые и рабочие [4].

Образцовые средства измерений предназначены для поверки по ним как рабочих, так и образцовых средств измерений менее высокой точности. Процесс передачи размера единиц от образцовых средств измерений высшей точности рабочим и образ­цовым средствам измерений более низкой точности

 

 

представляет собой поверку средств измерений, поэтому все образцовые средст­ва измерения являются средствами поверки.

Рабочие средства измерений применяются для измерений, не связанных с передачей размера единиц. Они предназначены для измерений раз­меров величин, необходимых в разнообразной деятельности чело­века.

Каждое средство измерения должно применяться только по своему прямому назначению. Не разрешается применять рабочие средства измерений для проведения поверочных работ; точно так же запрещается использование образцовых средств для измерений, не связанных с поверкой.

Запрещение применять образцовые средства измерений для практических измерений - одно из важнейших требований метро­логии. Однако им нередко пренебрегают или недооценивают его значение. Каким бы точным не было бы средство измерений, применяемое для практических измерений, его нельзя использовать для поверки других средств измерений. Само оно должно пове­ряться по образцовому средству измерений, имеющему более вы­сокую точность [4].

 

Меры и наборы мер

Существуют однозначные и многозначные (переменные) меры (рис. 3.2). Мера, воспроизводящая физическую величину одного размера, называется…      

Измерительные преобразователи

Измерительные преобразователи являются составными частями измерительных приборов, установок и систем. Измерительные преобразователи можно… Физические величины могут быть непрерывными по значению и квантованными (они…    

Измерительные приборы

Выработка измерительной информации может основываться на использовании различных физических принципов. Например, для из­мерения длины применяют… Физический принцип, положенный в основу построения изме­рительного прибора,… Принципиально измерительный прибор состоит из ряда изме­рительных преобразователей, каналов связи, согласующих…

Измерительные установки и системы

Измерительные установки в большинстве случаев обладают большей или меньшей универсальностью как в отношении номен­клатуры измеряемых величин, так и… Измерительная система также представляет собой совокупность средств измерений… Средства измерений могут находиться в разных местах, а пере­дача измерительной информации осуществляться по…

Метрологические характеристики средств измерений

Метрологическими характеристиками средств измерений называются такие характеристики их свойств, которые оказывают влияние на результаты и… Измеряемая, преобразуемая или воспроизводимая (для мер) величина. Этот… Предел и диапазон измерений. Очень важной характеристикой любого средства измерения, определяющей в первую очередь…

Погрешности средств измерений

Согласно ГОСТ 8.009—84, следует различать четыре составляющие погрешности средств измерений: основ­ную; дополнительную; обусловленную… Основная погрешность. Она обусловлена неидеаль­ностью собственных свойств… По способу числового выражения основной погреш­ности различают абсолютную, относительную и приве­денную погрешности. …

Нормирование метрологических характеристик средств измерений

Эти сведения приводят в нормативно-технической докумен­тации на средства измерений, а наиболее важные из них ука­зывают на самих средствах. Установление номинальных значений и границ допускаемых отклонений реальных… Общим вопросам нормирования метрологических характери­стик средств измерений посвящен ГОСТ 8.009—84 «Нормирова­ние и…

Способы выражения пределов допускаемых погрешностей средств измерений

Пределом допускаемой погрешности (допускаемой погрешностью) средств измерений называется наибольшая (без учета знака) его погрешность, при которой… Вопросы нормирования погрешностей средств измерений рассмотрены в ГОСТ… Согласно этому стандарту, пределы допускаемых основной и дополнительных погрешностей выражают в форме приведен­ных,…

Классы точности средств измерений

Рассмотренные метрологические характеристики позволяют выявить такую качественную характеристику как точность средств измерений, положенную в основу деления средств измерений на классы точности.

Класс точности средства измерений - это его обобщенная характеристика, определяемая пределами допускае­мых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений.

Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показате­лем точности измерений, выполняемых с помощью этих средств.

Общие положения о делении средств измерений на классы точ­ности и способы нормирования метрологических характеристик регламентированы ГОСТ 8.401—80. Однако этот стандарт не уста­навливает классы точности средств измерения, для которых преду­смотрены нормы отдельно для систематической и случайной состав­ляющих погрешности, а также если необходимо учитывать дина­мические характеристики.

Если класс точности прибора установлен по пределу допускаемой относительной основной погрешности, т.е по значению погрешности чувствительности [см. формулу (3.20)] и форма полосы погрешности принята чисто мультипликативной, обозначаемое на шкале значение класса точности обводится кружком. Например, обозначает, что d_доп = 1,5 %.

Если же полоса погрешности принята аддитивной и прибор нормируется по пределу допускаемой приведенной основной погрешности [см. формулу (3.19)], т.е. по значению погрешности нуля (таких приборов большинство), то класс точности указывается на шкале без каких-либо подчеркиваний. Например, 1,5 обозначает, что g_доп=1,5 %.

Если шкала прибора неравномерная (например, у омметров), предел допускаемой основной приведенной погрешности выражается формулой (3.19), а нормирующее значение принято равным длине шкалы или ее части, класс точности обозначается на шкале одним числом, помещенным между двумя линиями, расположенными под углом. Например, 1,5 , это означает, что g_доп=1,5 %.

Если средство измерений обладает как аддитивной, так и мультипликативной полосой погрешности, а пределы допускаемой относительной погрешности в процентах устанавливаются формулой (3.21), например,

,

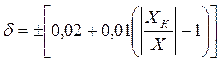где с = 0,02; d = 0,01, то обозначение в документации будет «класс точности

0,02/0,01», а на приборе 0,02/0,01. Таким образом, для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме относительных погрешностей [см. формулу (3.21) ], классы точности обозначают числами с и d (в процентах), разделяя их косой чертой.

Для средств измерений, пределы допускаемой основной погреш­ности которых принято выражать в форме абсолютных погрешнос­тей по формулам (3.17) или (3.18) или относительных в виде графи­ка, таблицы или формулы, отличной от формул (3.20) и (3.21), клас­сы точности обозначают прописными буквами латинского алфавита или римскими цифрами. Классы точности, которым соответствуют меньшие пределы допускаемых погрешностей, должны обозначать­ся буквами, находящимися ближе к началу алфавита, или цифра­ми, означающими меньшие числа.

Для всех рассмотренных случаев вместе с условным обозначе­нием класса точности на шкале, щитке или корпусе средств измерений наносится номер стандарта или технических условий, устанавливающих технические требования на эти средства изме­рений.

Классы точности цифровых измерительных приборов со встроенными вычислительными устройствами для дополнитель­ной обработки результатов измерений устанавливают без режи­ма обработки.

При указании классов точности на измерительных приборах с существенно неравномерной шкалой допускается указывать пределы допускаемой основной относительной погрешности для части шкалы, лежащей в пределах, отмеченных специальными знаками, например точками или треугольниками.

Таким образом, обозначение класса точности средства измерений дает достаточно полную информацию для вычисления приближенной оценки погрешностей результатов измерений.

 

 

Погрешности измерений

выполнения измерений результаты измерений отличаются от истинного значе­ния измеряемой величины, т.е. неизбежны погрешности измерений. При оценке… Погрешность — это отклонение результата измерения от ис­тинного значения… Погрешности средств измерения были рассмотрены в главе 3.

Абсолютные и относительные погрешности

Поскольку истинное значение измеряемой величины определить невозможно, вместо него на практике используют действитель­ное значение измеряемой… 4.2. Погрешности инструментальные и мето­дические,

Отсчитывания и установки

Эти погрешности обусловлены конструктивными и технологическими недостатками средств измерений, а также следствием их износа, старения или… Однако, кроме инструментальных погрешностей, при измерениях возникают еще и… Методические погрешности могут возникать из-за не­совершенства разработки теории явлений, положенных в основу метода…

Систематические, прогрессирующие, случайные и грубые погрешности

Причины воз­никновения систематических погрешностей обычно могут быть установ­лены при подготовке и проведении измерений. Эти причины весьма… Результат измерений тем ближе к истинному значению измеряемой величины, чем… Прогрессирующими (или дрейфовыми) называются непредсказуе­мые погрешности, медленно изменяющиеся во времени. Эти…

Вероятностный подход к описанию погрешностей

Пусть величину А измеряли п раз и наблюдали при этом значе­ния а1, a2, а3,…,аi,...,аn. Случайная абсолютная погрешность еди­ничного измерения… Di = ai – A . (4.1) Графически результаты от­дельных измерений представ­лены на рис. 4.2.

Таблица 4.1

n	Значения квантилей распределения Стьюдента t(n) при доверительной вероятности Рд
0,5	0,6	0,7	0,8	0,9	0,95	0,98	0.99	0,995	0,999
	1.000	1.376	1,963	3,080	6,310	12,71	31,80	63,70	127,3	637,2
	0.816	1,061	1,336	1,886	2,920	4,30	6,96	9,92	14,10	31,60
	0.765	0.978	1,250	1,638	2,350	3,18	4,54	5,84	7,50	12,94
	0.741	0.941	1,190	1,533	2,130	2,77	3,75	4,60	5,60	8,61
	0,727	0.920	1,156	1,476	2,020	2,57	3,36	4,03	4,77	6,86
	0,718	0.906	1,134	1,440	1,943	2,45	3,14	3,71	4,32	5,96
	0.711	0.896	1,119	1,415	1,895	2,36	3,00	3,50	4,03	5,40
	0.706	0.889	1,108	1,397	1,860	2,31	2,90	3,36	3,83	5,04
	0,703	0.883	1,110	1,383	1,833	2,26	2,82	3,25	3,69	4,78
	0.700	0.879	1,093	1,372	1,812	2,23	2,76	3,17	3,58	4,59
	0.697	0.876	1,088	1.363	1,796	2,20	2,72	3,11	3,50	4,49
	0.695	0.873	1,083	1,356	1,782	2,18	2,68	3,06	3,43	4,32
	0.694	0.870	1,079	1,350	1,771	2,16	2,65	3,01	3,37	4,22
	0.692	0,868	1,076	1,345	1,761	2,14	2,62	2,98	3,33	4,14
	0.691	0,866	1,074	1,341	1,753	2,13	2,60	2,95	3,29	4,07
	0.690	0.865	1,071	1,337	1,746	2,12	2,58	2,02	3,25	4,02
	0,689	0.863	1,069	1,333	1,740	2,11	2,57	2,90	3,22	3,96
	0.688	0,862	1,067	1,330	1,734	2,10	2,55	2,88	3,20	3,92
	0.688	0.861	1,066	1,328	1,729	2,09	2,54	2,86	3,17	3,88
¥	0,674	0,842	1,036	1,282	1,645	1,96	2,33	2,58	2,81	3,29

 

Оценка погрешностей результатов косвенных измерений. При косвенных измерениях искомая величина А функционально связана с одной или несколькими непосредственно измеряемыми ве­личинами: х, y,...,t. Рассмотрим простейший случай определения по­грешности при одной переменной, когда A=F(x). Обозначив абсо­лютную погрешность измерения величины х через ±Dx , получим A+DA = F(x±Dx).

Разложив правую часть этого равенства в ряд Тейлора и прене­брегая членами разложения, содержащими Dх в степени выше пер­вой, получим

A+DA » F(x) ± 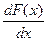Dx или DA » ± 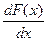Dx.

Относительная ошибка измерения функции определится из выраже­ния

.

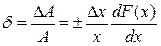Если измеряемая величина А является функцией нескольких пе­ременных: A=F(x, y,...,t), то абсолютная погрешность результата косвенных измерений

.

Частные относительные погрешности косвенного измерения опреде­ляются по формулам ; 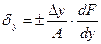и т. д. Относительная погрешность результата измерений

.

Остановимся также на особенностях оценки результата косвенного измерения при наличии случайной погрешности.

Для оценки случайной погрешности результатов косвенных измерений величины А бу­дем полагать, что систематические погрешности измерений вели­чин x, y,…, t исключены, а случайные погрешности измерения этих же величин не зависят друг от друга.

При косвенных измерениях значение измеряемой величины на­ходят по формуле ,

где 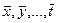- средние или средние взвешенные значения величин x, y,…, t .

Для вычисления среднего квадратического отклонения значе­ния 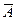измеряемой величины А целесообразно использовать сред­ние квадратические отклонения, полученные при измерениях x, y,…, t .

В общем виде для определения среднего квадратического от­клонения s косвенного измерения служит следующая формула:

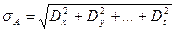, (4.7)

где D_x ; D_y ;…; D_t — так называемые частные погрешности косвенного измерения 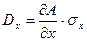; ; …; ; ; ; … ; 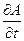— частные производные А по x, y,…, t ; s_x; s_y ,…, s_t , …— средние квадратические отклонения результатов измере­ний величин x, y,…, t .

Рассмотрим некоторые частные случаи применения уравнения (4.7), когда функциональная зависимость между косвенно и непосредственно измеряемыми величинами выражается формулой A = k×x^a×y^b×z^g , где k - числовой коэффициент (безразмерный).

В этом случае формула (4.7) примет следующий вид:

.

Если a = b = g = 1 и A = k×x×y×z, то формула относительной по­грешности упрощается до вида .

Эта формула применима, например, для вычисления среднего квадратического отклонения результата измерения объема по ре­зультатам измерения высоты, ширины и глубины резервуара, име­ющего форму прямоугольного параллелепипеда.

 

4.5. Правила суммирования случайных и систематических погрешностей

Погрешность сложных измерительных приборов зависит от по­грешностей отдельных его узлов (блоков). Погрешности суммиру­ются по определенным правилам.

Пусть, например, измерительный прибор состоит из m блоков, каждый из которых обладает независимыми друг от друга случай­ными погрешностями. При этом известны абсолютные значения средних квадратических s_k или максимальных М_k погрешностей каждого блока.

Арифметическое суммирование или дает максимальную погрешность прибора, которая имеет ничтожно малую вероятность и поэтому редко используется для оценки точности ра­боты прибора в целом. Согласно теории ошибок результирующая погрешность s_рез и М_рез определяется сложением по квадратическому закону 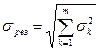или .

Аналогично определяется и результирующая относительная по­грешность измерения: . (4.8)

Уравнение (4.8) можно использовать для определения допу­стимых погрешностей отдельных блоков разрабатываемых прибо­ров с заданной общей погрешностью измерения. При конструирова­нии прибора обычно задаются равными погрешностями для отдель­ных входящих в него блоков. Если существует несколько источни­ков погрешностей, которые на конечный результат измерения влияют неодинаково (или прибор состоит из нескольких блоков с разными погрешностями), в формулу (4.8) следует ввести весовые коэффициенты k_i :

, (4.9)

где d₁, d₂, … , d_m — относительные погрешности отдельных узлов (бло­ков) измерительного прибора; k₁, k₂, … , k_m - коэффициенты, учиты­вающие степень влияния случайной погрешности данного блока на результат измерения.

При наличии у измерительного прибора (или его блоков) также и систематических погрешностей общая погрешность определяется их суммой:

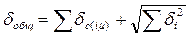, где d_с(im) - система­тическая погрешность от воздейст- вия на i-й блок m-го фактора; d_i - случайные погрешности для i-го блока.

Суммирование погрешностей, имеющих взаимную корреляцион­ную связь, основано на следующем положении теории вероятностей: дисперсия суммы двух коррелированных случайных величин, харак­теризующихся дисперсиями и и коэффициентом корреля­ции r₁₂, определяется выражением

.

Из этого следует, что средняя квадратическая результирующая по­грешность вычисляется по формуле

. (4.10)

На практике обычно пользуются двумя крайними случаями формулы (4.10); при r₁₂ » ±1, когда составляющие погрешности суммируют­ся алгебраически: = s₁+ s₂ и при r₁₂ » 0 , когда погрешности суммируются геометрически: . Такой же подход справедлив и для большего числа составляю­щих.

При оценке влияния частных погрешностей следует учитывать, что точность измерений в основном зависит от погрешностей, боль­ших по абсолютной величине, а некоторые наименьшие погрешно­сти можно вообще не учитывать. Частная погрешность оценивается на основании так называемого критерия ничтожной погрешности, который заключается в следующем. Допустим, что суммарная по­грешность d_рез определена по формуле (4.8) с учетом всех m частных погрешностей, среди которых некоторая погрешность d_i имеет ма­лое значение. Если суммарная погрешность d^¢_рез, вычисленная без учета погрешности d_i, отличается от d_рез не более чем на 5 %, т.е. d_рез-d^¢_рез< 0,05×d_рез или 0,95×d_рез<d^¢_рез , то d_i можно считать ничтожной погрешностью. Принимая во внимание, что (d^¢_рез)² = d²_рез - d²_i , легко установить критерий ничтожной погрешности: d_i £ 0,3×d_рез . Это означает, что если частная погрешность меньше 30 % общей погрешности, то этой частной погрешностью можно пренебречь. В случае нескольких погрешностей критерий ничтожности их сово­купности имеет вид .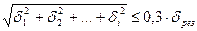

В практике технических расчетов часто пользуются менее стро­гим критерием - в эти формулы вводят коэффициент 0,4.

 

Формы представления результатов измерения

Погрешность результата прямого однократного измерения зависит от многих факторов, но в первую очередь определяется погрешностью используемых средств… погрешности, которой в данной точке диапазона измерений харак­теризуется… Погрешности средств измерений изменяются в диапазоне измерений. Поэтому в каждом случае, для каждого измерения…

ЭТАЛОНЫ. ОБРАЗЦОВЫЕ И РАБОЧИЕ МЕРЫ

Единство измерений достигается путем точного воспроизведе­ния и хранения установленных единиц физических величин и пе­редачи их размеров применяемым… Размеры единиц воспроизводятся, хранятся и передаются с по­мощью эталонов и… Высшим звеном в метрологической цепи передачи размеров единиц измерений являются эталоны.

Эталоны

Эталоны делят на первичные, специальные и вторичные. Первичный эталон обеспечивает воспроизведение единицы с наивысшей в стране точностью (по сравнению с другими этало­нами той же единицы). Первичный эталон основной единицы дол­жен…

Меры электрических величин

По точности воспроизведения физической величины образцо­вые меры бывают 1, 2 и 3-го разрядов, причем наименьшая по­грешность воспроизведения у меры… По наименованию воспроизводимой единицы меры делятся на меры э.д.с. или… Меры э.д.с. и электрического напряжения. В качестве образцовой меры э.д.с. используют нормальные элементы (НЭ). НЭ…

ОРГАНИЗАЦИОННЫЕ ОСНОВЫ МЕТРОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ

 

Об обеспечении единства измерений

В интересах общества необходимо, чтобы измерения, где бы они не выполнялись, обеспечивали получение согласуемых между собой результатов, т.е. чтобы… Единство измерений - характеристика качества измерений, заключающаяся в том,… Единство измерений, определенное в ГОСТ 16263-70 как состояние измерений, при котором их результаты выражены в…

Государственное управление обеспечением единства измерений

К компетенции Госстандарта России отно­сятся: - межрегиональная и межотраслевая координа­ция деятельности по обеспечению… - представление Правительству Российской Федерации предложений по единицам величин, до­пускаемым к применению;

Государственный метрологический контроль и надзор

- утверждение типа средств измерений; - поверку средств измерений, в том числе эталонов; - лицензирование деятельности юридических и физических лиц по изго-товлению, ремонту, продаже и прокату средств…

Калибровка и сертификация средств измерений

Средства измерений, не подлежащие поверке, могут подвергаться калибровке, при выпуске из производства или ремонта, при ввозе по импорту, при… Калибровка средств измерений производится метрологическими службами… Результаты калибровки средств измерений удостоверяются калибровочным знаком, наносимым на средства измерений, или…

Б И Б Л И О Г Р А Ф И Я

2. ГОСТ 16263-70 ГСИ. Метрология. Термины и определения. –М.: Изд-во стандартов, 1985. – 54 с. 3. Основные термины в области метрологии: Словарь-справочник /М.Ф. Юдин и др.;… 4. Тюрин Н.И. Введение в метрологию: Учеб. пособие. – М.: Изд-во стандартов, 1985. -248 с.

ОГЛАВЛЕНИЕ

Введение ………………………………………………………………...…. 3

1. Метрология. Основные понятия в области измерений ……………….. 4

1.1. Основные понятия и определения ………………………………….. 5

1.2. Измерение. Измеряемые величины ………………………………… 5

1.3. Физическая величина. Единицы физической величины …………. 10

1.4. Системы единиц физических величин ….………………………….11

1.5. Размер величины. Значение величины ……………………………14

1.6. Размерность физических величин …………………………………15

1.7. Измерительное преобразование …………………………………...16

1.8. Вид измерений ………………………………………………………16

1.9. Методы и средства измерений ……………………………………..16

1.10. Меры …………………………………………………………………17

1.11. Эталоны единиц физических величин. Образцовые

средства измерений ………………………………………………...17

1.12. Точность измерений ………………………………………………...18

1.13. Погрешность измерений ……………………………………………19

1.14. Поверка средств измерений ………………………………………...19

2. Виды и методы измерений ……………………………………………….21

2.1. Классификация видов измерений …………………………………..21

2.2. Методы измерений и их классификация …………………………...25

2.2.1. Методы непосредственной оценки ………………………………..25

2.2.2. Методы сравнения с мерой ………………………………………..26

3. Средства измерений ………………………………………………………34

3.1. Классификация средств измерений….……………………………...34

3.2. Меры и наборы мер ………………………………………………….35

3.3. Измерительные преобразователи ……………………………..……36

3.4. Измерительные приборы ……………………………………………40

3.5. Измерительные установки и системы ………….…………………..48

3.6. Метрологические характеристики средств измерений …………...49

3.7. Погрешности средств измерений …………………………………..58

3.8. Нормирование метрологических характеристик

средств измерений……………………………………………………64

3.9. Способы выражения пределов допускаемых

Погрешностей средств измерений ………………………………….65

3.10. Классы точности средств измерений ……………………………….68

4.

Погрешности измерений ………………………………………………..70

4.1. Абсолютные и относительные погрешности …………………….70

4.2. Погрешности инструментальные и методические,

Отсчитывания и установки ………………………………………..71

4.3. Систематические, прогрессирующие, случайные

и грубые погрешности …………………………………………….73

4.4. Вероятностный подход к описанию погрешностей ……………..75

4.5. Правила суммирования случайных и систематических

погрешностей ……………………………………………………....84

4.6. Формы представления результатов измерений ………………….86

5. Эталоны. Образцовые и рабочие меры………………………………....88

5.1. Эталоны…..………………………………………………………….88

5.2. Меры электрических величин ……………………………………..92

6. Организационные основы метрологического обеспечения …………..99

6.1. Об обеспечении единства измерений ……………………………..99

6.2. Государственное управление обеспечением единства

измерений …………………………………………………………101

6.3. Нормативные документы по обеспечению единства

измерений ………………………………………………………….102

6.4. Метрологические службы России ………………………………..102

6.5. Государственный метрологический контроль и надзор ………..104

6.6. Калибровка и сертификация средств измерений………………...107

 

 

* Закон №3, 1994, С. 29-35