На основе многократного измерения
Многократное (n-кратное) измерение одной и той же величины Х, дающее ряд однократных измерений 
, позволяет:
Во-первых, повысить точность конкретного результата измерения - за счёт усреднения значений , при котором, очевидно, будет существенно уменьшена случайная погрешность (СП);
Во-вторых, обработка результатов многократного измерения позволяет оценить СКО s случайной погрешности e, её закон распределения, а также граничные значения ± eг.= ±tP s её доверительного интервала при последующих измерениях теми же средствами.
Следует помнить,что поскольку на практике, число единичных измерений , входящих в n-кратное измерение, всегда ограничено, найти можно лишь оценочные (приближённые) значения характеристик случайных погрешностей, которые называются оценками этих характеристик. Качественным отличием оценок от самих характеристик, которые являются детерминированными числами (или зависимостями), является то, что оценки характеристик содержат случайную составляющую, изменяющуюся при изменении числа n n-кратного измерения..
. Известно, что оценки, получаемые по статистическим данным, имеют наибольшую достоверность, если они удовлетворяют требованиям состоятельности, несмещённости и эффективности.
Оценка Q' некой числовой характеристики Q случайной величины считается:
- состоятельной, если при n→∞ оценка Q'→ Q;
- несмещенной, если математическое ожидание этой оценки M[Q']= Q;
- эффективной, если дисперсия оценки минимальна, т.е. D[Q']=min.
Будем считать, что многократные измерения проводятся одним прибором или одинаковыми по точности приборами, в одинаковых условиях и с одинаковой тщательностью. При этом получаем ряд равноточных измерений
(15)
каждое из которых содержит систематическую 
и случайную ε погрешность, т.е. 
*) (15а)
Статистическая обработка результатов многократного измерения предполагает следующие действия:
1.Прежде всего, нужно постараться, если возможно, выявить и исключить систематическую погрешность, которую может содержать ряд (15), т.е. найти 
. В результате получим исправленныйряд измерений
X1, X2, …Xn (16)
Отметим, что такое исправление ряда позволит существенно повысить точность результата многократного измерения, но не повлияет на оценку характеристик случайной погрешности.
2.Определение результата n-кратного измерения.Очевидно, что этим результатом является среднее арифметическое значение ряда (16):
(17)
Если предварительное исключение из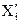 
удалось выполнить до пренебрежимо малого остаточного уровня, то, очевидно, 
,
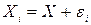а 
, где 
(18)
есть случайная погрешность результата n-кратного измерения.
Заметим: если известно, что систематическая погрешность постоянна, то её можно исключать из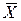 
, а не из каждого Xi по отдельности (как это рекомендовалось в п.1).
Если не исключалась, то результат многократного измерения 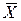, найденный путём усреднения одиночных измерений 
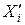можно записать в виде
, (18)
Поскольку при n→∞, 
→M[εi]=0, ясно, что многократное измерение позволяет значительно уменьшить случайную составляющую погрешности, и без изменения систематической .
3.Оценка СКО единичных и многократных измерений. Очевидно, что найденное по формуле (18) 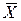есть оценка 
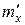математического ожидания
mx=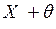
. Поэтому можно оценить случайную погрешность каждого единичного измерения, как
(19)
При этом рекомендуется выполнить контрольный расчёт: если сумма всех ∑e¢i= 0 точно, то значения 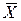и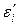 
найдены правильно.
Далее находится оценка СКО σ¢ ,т.е. средне-квадратическая погрешность (СКП) однократных измерений по известной формуле
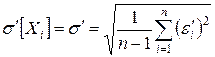, (20)
которую чаще используют в виде
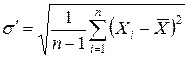(21)
Средне-квадратическая погрешность 
результатов n-кратных измерений 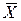, очевидно, должна быть меньше, чем σ¢ ,и оценивается соотношением¢
(21)
Таким образом, многократные измерения позволяют в 
раз уменьшить СКП по сравнению с единичными измерениями.
Отметим, что 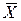и σ¢ являются состоятельными и несмещёнными оценками mx и σ при любых симметричных распределениях, а при нормальном распределении ещё и эффективными.
4.Оценка граничных значений случайной погрешности. Для нахождения граничного значения εг и 
погрешностей однократного и многократного измерений, надо знать коэффициенты tp и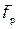 
, связывающие эти значения с соответствующими СКО (точнее - с оценками СКО):
(23)
Поскольку значения этих коэффициентов зависит от вида законов распределения результатов измерения Xi и 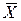, надо знать или хотя бы, обосновано предполагать конкретный вид этих законов (конкретные значения tp для наиболее распространённых законов мы уже определили раньше).
Для выяснения закона распределения результатов однократных измерений Xi – при их достаточном количестве – можно построить гистограмму, приближенно отображающую плотность распределения Xi (об этом несколько позже). Однако на практике характер закона распределения довольно часто можно обосновать физическими соображениями. Если, к примеру, ясно, что значения Xi симметрично флуктуируют в обе стороны около какого-то наиболее вероятного значения 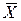, и вероятность появления Xi постепенно убывает с удалением от 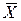, то такое распределение чаще всего соответствует нормальному закону.
А если, например, известно, что разброс Xi физически ограничен снизу и сверху некоторыми границами Xн , Xв , а внутри этих границ значения Xi равновероятны (как в случае погрешности квантования), то естественно принять, что закон распределения является равномерным. Заметим, что в этом случае, когда известны Хн , Хв , а значит и εГ = (Хв - Хн)/2, коэффициент tp требуется знать для оценки 
, которое может понадобиться для сложения погрешностей.
Рассмотрим подробнее наиболее распространённую ситуацию, когда однократные измерения, а значит и их случайные погрешности ε распределены по нормальному закону, который в общей (безразмерной) форме имеет вид
, (24)
где 
, и s - СКО, т. е. постоянное (не случайное) число.
В такой ситуации способ определения конкретных значений tp (а значит и εГ) несколько видоизменяется в зависимости от количества измерений n, с помощью которых найдена оценка σ¢. Здесь различают два случая.
Случай 1.Число n достаточно велико, а именно n>30. В таком случае можно считать, что найденная с помощью (20) оценка σ ¢» σ. и закон распределения (24) остаётся нормальным. Тогда для такого закона из таблиц находим уже известные нам значения tp. Например, tp=2 при доверительной вероятности Pt=0.95, tp=2.6 при Pt=0.99 и tp=3 при Pt=0.997. Умножив эти значения tp на σ/, найдём соответствующие граничные значения εГ доверительного интервала случайной погрешности однократных измерений:
-tpσ'<ε<tpσ' при заданной Рt (25)
Для n-кратных измерений доверительный интервал при той же Pt будет в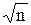 
раз ýже:
<
<
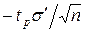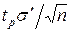(26)
Случай 2. Число измерений n<30. При этом приходится принимать во внимание, что в отличие от σ, σ¢ является случайной величиной (см.(21)). Следовательно, величина t= ε/σ/ , входящая в (24), теперь будет определяться соотношением двух случайных величин. При этом εi распределена нормально, а s¢, полученная на основе сложения квадратов нормально распределённых случайных величин Xi – 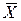(см. 21) , подчиняется c2 распределению с числом степеней свободы n – 1 (Это известно из теории вероятностей).
Из этой же теории известно, что в таком случае переменная t в (24) имеет уже не нормальное распределение, а распределение Стьюдента(аналитически оно записывается с использованием гамма-функций). Оно, подобно нормальному распределению, имеет максимум при t=0, симметрично относительно этого значения и асимптотически стремиться к нулю при t→∞. Однако, в отличие от нормального закона распределение Стьюдента зависит от числа n (рис. 2).
Рис. 2
Теоретически при n→∞,а практически при n>30 распределение Стьюдента совпадает с нормальным законом распределения. Для распределения Стьюдента взаимосвязь доверительной вероятности и безразмерного доверительного интервала tp также приводиться в таблицах (см. табл.1)
Таблица 1.
| n | tp | |
| Pt=0.95 | Pt=0.99 | |
| >30 | 2.6 | |
| 2.3 | 3.2 | |
| 2.8 | 4.6 |
Из рисунка и таблицы видно, что с уменьшением числа n многократного измерения доверительный интервал погрешности при одной и той же доверительной вероятности Pt расширяется. Это вполне понятно, поскольку с уменьшением n увеличивается разброс оценки σ ¢.
Найдя из таблиц значение tp для конкретных n и Pt , можно найти доверительный интервал случайной погрешности при однократных или многократных измерениях с помощью тех же соотношений (25), (26), что и в случае 1.