рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Приборостроение
- /
- Идентификация (определение) закона распределения результатов измерений
Реферат Курсовая Конспект
Идентификация (определение) закона распределения результатов измерений
Идентификация (определение) закона распределения результатов измерений - раздел Приборостроение, Повышение точности и оценка характеристик случайной погрешности В Нашем Случае, Термин Идентификация Подразумевает Процедуру Проверки ...
В нашем случае, термин идентификация подразумевает процедуру проверки гипотезы о соответствии (согласованности) предполагаемого закона распределения полученному ряду равнозначных измерений.
При достаточном количестве измерений (n>30) эту согласованность количественно оценивают путем сравнения гистограммы плотности распределения, полученной из экспериментальных данных, с аналогичной теоретической зависимостью предполагаемого закона, числовые параметры которого находят из тех же данных.
Для построения гистограммы:
1) Результаты измерений Х1, Х2, … , Хn располагают в порядке возрастания - в вариационный ряд Хmin, … , Хmax.
2) Диапазон результатов от Хmin до Хmax разбивается на определенное число интервалов m<<n с шириной каждого ј-го интервала dј=Xј-Xј-1 (Обычно интервалы выбирают одинаковой ширины d, за исключением случаев, когда результаты Xi располагаются в диапазоне Хmin … Хmax крайне неравномерно. В этом случае в области их наиболее плотного скопления приходится сужать интервал dј и наоборот.
3) Вычисляются количество nј и вероятность Pj попаданий Xi в каждый ј-й интервал:
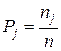 (1)
(1)
4) Оценивается плотность распределения в каждом интервале
 (2)
(2)
5) Строится соответствующая ступенчатая гистограмма 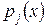 (рис.1).
(рис.1).
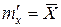 и σ' .
и σ' .
Теперь следует проверить правильность сделанного предположения – проверить гипотезу о законе распределения. Для этого разработаны специальные статистические критерии согласия экспериментальных данных с гипотетической теоретической зависимостью. Наиболее широко используется критерий χ2 Пирсона, при котором рекомендуется иметь n≥50. Критерий основан на вычислении количественного показателя Z, характеризующего степень расхождения вероятностей, полученных из экспериментальных данных и теоретической гипотетической зависимости:
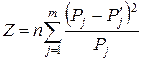 (3)
(3)
где  (4)
(4)
На практике, чтобы при расчете критерия (3) не иметь дело с дробными значениями Pj и 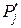 , удобнее использовать количество попаданий nj и n'j:
, удобнее использовать количество попаданий nj и n'j:
 ; где
; где 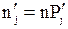 (5)
(5)
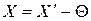 (10)
(10)
Но для упрощения процедуры исключения стандарт рекомендует использовать операции суммирования или умножения, используя, соответственно, поправку, равную (-Θ), или поправочный множитель αΘ:
 (11)
(11)
где 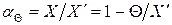 . Поправка или поправочный коэффициент могут быть представлены в виде графика (рис.3), таблицы или формулы.
. Поправка или поправочный коэффициент могут быть представлены в виде графика (рис.3), таблицы или формулы.
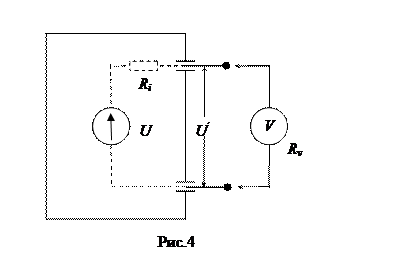
Очевидно, что измеренное значение 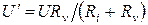 будет отличаться от измеряемого U. При этом
будет отличаться от измеряемого U. При этом
 (12)
(12)
С учетом Rv>>Ri (если это условие не соблюдается, погрешность будет слишком большой и измерение вообще недостоверно):
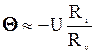
Соответственно, поправочный коэффициент

Очевидно, что при  погрешность Θ=0, а
погрешность Θ=0, а  . Если же, например,
. Если же, например,  =50
=50 , то относительная погрешность
, то относительная погрешность 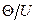 составит 2 %.
составит 2 %.
Отметим, что в приведенном примере для исключения погрешностей необходимо пользоваться поправочным множителем, а не поправкой (-Θ), в которую входит неизвестное (истинное) значение U.
Экспериментальное выявление систематической погрешностиможет
выполняться несколькими способами.
1. Использование образцовых средств измерения, систематическая погрешность 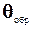 которых заведомо значительно меньше определяемой систематической погрешности
которых заведомо значительно меньше определяемой систематической погрешности 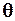 . Тогда, считая, что
. Тогда, считая, что  можно оценить
можно оценить 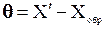 .
.
2. Рандомизация систематической погрешности — перевод систематических погрешностей в разряд случайных. Например, проводить измерение измеряемой величины несколькими приборами, у которых  будут различаться случайным образом. Тогда можно найти среднее значение измеряемой величины
будут различаться случайным образом. Тогда можно найти среднее значение измеряемой величины
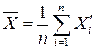 (13)
(13)
и тем самым снизить систематическую погрешность 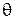 .(n – число приборов)
.(n – число приборов)
– Конец работы –
Эта тема принадлежит разделу:
Повышение точности и оценка характеристик случайной погрешности
Рис... оС со средним значением о рис При этом вполне естественно... Распространяя подобное рассуждение на другие составляющие независимые систематической погрешности можно найти...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Идентификация (определение) закона распределения результатов измерений
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов