Информационные характеристики измерения.

Очевидно, что при измерении мы получаем определенную информацию об измеряемой величине X. При этом возрастает определенность наших знаний о X. Иными словами, при измерении уменьшается неопределенность знаний об измеряемой величине. Клод Шеннон – основатель теории информации – предложил количественно выражать эту неопределенность так называемой энтропией.

В случае, если измеряемая величина X дискретна и может принимать ограниченное число N значений x_i с вероятностями их появления P_i, энтропия может быть выражена в виде

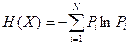(1)

Чем меньше число возможных значений N, тем меньше неопределенность знаний о X, и, значит, меньше энтропия H(X). В частности при N=1, P_i=1 и H(X)=0, т.е. неопределенность полностью отсутствует – значение X известно абсолютно точно.

Однако, на практике измеряемая величина X обычно непрерывна и поэтому даже в ограниченном диапазоне имеет бесконечное множество возможных значений x, отстоящих друг от друга на бесконечно малые расстояния dx с вероятностями появления P(X)=p(x)dx, где p(x) –плотность распределения вероятности. Распространяя на этот случай выражение энтропии (1), вместо операции сложения получим интеграл, в общем случае, в бесконечных пределах:

(2)

Представив (2) в виде суммы двух интегралов и учитывая, что

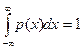, получим

(3)

Из (3) видно, что в случае непрерывной измеряемой величины энтропия Н(Х) бесконечна, т.к. в нем интегральное выражения конечно, а 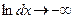. Физически это вполне понятно, поскольку число возможных значений Х бесконечно велико.

В частном случае, когда эти значения равновероятны и лежат в единичном интервале, энтропия . Следовательно, в (3) интегральное выражение

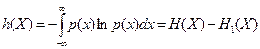(4)

Из (4) можно заключить, что h(X) есть энтропия непрерывной измеряемой величины, определяемая по сравнению с энтропией канонической величины, имеющей равновероятные значения в единичном интервале. Такая энтропия называется дифференциальной энтропией. Она используется для сравнительной оценки неопределенности знаний о непрерывной измеряемой величине.

Обычно до измерения известен лишь диапазон X_max-X_min измеряемой величины, внутри которого ее значения равновероятны и, следовательно, имеют постоянную плотность распределения (см. рис.1)

∆г

∆г

Рис. 1

Подставив это значение в (4), нетрудно определить (самостоятельно, пожалуйста) что априорная дифференциальная энтропия

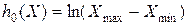(5)

Если погрешность измерения ∆=X'-X тоже имеет равномерное распределение p(∆) в пределах ∆_г, то после измерения зона неопределенности, очевидно, сузится до 2∆_г (рис.1), а дифференциальная энтропия соответственно уменьшается до значения

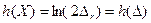,*⁾ (6)

где 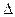=х - Х.

Количество информации Q_I получаемое в результате измерения, равно разности энтропий до и после измерения:

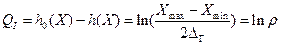(7)

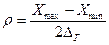где (8)

По своему физическому смыслу отношение ρ, очевидно, определяет число различимых градаций, т.е. число различимых ближайших значений измеряемой величины и называется разрешающей способностью средства измерения.

Из (4) и (5) следует, что чем меньше погрешность, тем больше получаемая информация и тем выше разрешающая способность прибора.

Важно отметить, что это заключение со всей очевидностью оказывается верным и при других законах распределения р(x) погрешности. Поэтому выражения (6), (7) и (8) можно распространить и на эти случаи, если заменить в них интервал 2∆_г на некоторый эквивалентный в отношении энтропии интервал неопределенности 2∆_э, приняв, что

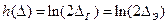(9)

Это фактически означает, что при произвольном распределении погрешности можно определить некий интервал неопределенности Х _э c таким же значением энтропии, что и в случае равномерного распределения. Граничное значение ∆_э такого эквивалентного интервала называют энтропийным значением погрешности. Это значение при произвольной плотности распределения p(x),

согласно (9), определяется соотношением

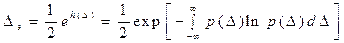(10)

 

Пояснение: В случаях, когда интервал неопределенности определяется погрешностью измерения, при определении энтропии (4) удобнее вместо текущей переменной х использовать переменную ∆=х-Х. Нетрудно показать, что при замене в (4) р(х) на р(∆) и dx на d∆, результат не меняется, т.е. h(x)=h(∆).

Найдем энтропийное значение погрешности, имеющей нормальное распределение

(11)

Найдя 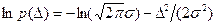и подставив это соотношение вместе с (11) в (10), с учетом того, что интеграл от 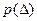в бесконечных пределах равен единице, а от 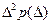- дисперсии , и принимая во внимание, что 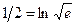, получим (получить самостоятельно:)

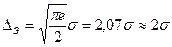(12)

Видим, что при нормальном распределении энтропийное значение погрешности , определяющее интервал неопределенности измерений, практически равно 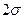, что хорошо согласуется с обычно используемым граничным значением =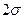доверительного интервала с вероятностью .

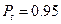Выполняя аналогичные действия, можно найти энтропийную погрешность для треугольного распределения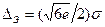

Очевидно, что для равномерного распределения .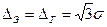

Достоинством энтропийного значения погрешности является то, что оно вполне однозначно определяет границы интервала неопределенности измерения в отличие от доверительных границ погрешности, которые зависят от выбранной доверительной вероятности. Энтропийная погрешность позволяет также при разных законах распределения погрешностей с единых позиций оценивать разрешающую способность прибора

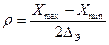(13)

и количество информации, полученное при измерении

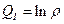(14)