рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Приборостроение
- /
- Приклади.
Реферат Курсовая Конспект
Приклади.
Приклади. - раздел Приборостроение, В передбачити точний результат процесу дуже важко, або навіть неможливо 1. Законами Ньютона Можна Описати Рух І Взаємодію Двох Тіл, А Для Трьох І Біл...
1. Законами Ньютона можна описати рух і взаємодію двох тіл, а для трьох і більше – ці методи вже не придатні.
2. Знаючи властивості водню та кисню, неможливо передбачити, що їх сполучення будуть мати невластиві їх елементам властивості.
3. Які наслідки могло дати повернення на південь сибірських річок, ідею якого пропонував ЦК КПРС?
Наука визнала фундаментальне положення про те, що властивості системи не зводяться до властивостей елементів, з яких вона складається. У зв’язку з цим, у науці почав розвиватися новий напрямок – системотехніка,або теорія систем. Термін система асоціюється з об’єктом складовим, який являє собою сукупність окремих елементів і в той же час об’єктом комплексним,окремі елементи якого функціонують у тісній взаємодії і складають одне ціле.
Існує багато визначень систем.
1. (Найкоротше) За визначенням Хола: „Система – це набір елементів, який включає взаємозв’язки між ними та їх ознаками”.
2. (Найповніше) „Система являє собою набір різних взаємодіючих людських і машинних елементів, об’єднаних для досягнення загальної мети шляхом маніпуляції та керування матеріалами, інформацією, енергією і людьми”.
Будь-яке визначення включає слово елементи, тобто об’єкти, з яких складається система. Віднесення того чи іншого об’єкта до складу елементів чи систем доволі умовне, тобто має відносний характер. Це пов’язано з тим, що у світі все пов’язано між собою. Для пояснення розглянемо такий об’єкт, як залізничний вагон. Це елемент чи система?
Відносно поїзда, вагонного парку, залізничного транспорту це їх елемент, а виходячи з конструкції самого вагона, який складається з великої кількості пов’язаних між собою окремих вузлів, - це складна система. У цьому проявляється подвійна суть будь-яких об’єктів у світі: кожен об’єкт можна розглядати як елемент у складі об’єкта вищого рівня, або як систему об’єктів нижчого рівня. Взагалі система являє собою багаторівневу конструкцію із взаємодіючих об’єктів, об’єднаних у підсистеми різних рівнів.
При вирішенні практичних задач діють таким чином: якщо поділення об’єкта на складові елементи впливає на показники функціонування, то його потрібно розглядати як систему. У випадку, коли поділення об’єкта на елементи не впливає на показники функціонування – його можна розглядати як елемент системи. Наприклад, при вирішенні задач організації роботи станції, вагон можна розглядати як елемент, оскільки поділення його на окремі складові (кузов, ходова части, гальмове обладнання, автозчеп) не впливає на показники роботи. І навпаки, спеціаліст-механік при вирішенні задач проектування чи ремонту вагонів буде розглядати вагон як систему.
Таким чином, система визначається не формальною кількістю об’єктів та її будовою, а тими задачами, які стоять перед дослідником або розробником, тобто залежить від мети. Іншими словами, об’єкт доцільно розглядати як систему, коли при його вивченні доводиться займатися взаємодією між елементами, тобто вирішувати комплексні загальносистемні питання.
Ознаки - це властивості елементів, тобто їх техніко-експлуатаційні характеристики, з допомогою яких можна визначити вплив елемента на показники функціонування системи. Як приклад можна привести потужність локомотива, його тягові та гальмові характеристики, параметри (довжина та ухил) залізничної колії, вантажопідйомність та габарити кузова вагона і таке інше.
Взаємозв’язки, або взаємодію елементів системи між собою можна розглядати як результат сукупності впливу кожного елемента на інші елементи. Як приклад можна розглядати взаємодію між вагонами в составі, між локомотивом та составом, між локомотивом та колією, між локомотивом та машиністом, між машиністом і черговим по станції і т.д. Взаємодія елементів системи між собою та з зовнішнім середовищем описується у математичному вигляді для можливості врахування і визначення показників функціонування.
Мета - означає такий стан системи, якого ми намагаємося досягти, або результати, які б ми хотіли мати. Мета грає найважливішу роль для системи. Лебідь, рак та щука разом з возом у відомій байці формально являють собою систему, яка має всі викладені вище ознаки - сукупність взаємодіючих елементів, але їх взаємодія не має загальної мети. Як наслідок, відсутній результат. Ось чому при дослідженні складних систем взаємодія елементів розглядається з позицій досягнення загальної мети. А мета, тобто те, що ми хочемо мати, може бути будь-яка, наприклад: швидше, дешевше, безпечніше, комфортніше і т.д.
Основні ознаки складних систем :
1. Наявність великої кількості взаємопов’язаних між собою об’єктів.
2. Складність функції, яку виконує система і яка спрямована на досягнення потрібної мети функціонування.
3. Можливість поділу системи на підсистеми, мета функціонування яких підпорядкована загальній меті системи.
4. Наявність управління, розгалуженої інформаційної мережі і потоків інформації.
5. Наявність взаємодії із зовнішнім середовищем і функціонування в умовах впливу випадкових факторів.
1.2 Етапи дослідження систем.
Накопичений досвід дослідження систем дозволив узагальнити основні етапи, які проходить дослідник будь-яких систем.
1. Постановка задачі і формулювання мети.
На цьому етапі розробник чи дослідник системи визначає мету її створення чи дослідження. Наприклад, для транспортних систем метою їх створення, дослідження чи удосконалення може бути:
- пошук оптимальних структур (будови) систем.
- пошук оптимальних параметрів технічного оснащення систем.
- визначення оптимальних параметрів функціонування (управління).
- розробка автоматизованих систем управління.
2. Формулювання критеріїв оцінки системи.
Під критеріями розуміють показники ефективності, тобто деякі числові характеристики системи, які оцінюють ступінь пристосування системи до вирішення поставлених задач. Критерій – це один з показників функціонування системи. Наприклад: обсяг роботи, швидкість руху, тривалість перевезень вантажів чи пасажирів, витрати на перевезення, прибуток від перевезень, продуктивність праці, собівартість продукції і т.д. Кожен з цих показників характеризує той чи інший бік діяльності системи. А щоб визначити найкращу до поставленої мети систему потрібно мати узагальнюючий критерій, який би враховував усі боки діяльності системи. Отже, мета і критерій між собою пов’язані, це різні сторони одного питання, а критерій – це кількісне вираження мети.
Критерії, які використовуються у системному аналізі, бувають: оптимізаційні, коли найкращий варіант рішення відповідає min або max значенню критерію; обмежувальні – за допомогою яких встановлюють діапазон бажаних значень критерію. Великі виробничі системи, як правило, багатокритеріальні.
Для транспортних систем найбільш поширеним узагальнюючим критерієм є витрати, який у числовій формі враховує максимальну кількість факторів. Але не всі показники можливо оцінити у вартісному вигляді: економія людського часу, вартість життя, екологічні наслідки, безпека руху.
Але загальний показник не завжди потрібен. Наприклад, в умовах перевантаження – слід визнати критерієм час, а не витрати. Тобто критерії можуть змінюватися у залежності від умов функціонування. Таким чином, визначення критерію оцінки системи становить першу задачу дослідження.
3. Аналіз системи
Аналіз, або декомпозиція системи – це поділ системи на компоненти, визначення факторів, що впливають на процес функціонування, встановлення взаємозв’язків між елементами. Уявимо собі, що для дослідження системи деякий критерій (добрий чи поганий – це інша справа) визначено. Тоді постає питання, як знайти краще рішення системи за допомогою цього критерію? Можна стверджувати, що величина вибраного критерію залежить від діючих на процес функціонування факторів, тобто його (критерій) можна вважати функціоналом, або функцією мети:
R = f (X1..Xk , Y1..Yk , Z1..Zk), (1.1)
де X, Y, Z – фактори, які впливають на процес функціонування.
Отримання такого функціоналу являє собою другу важливу задачу, яка є дуже складною. Складність отримання функціоналу полягає у великій кількості факторів, що впливають на процес (не всі з них виявлені, відомі і формалізовані), наявності залежності між факторами, наявності випадкових факторів. Наукові досягнення у цьому питанні відповідних галузей регламентуються як типові методики технічних розрахунків і з часом удосконалюються.
При вирішенні задач синтезу вважаються відомими структура системи та її конструктивні параметри, а потрібно визначити функціональні характеристики, тобто значення критерію ефективності.
4. Синтез системи.
Навпаки аналізу, задача синтезу системи полягає у визначенні структури, технічних і технологічних параметрів системи, згідно з встановленими величинами критеріїв ефективності. Якщо мати в явному аналітичному вигляді функціонал (1.1), то використовуючи різні математичні методи, можна визначити параметри X, Y, Z, які забезпечують оптимальне (R→ min або R→ max) значення критерію ефективності. На практиці такий підхід застосовується для обмеженого кола найбільш простих задач. Для більшості складних задач подібний (1.1) функціонал отримати неможливо. А як же вирішувати задачі (досягати мети) в умовах відсутності функціоналу? Це третя задача дослідження систем, для вирішення якої потрібен наступний етап.
5. Знаходження рішення.
В умовах відсутності функціоналу (1.1) для синтезу системи з відповідними показниками ефективності на практиці використовують різні неформальні методи. По суті всі вони зводяться до так званого перегляду варіантів, який можна назвати „синтезом через аналіз”. Зміст полягає у тому, що синтез системи здійснюється поетапно: дослідник намічає початковий варіант системи, з допомогою відомих методів аналізу визначає показники функціонування та ефективності. Потім намічається інший варіант системи, піддається аналізу і якщо функціональні характеристики не відповідають заданим, цикл операцій повторюється до тих пір, поки не буде знайдено варіант з потрібними характеристиками. Під час дослідження варіантів накопичуються відомості, які дозволяють виконувати цілеспрямований синтез, тобто вибирати для розгляду більш ефективні варіанти, не розглядаючи завідомо неефективні.
6. Впровадження рішення.
Для реальних систем результати досліджень впроваджуються в життя, для чого виконується розробка відповідного проекту.
1.3 Методи дослідження систем.
Для дослідження і оптимізації систем використовують два методи: експериментальний і розрахунковий.
Експериментальнийметод ґрунтується на дослідженні процесу функціонування діючих систем. Для цього будується початковий варіант системи на базі тих знань, які ми маємо про процес. У подальшому наглядом за процесом функціонування отримують потрібні показників, враховують виявлені недоліки, послідовно шляхом доробки та удосконалення доводять систему до потрібного стану.
До цього часу це було виправдано, бо людство мало справу з безпечними системами малої складності. Неточність розрахунків компенсувалась обсягом натурних експериментів, багаторазовою доводкою, запасом потужності, міцності. Тобто в обсязі дослідницьких робіт припадало 10% на розрахунки, а 90% - на експеримент.
Поява складних і небезпечних (пам’ятаєте Чорнобиль?) систем змінила співвідношення між розрахунковою і експериментальною частинами. Внаслідок ускладнення систем, експериментування з ними вимагає значних витрат коштів, часу і не завжди є безпечним (атомна енергетика, зброя). Це висуває на перший план потребу у розрахункових методах, розширення кола питань, які вирішуються розрахунковими методами.
В останні роки отримали розвиток нові наукові напрямки:
- теорія масового обслуговування;
- методи лінійного, нелінійного, динамічного програмування;
- теорія графів і мереж;
- методи планування експериментів;
- методи дослідження операцій.
Слід підкреслити, що системний аналіз не має своїх особистих методів, а використовує для вирішення системних завдань досягнення окремих розділів математики. Перелічені методи відносяться до класу розрахункових,за допомогою яких можливо виконати розрахунок показників ефективності, використовуючи формули та рівняння. Другим напрямком розрахункових методів є моделюванняпроцесу функціонування складних систем. При цьому використовують: графічне, аналітичне, графоаналітичне моделювання, або моделювання з допомогою ЕОМ.
1.4 Типи систем.
У науці виділяють 4 відокремлені системні напрямки:
1. Структурний (хімія, фізика, математика).
2. Системний (системотехніка, кібернетика).
3. Економіко-організаційний (економіка, управління, організація виробництва).
4. Загально-філософський (розглядання системи у плані логічних категорій „частина – ціле”).
Транспортні системи відносяться до економіко-організаційного напрямку.
2. ТРАНСПОРТНИЙ ПРОЦЕС ЯК СИСТЕМА.
2.1 Транспорт як галузь суспільного виробництва.
Термін транспорт походить від латинського слова transporto, що значить перевозити, переносити, переміщувати. В цьому полягає суть транспорту – переміщувати у просторі речовини, предмети, людей. Розглянемо роль цього процесу у житті людини, діяльності суспільства, існування держави.
Як відомо, діяльність людини поділяється на дві сфери: матеріального і нематеріального виробництва. Маркс і Енгельс про це говорять: ”Крім добувної промисловості, обробної промисловості та хліборобства існує ще четверта сфера матеріального виробництва – це транспортна промисловість, все рівно, перевозить вона людей чи вантажі”. І сучасна економічна наука не спростовує цього визначення. Таким чином, транспорт відноситься до сфери матеріального виробництва.
На відміну від перших трьох галузей сфери матеріального виробництва, транспорт не виробляє нових матеріальних продуктів, а тільки переміщує продукцію, створену в інших галузях матеріального виробництва. Транспорт відносять до сфери матеріального виробництва завдяки наступному. По-перше, транспорт безпосередньо приймає участь у процесі виробництва матеріальних благ, і є складовою частиною будь-якого виробництва (технологічний транспорт). По-друге, транспорт продовжує процес виробництва у сфері обігу, оскільки „товар тільки тоді готовий до споживання, коли він доставлений споживачу”. Першу задачу вирішує транспорт не загального користування, або промисловий, відомчий транспорт, який належить конкретному підприємству або галузі. Другу задачу вирішує транспорт загального користування, до якого і належить магістральний залізничний транспорт. Транспорт загального користування виконує в державі важливі економічні, політичні, соціальні, культурні і оборонні функції.
Цей транспорт згідно з законом України „Про транспорт” від 10.11.1994р „..є однією з найважливіших галузей суспільного виробництва і покликаний задовольняти потреби населення і суспільного виробництва в перевезеннях”. Головними завданнями підприємств і організацій транспорту є своєчасне, повне і якісне задоволення потреб у перевезеннях. При цьому необхідно забезпечувати:
- високу економічність роботи та зниження собівартості перевезень;
- скорочення термінів перевезень вантажів та пасажирів;
- безпеку руху транспортних засобів;
- виключення забруднення біосфери землі.
Інша особливість транспорту полягає в його продукції. Продукція транспорту являє собою завершене переміщення (перевезення) вантажів і пасажирів, і не має матеріального вираження, це, скоріше, філософське поняття. Вважається що продукція транспорту:
- виробляється і споживається одночасно, тобто існує тільки в процесі виробництва;
- її неможливо заощадити або резервувати про запас.
Ці особливості продукції транспорту ускладнюють управління транспортною галуззю, оскільки запас продукції створити неможливо, а в умовах коливання обсягів перевезень потрібно мати доцільні, економічно обґрунтовані резерви провізної та пропускної здатності, що являє собою складну інженерно-технічну задачу, яка на сьогодні не вирішена.
2.2 Визначення та елементи транспортної системи.
Транспортний процес - це процес переміщення у просторі транспортної маси - вантажів, людей, взагалі - об’єктів. Для забезпечення транспортного процесу необхідно мати:
1. Постійні пристрої і споруди (на прикладі залізничного транспорту): залізничну колію і станції, споруди для обслуговування пасажирів, пристрої навантаження, розвантаження і зберігання вантажів, пристрої АТЗ для управління, механізації та автоматизації виробничих процесів, пристрої для ремонту і обслуговування рухомого складу, пристрої водо- , енерго- та матеріально-технічного постачання.
2. Рухомий склад - локомотиви, вагони, МВРС.
3. Перемінні засоби - механізми, виконавці (ПТО, ПКО, машиністи, касири, провідники і т.д.).
4. Організаційну структуру для забезпечення управління транспортним процесом - ДСП, ДСЦ, ДНЦ, ДГП...).
Перелічені об’єкти - це елементи (або підсистеми) транспортної системи.
Таким чином, транспортна система - це сукупність елементів, які призначені для виконання сукупності операцій транспортного процесу.
2.3 Особливості транспортних систем.
Транспортна система має наступні особливості:
1. Велика кількість об’єктів (станції, дільниці, депо, пристрої СЦБ, вагони, локомотиви...), які взаємодіють між собою на великій території і функціонують по принципу конвеєра.
2. Велика кількість факторів, які впливають на процес функціонування (план, профіль дільниць, станцій, обсяги роботи, призначення вантажів, стан пристроїв), у тому числі і випадкові.
3. Складність аналітичного описання взаємодії і взаємовпливу факторів. Багато речей ще не досліджено і не має аналітичного опису.
4. Неоднозначність критеріїв оцінки системи (витрати, час, продуктивність, безпека руху), а також таких, що не формалізуються (безпека руху, конструкція горловин станцій).
5. Різнорідність операцій і різна тривалість їх виконання.
6. Постійна зміна умов функціонування.
7. Коливання обсягів роботи.
2.4 Причини, різновиди та показники нерівномірності перевезень.
Обсяги навантаження, розвантаження на станціях, передача вагонів між залізницями та їх дирекціями, розміри руху на дільницях не є сталими величинами, а змінюються між сезонами року, місяцями та декадами, по дням тижня і, навіть, годинами доби. Коливання обсягів роботи визнані неминучими, тобто розглядаються як об’єктивна реальність. Виділяють три групи причин нерівномірності роботи.
Економічні причини пов’язані з коливанням виробництва продукції, сезонністю виробництва, зміною зв’язків між районами виробництва і споживання і т.п.
Технічні причини пов’язані з коливанням розмірів вагонопотоків при відправленні їх з пунктів зародження або з технічних станцій у зв’язку з діючою системою організації вагонопотоків (планом формування поїздів), яка встановлює жорсткі вимоги до відправлення вагонів за їх кількістю та призначеннями.
Організаційні причини пов’язані з режимом роботи підприємств, перервами у вихідні та святкові дні, чи вночі, надання „вікон” для ремонту споруд і т.п.
Розрізняють наступні види нерівномірності.
Сезонна – зміна обсягів перевезень між періодами року (кварталами, місяцями), яку прийнято оцінювати коефіцієнтом нерівномірності:
 , (2.1)
, (2.1)
де – Qmax – максимальні обсяги перевезень за місяць;
Qср – середньомісячні обсяги перевезень.
Добова нерівномірність виникає внаслідок технічних і організаційних причин. Визначається як і сезонна, за формулою (2.1) за добовими обсягами роботи.
Внутрішньодобова нерівномірність виявляється у коливанні обсягів роботи між періодами доби (ніч-день) і навіть між годинами доби. Для оцінки нерівномірності цього виду використовують статистичні параметри: дисперсію, середнє квадратичне відхилення, коефіцієнт варіації інтервалів між подіями або кількості подій за одиницю часу.
Нерівномірність перевезень впливає на показники експлуатаційної діяльності залізниць та її технічне оснащення. Розглянемо цей вплив на таких прикладах.
Приклад 1. Тривалість знаходження рухомого складу на станціях значно збільшується при нерівномірному русі поїздів (рис. 2.1), тому що до тривалості обслуговування додається тривалість очікування обслуговування, яка відсутня при рівномірному русі.

Збільшення простою рухомого складу на станції збільшує тривалість його обігу, погіршує його використання, та збільшує робочий парк.
Приклад 2. За типовими методиками розраховують:
- площу складів для переробки вантажів  ;
;
- кількість механізмів для переробки вантажів  ,
,
де Q – річний вантажопотік;
tзб – термін зберігання;
p – навантаження на 1 м2;
R – продуктивність механізму.
Таким чином, збільшення нерівномірності перевезень негативно впливає на технічне оснащення і показники функціонування об’єктів.
2.5 Параметри транспортних систем.
Транспортна система характеризується трьома основними параметрами: завдання, структура, організація.
Завдання - або потреба (вимога) у переміщенні об’єктів. Завдання на перевезення визначається потребамиклієнтури і характеризується:
- видом та кількістю транспортної маси ;
- пунктом відправлення та призначення транспортної маси;
- терміном реалізації перевезень.
Структура - це вид і кількість елементів, які визначають технічне оснащення і обслуговуючий персонал системи. Структура характеризує будову (архітектуру, топологію) системи і дає загальний опис елементів, з яких складається система, а також взаємозв¢язок між ними. При цьому розрізняють організаційнуі технічну структуру.
Під організаційноюструктурою розуміють форму розподілу задач і повноважень по формуванню рішень між людьми, які утворюють структурні підрозділи системи. Приклади організаційних структур: структура управління залізничним транспортом України (рис. 2.2), структура управління залізничною станцією або іншим структурним підрозділом.
Технічна структура - сукупність елементів, що приймають участь у технологічному процесі функціонування системи. Приклади технічної структури: топологія мережі, схема залізничного вузла, станції (рис. 2.3).

Організація. Вимоги на перевезення, визначені завданням, повинні бути ефективно реалізовані, що вимагає підготовки відповідного плану взаємодії елементів системи у часі, тобто організації. У самому загальному вигляді план організації роботи системи відповідає на питання: хто, що, коли і деповинен робити. Для пояснення, що мається на увазі під взаємодією, розглянемо приклад.
Треба перенести важку балку групою робітників. Взаємодія людей полягає у синхронізації: моменту підйому, під час руху (напрямок, швидкість), моменту опускання. Чим більш точно синхронізовані їх дії, тим менші витрати праці потрібні для перенесення балки, або тим більшу балку вони зможуть перенести. Слід підкреслити, якщо витрати на реалізацію завдання більші, ніж сума витрат при незалежних діях елементів, - це ознака того, що елементи взаємно заважають один одному – протидіють ( лебідь, рак і щука). Чим краще взаємодіють елементи, тим менші витрати на реалізацію завдання.
У транспортній системі організація перевезень підпорядкована графіку руху поїздів а також технологічними процесами роботи станцій. Послідовність елементів технологічного процесу повинна бути синхронізована у часі. Це приведе до min простою поїзда, тобто до min витрат.
Таким чином, транспортну систему можливо визначити як організовану сукупність елементів. А основою взаємодії елементів є технологія процесу перевезень. Основна задача полягає у визначенні оптимальних (за вибраним критерієм) параметрів: технічної структури, організаційної структури та організації роботи. Для цього потрібно робити відповідні дослідження.
2.6 Типи транспортних систем
У загальному випадку, враховуючи вид об’єктів, які є предметами транспортування, можна розрізнити два випадки.
1. Об’єкти, у переміщенні яких зацікавлене суспільство. Такі перевезення піддаються управлінню з точки зору досягнення будь-яких суспільних потреб. Як правило, критерієм ефективності постають витрати у сукупності на всі перевезення:
∑Мі·Сі → min,
де Мі - транспортна маса;
Сі – собівартість перевезення одиниці транспортної маси окремої відправки.
При цьому вирішуються такі задачі:
- раціональне закріплення поставників і споживачів;
- розподілення потоків за маршрутами з урахуванням завантаження окремих елементів;
- виключення зустрічних перевезень.
Подібні задачі вирішуються транспортом загального користування, який отримав назву нормативна система.
2. Об’єкти переміщуються самостійно, і переміщуються між тільки їм відомими пунктами за індивідуально визначеними маршрутами. Ці об’єкти поводять себе на свій розсуд, виходячи з особистого розрахунку. Критерії можуть бути різні (min час, шлях, витрати чи, навіть, якість дороги, її естетичний вигляд). Такі об’єкти також являють транспортну систему, яка отримала назву дескриптивнасистема, її представляють приватні транспортні засоби.
Функція мети може бути визначена як Ri → min,
де Rі – значення критерію окремого об’єкта.
На перший погляд, при Ri = min, отримаємо ∑R = min, але при цьому випускаємо з виду взаємодію об’єктів між собою. Наприклад, якщо кожний об’єкт бажає здійснити поїздку за мінімальний час (t → min), то збільшення потоку на трасі приводить до значного зростання кожного tі і величини ∑t. У нормативній системі ми могли б регулюванням зменшити ∑t.
3. ВИМІРНИКИ ТРАНСПОРТНИХ ПРОЦЕСІВ
3.1 Основні одиниці вимірювання
Система одиниць у фізиці базується на декількох основних одиницях вимірювання, а саме: маса, шлях, час. Транспортні процеси відбуваються згідно з фізичними законами, але при їх описуванні слід брати до уваги додаткову інформацію, що знаходиться за межами фізики: пасажири і вантажі, що підлягають перевезенню, не абстрактні і не взаємозамінні. Тому закони і величини, які застосовуються у фізичній теорії, недостатні для описування транспортної теорії. Для неї потрібні особливі вимірники, які б відображали процеси і явища, що відбуваються.
Система транспортних вимірників ґрунтується на базі трьох основних одиниць: транспортна маса (М), транспортний шлях (L), транспортний час (Т).
Транспортна маса являє собою кількість одиниць, які транспортуються або підлягають транспортуванню. У залежності від виду одиниць, що транспортуються транспортна маса може визначатися в різних одиницях вимірювання:
- у тонах для вантажів (вугілля, зерно);
- у штуках для вантажів (місця, контейнери);
- кількість пасажирів;
- кількість вагонів;
- кількість поїздів.
Таким чином, транспортна маса не є абсолютно фізичною величиною, і має різні вимірники. Тому неможливо додавати кількість пасажирів, контейнерів, вагонів або поїздів для визначення загальних обсягів перевезень.
Транспорту масу можна розглядати як скаляр або вектор.
Скалярна транспортна маса складається з одиниць, для яких нічого невідомо про напрям перевезення. Поки невідомий напрям, невідомий і час (момент) перевезень. Наприклад, вугілля на складі, про яке ще невідомо напрям перевезень.
Векторнатранспортна маса просторово-часову інформацію про пункт відправлення і пункт призначення, про момент і термін перевезення. Векторна ТМ не має інформації про шлях, що пройдений та тривалість перевезення, тому є величиною статичною.
Транспортний шлях розглядається як відстань між пунктами відправлення та призначення транспортної маси. При цьому розрізняють (рис. 3.1): повітряний шлях (Lп), тарифний (найкоротший) шлях (Lт), експлуатаційний (дійсний) шлях (Lе). Одиниці вимірювання транспортного шляху мають лінійні розмірності (км, м).

Транспортний час – проміжок часу, необхідний для реалізації процесу перевезень. При цьому розрізняють: тривалість ходу – проміжок часу, коли транспортна маса знаходиться у стані руху, тривалість перевезень – враховує тривалість ходу, а також тривалість усіх стоянок для виконання технологічних операцій і очікувань. Для вантажних перевезень термін їх здійснення має назву „Термін доставки”.
Одиниці вимірювання транспортного часу – загальноприйняті : секунда, година, доба, місяць, рік. Особливість полягає у відліку початку робочої доби – 17.00 за Київським часом.
3.2 Показники (вимірники) транспортної роботи.
З трьох основних одиниць вимірювання М, L, Т утворюються похідні вимірники, які використовуються для характеристики окремого боку транспортного процесу. У кваліметрії похідні показники визначаються функцією:
R = M x · L y · T z
Наприклад, для х = 0, у = 1, z = -1, маємо R = M 0· L 1 · T -1 = L / T = V (швидкість).
Для характеристики транспортних процесів використовують показники, які класифікуються наступним чином: технічні і економічні, кількісні і якісні, абсолютні і відносні. Розглянемо деякі найбільш поширені показники.
Потужність потоку, або транспортна маса, що підлягає перевезенню між окремими пунктами в одиницю часу:
Р = М / Т. (х = 1, у = 0, z = -1)
На базі цього вимірника ґрунтуються такі показники:
- перевезено (відправлено) вантажів (∑Р т/добу, тис.т/місяць, ∑N вагонів/добу, вагонів/ місяць);
- перевезено (відправлено) пасажирів (∑А тис. пас./добу, пас/рік).
- робота залізниці (дирекції) – кількість завантажених вагонів власного завантаження Nзв та прийнятих Nзп від сусідів U = Nзв + Nзп (вагонів/добу).
Це технічні, кількісні, абсолютні показники.
Швидкість руху, тобто відстань, яку проходить транспортна маса в одиницю часу:
V = L / T. (х= 0, у = 1, z = -1 )
Це технічний, якісний, відносний показник. В теорії та практиці роботи залізничного транспорту розрізняють наступні різновиди швидкості: конструкційна, максимально допустима, розрахункова, ходова, технічна, дільнична, маршрутна.
Транспортна робота.
Транспортна маса, перевезена з пункту відправлення в пункт призначення, являє собою виконану транспортом роботу. За аналогією з фізикою, де робота визначається як
Аф = F·S, ( F – діюча сила, S – шлях),
транспортна робота визначається аналогічно: Атр = M·L, (х = 1, у = 1, z = 0), але має принципові відмінності від механічної роботи.
Транспортна робота визначається окремо за видом перевезень і має відповідну назву:
- вантажообіг визначається для вантажних перевезень як сума добутків кількості перевезених вантажів на відстань перевезень (∑Q·L) за певний період (добу, місяць, рік) і вимірюється в ткм; при цьому розрізняють вантажообіг брутто і нетто;
- пасажирообіг визначається для пасажирських перевезень як сума добутків кількості перевезених пасажирів на відстань перевезень (∑А·L) за певний період (добу, місяць, рік) і вимірюється в пас·км;
- приведений вантажообіг визначається як сума вантажообігу та пасажирообігу і вимірюється в приведених ткм ∑Q·Lпр = ∑Q·L + ∑А·L.
Це кількісні абсолютні показники обсягів роботи дільниць, дирекцій, залізниць, транспорту в цілому.
 Чисельно механічна і транспортна робота суттєво відрізняються, бо сила, що прикладена вздовж напрямку переміщення (F) не дорівнює вазі (М). Для пояснення розглянемо випадок руху поїзда на підйомі траси залізничної лінії (рис. 3.2). Визначимо механічну роботу, яку здійснює локомотив для переміщення поїзда на відстань L: Aмех= FтL,
Чисельно механічна і транспортна робота суттєво відрізняються, бо сила, що прикладена вздовж напрямку переміщення (F) не дорівнює вазі (М). Для пояснення розглянемо випадок руху поїзда на підйомі траси залізничної лінії (рис. 3.2). Визначимо механічну роботу, яку здійснює локомотив для переміщення поїзда на відстань L: Aмех= FтL,
при цьому для руху без зниження швидкості повинна витримува-тися умова: Fт ≥ W + Fi.
Визначимо числові значення для умов: і = 8‰; M = 4000 тс;
L = 1 км, питомий опір руху становить w = 2 кгс/тс.
W = w M = 2∙4000 = 8000 кгс; Fi = і M = 8∙4000 = 32000 кгс.
Aмех= (8000+32000)∙1∙10-3 = 40 тс∙км
А величина транспортної роботи дорівнює Aтр= МL = 4000∙1 = 4000 тс∙км
Отже, транспортна робота набагато перевищує механічну, не є реалізованою механічною роботою, а являє собою умовний показник, і їх не можна ототожнювати.
Для зацікавлених, дайте відповідь, чому дорівнює механічна робота у випадку руху поїзда у зворотному напрямку?
Обіг вагона – це проміжок часу між двома однаковими станами вагону. Прийнято рахувати обіг вагона (Θ) як час між суміжними операціями навантаження (рис. 3.3). Обіг вагона є технічним, якісним, абсолютним показником використання рухомого складу у часі.
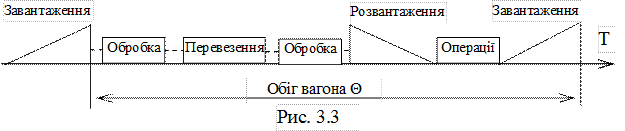
За змістом обіг вагона характеризує середню витрату часу на здіснення одного перевезення. Чим менше обіг вагона, тим менше вагонів потрібно для виконання певного обсягу роботи. Ця залежність являє собою за змістом основний закон транспорту і може бути подана в аналітичному вигляді наступним чином:
Np=U Θ,
де Np – робочий парк рухомого складу;
U – обсяг роботи за добу;
Θ – обіг рухомого складу, виражений в добах.
Підвищення швидкості руху поїздів, зменшення тривалості простою на станціях під операціями та в очікуванні їх виконання зменшує величину обігу вагона, покращує якість його використання та зменшує потреби у робочу парку вагонів для перевезення певної кількості вантажу.
Розглянемо приклади використання цього закону.
Приклад 1. Транспортна система щодобово повинна забезпечувати завантаження і перевезення 240 вагонів. Середній обіг вагона становить 36 годин. Для такої системи потреба у рухомому складі становить: Np = 240·36/24 = 360 вагонів.
Приклад 2. Добовий обсяг роботи дирекції залізничних перевезень становить U=1000 вагонів, а обіг вагона Θ = 2,8 доби. За рахунок удосконалення технології роботи скорочено обіг вагона на 3 години. Скорочення обігу вагона викликає скорочення потреб у рухомому складі, у зв’язку з чим економія, або визволення для додаткової роботи, робочого парку становить: ΔN = Np1- Np2 = 1000·2,8 - 1000·(2,8 – 3/24) = 125 вагонів.
Час простою вагонів на станціях.
Тривалість знаходження вагонів на станціях від моменту їх прибуття до моменту відправлення є одним з технічних, якісних, абсолютних показників. У залежності від категорій вагонів виконується нормування, ведеться облік і звітність простою транзитних вагонів (з переробкою, без переробки) та місцевих вагонів (з одною та двома вантажними операціями). Тривалість простою є складовою обігу вагона, і її скорочення має економічний ефект.
Відносні показники.
Вантажонапруженість – вантажообіг, що приходиться на 1 км залізничної лінії, показує інтенсивність використання технічних засобів і визначається як
Г = ∑QL/Le (ткм/км),
де Le - експлуатаційна довжина залізничної лінії.
Продуктивність праці П = ΣM·L/N (ткм/чол).
Собівартість перевезень С = Е/M·L (коп./ткм).
Питомі витрати е = В/M·L (палива/ткм, кВт/ткм, ресурсів/ткм).
Ці економічні показники використовують для аналізу і планування виробництва при визначенні: нормативів чисельності штату, матеріального забезпечення.
Тут розглянуто основні, найбільш поширені показники роботи транспортних систем. Більш детально показники розглядаються у спеціальній літературі.
4. ПОТОКИ ПОДІЙ ТА ЇХ ПАРАМЕТРИ
4.1. Поняття та різновиди потоків.
Під потоком подій розуміють послідовність подій, які відбуваються одна за одною у будь-які моменти часу. Такий потік можна подати у вигляді ряду точок Т1, Т2 .... Тn на числовій осі Т, які відповідають моментам появи подій 1, 2, .. n (рис. 4.1).

Приклади потоків подій: моменти прибуття поїздів, моменти завершення обробки, моменти закінчення розпуску.
У транспортних системах зустрічаються різні види потоків.
Регулярний потік - у якому події відбуваються з визначеними, суворо сталими, однаковими інтервалами I1 = I2 = In.
Регулярні потоки у транспортних системах дуже рідкісні. Близькими до них є потоки поїздів метрополітену, і то на протязі деякого часу, а не протягом доби.
Потоки подій, у яких інтервали відрізняються між собою, у загальному випадку називають випадковими. Серед різноманітніх випадкових потоків окремо виділяють потік, який називають найпростішим, і який має наступні властивості: стаціонарність, ординарність, відсутність післядії.
Стаціонарність - ймовірність появи m подій за час t залежить від величини t і не залежить від того, де на числовій осі Т розташований відрізок t. Зверніть увагу, що постійна не кількість подій m, а ймовірність появи цієї кількості, тобто Рm(t) =const.
Розглянемо процес прибуття поїздів на станцію. В окремі періоди більше пасажирських, менше вантажних, отже на протязі доби умова стаціонарності не дотримується. З цього приводу відомий вчений Вентцель Е.С. висловлюється: „Так обстоит дело со всеми физическими процессами, которые называют стационарными: в действительности они стационарны на отдельных отрезках времени. Распространение этого участка до бесконечности - лишь удобный прием, применяемый в целях упрощения анализа”.
Ординарність - ймовірність здійснення 2-х і більше подій за елементарний проміжок часу Dt®0 зневажливо мала порівняно з ймовірністю здійснення одної події. Це означає, що події здійснюються поодиноко, тобто Р(m>1) t®0=0.
Чи може на станцію за годину прибути більше двох поїздів? Очевидно, що може, отже потік не ординарний? А за 1 хвилину? Може, але дуже рідко. А за 1 сек? Можливо, але ймовірність така мала (навіть з декілька підходів), що нею можна зневажати, тобто вважати потік ординарним. А можливі і неординарні потоки, наприклад, потік вагонів на сортувальні колії (в один момент може на окрему колію поступити у відчепі більше двох вагонів. Отже цей потік вже неординарний, а потік відчепів на сортувальні колії – ординарний, тому що два або більше відчепи за малий проміжок часу поступити на колію не може..
Відсутність післядії - події відбуваються незалежно одна від одної. Ймовірність здійснення m подій за деякий час t2 не залежить від того, скільки подій відбулося за попередній відрізок часу t1.І навпаки – якщо кількість подій у майбутньому (за відрізок часу t2) залежить від того, скільки подій відбулося у попередній відрізок часу t1 – це наявність післядії m2=F(m1).
Якщо розглядати прибуття поїздів на станцію з одного напрямку, то такий потік володіє деякою післядією - після прибуття поїзда протягом мінімального інтервалу попутного слідування (t = Imin) поїздів не буде. Зникла випадковість, з¢явилась деяка (обмежена у часі) закономірність. А після (Imin) процес знову набирає випадковий характер.
Потоки, у яких не витримується хоча б одна з вказаних властивостей – це складні випадкові потоки. Потрібно ще раз підкреслити, що найпростіший - це випадковий потік. А назва його походить від того, що його математичний опис - найпростіший серед довільних випадкових. Розглянуті вище окремі приклади транспортних потоків показують, що в транспортних системах можуть бути як найпростіші так і інші випадкові потоки.
4.2. Параметри потоків.
Потоки можуть характеризуватися як моментами здійснення подій так і інтервалами між суміжними подіями (І, на рис. 4.1). Для регулярного потоку основним параметром є величина інтервалу між подіями I =const. На базі цього інтервалу можна визначити інший параметр потоку - інтенсивність, тобто кількість подій в одиницю часу, який розраховується
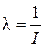 .
.
Наприклад, величина інтервалу у регулярному потоці становить I=15 хв = 0.25 год. Тоді l=1/15=0.0667 поїздів/хв, або l=1/0.25=4 поїзда/год.
Знаючи параметри такого потоку, маємо можливість виконати розрахунки:
- моменту звершення будь-якої події: Тn=T1 + (n-1)I ;
- кількості подій за деякий час t: m = t/I = lt.
Запитання. Здійснюється одна подія за добу в моменти часу: вчора - о 10-й год, сьогодні - об 11-й год, завтра - о 12-й год і т.д. Потік цих подій регулярний, чи ні? Інтервали між подіями є постійними і становлять 25 годин, отже потік регулярний.
У випадкових потоків інтервали між подіями є випадковими величинами, тому для характеристики і математичного опису випадкових потоків використовують параметри розподілу випадкових величин. З використанням даних статистичних спостережень ці параметри розраховують наступним чином:
- математичне очікування інтервалу між подіями 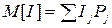 ; (4.1)
; (4.1)
- дисперсія інтервалів  або
або 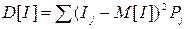 ; (4.2)
; (4.2)
- середнє квадратичне відхилення інтервалів 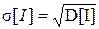 ; (4.3)
; (4.3)
- коефіцієнт варіації інтервалів (вхідного потоку)  ; (4.4)
; (4.4)
- середня інтенсивність потоку  . (4.5)
. (4.5)
Для випадкових потоків, окрім параметрів розподілу інтервалів, визначають закон їх розподілу, від якого залежать показники функціонування системи. Закони розподілу наведені в спеціальній літературі і тут не розглядаються. Одним з таких законів є „показниковий” або експоненціальний, який має характерну особливість:  . Як наслідок, коефіцієнт варіації вхідного потоку у випадку експоненціального закону розподілу інтервалів дорівнює
. Як наслідок, коефіцієнт варіації вхідного потоку у випадку експоненціального закону розподілу інтервалів дорівнює
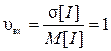 .
.
Теоретично доведено, що у найпростішому потоці інтервали між подіями розподілені за експоненціальним законом, тому такий потік має υвх = 1,0. Отже, при вирішенні задач, належить звертати увагу на умови задачі. Якщо сказано в умові, що вхідний потік найпростіший, або інтервали у випадковому вхідному потоці розподілені за експоненціальним (показниковим) законом, це свідчить, що υвх = 1,0. Справедливе і зворотне твердження: якщо інтервали у потоці мають коефіцієнт варіації υвх = 1,0, то вхідний потік – найпростіший.
І навпаки, у випадку регулярного потоку, коли усі інтервали становлять однакову величину, середнє квадратичне відхилення становить 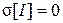 , тоді коефіцієнт варіації дорівнює
, тоді коефіцієнт варіації дорівнює
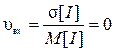 .
.
Таким чином, знаючи коефіцієнт варіації вхідного потоку, можна робити наступні висновки: υвх= 0 – потік регулярний, υвх= 1 – потік найпростіший, 0< υвх <1 – потік випадковий довільний.
5. ТЕХНОЛОГІЧНИЙ ПРОЦЕС ФУНКЦІОНУВАННЯ ТРАНСПОРТНОГО ОБЄКТА
5.1 Формалізація технології роботи об’єкта.
Технологічний процес визначає перелік операцій, їх послідовність, тривалість і порядок використання елементів. Виробничий процес при складанні технології розчленяють на події і роботи.
Подією називають факт закінчення одної або декіка робіт (операцій). Наприклад: прибуття поїзда, закінчення обробки, закінчення розформування.
Роботою (операцією) називають виробничий процес, який вимагає витрат часу і праці. Наприклад: обробка, розформування, формування і т.і.
Робота, яка не потребує витрат праці, але потребує часу, називається очікуванням.
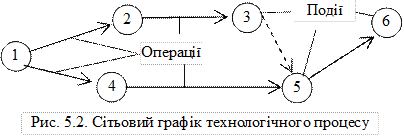
Будь яка складна послідовність робіт може бути подана у графічному вигляді: стрічковим (рис. 5.1) або сітьовим графіком (рис. 5.2).
З метою розрахунку показників функціонування та можливості дослідження процесів доцільно подавати технологію у вигляді функціональної схеми, приклад якої наведено на рис. 5.3.
| №№ пп | Операції | Тривалість виконання | Час і послідовність виконання операцій | Виконавці |
| Операція 1 |  t1 t1
| А | ||
| Операція 2 | t2 | Події | Б | |
| Операція 3 | t3 | В | ||
| Операція 4 | t4 | Г | ||
| Операція 5 | t5 | А | ||
| Загальна тривалість |
Рис. 5.1. Стрічковий графік технологічного процесу.

5.2 Механізми та параметри процесу обслуговування.
Під обслуговуванням будемо розуміти виконання будь-яких операцій з окремими заявками потоку. Наприклад: обробка составів бригадою ПТО, розпуск состава з гірки, обробка документів, закріплення рухомого складу, завантаження вагонів тощо. Механізм обслуговування характеризує тривалість виконання операцій. У залежності від факторів, які впливають на тривалість обслуговування, розрізняють наступні механізми обслуговування.
1. З постійною тривалістю обслуговування, незалежно від будь-яких факторів процесу, тобто tобс = const. Знаючи tобс, можливо визначити:
- інтенсивність обслуговування, тобто кількість заявок, які можуть обслуговані за одиницю часу  ;
;
- кількість заявок, які можуть бути обслуговані за деякий час Т N = μT.
Такий механізм обслуговування зустрічається в транспортних системах дуже рідко. Близькі до нього такі операції як розвантаження вагонів на вагоноперекидачах, зважування вагонів, тобто такі операції, на які впливає мала кількість факторів.
2. З тривалістю обслуговування, яка залежить від деяких параметрів заявок чи пристрою обслуговування. Прикладами такого механізму обслуговування можуть бути:
- тривалість розпуску состава з гірки 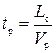 , (5.1)
, (5.1)
де Lc – довжина состава;
Vp – швидкість розпуску;
- тривалість обробки состава бригадою ПТО 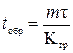 , (5.2)
, (5.2)
де m – кількість вагонів у складі поїзда;
τ – тривалість обслуговування одного вагона;
Kгр – кількість груп у бригаді ПТО;
- тривалість осаджування вагонів на сортувальних коліях tос = 0,06mc (5.3)
- тривалість маневрового напіврейсу tм = a + bmc , (5.4)
де a, b – коефіцієнти, які залежать від довжини маршруту, виду локомотива, стану гальм (увімкнуті, вимкнуті).
Вирази (5.1), (5.2) є фізичними, оскільки відтворює фізичний зв’язок між діючими фактьторами, а формули (5.3) і (5.4) є емпіричними, які отримані штучним шляхом, дозволять розрахувати потрібні показники, але не відображають фізичний зв’язок між діючими факторами. Більш того, останні формули дають приблизний результат, тому що враховують далеко не всі фактори, від яких залежать показники функціонування. Наприклад, чим вища гірка тим далі скочуються вагони, тим менше повинна бути тривалість осаджування, але цей фактор вираз (5.3) не враховує. Чи залежить тривалість подачі-прибирання вагонів від їх ваги, або ухилу колії? Напевно залежить, а ці фактори (5.4) не враховує.
Таким чином, будь-які формули для розрахунку показників процесу є приблизними, тому що не враховують усіх факторів. Інша їх особливість полягає у тому, що з їх допомогою можна розрахувати середню (математичне очікування) тривалість виконання операцій, а в дійсності вони будуть відрізнятися від розрахункових. Це пов’язано з тим, що враховані не всі фактори, а також з наявністю випадкових факторів, величини яких заздалегідь невідомі, наприклад: питомий опір руху вагонів, опір середовища та вітру, тощо.
3. З випадковою тривалістю обслуговування. Якщо тривалість обслуговування заявок є випадковою величиною, то для її характеристики використовують наступні параметри:
- математичне очікування тривалості обслуговування 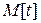 ;
;
- дисперсія тривалості обслуговування 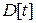 ;
;
- середнє квадратичне відхилення тривалості обслуговування  ;
;
- коефіцієнт варіації тривалості обслуговування (вхідного потоку)  ;
;
Параметри розподілу тривалості обслуговування розраховують за статистичними даними з допомогою виразів, аналогічних (4.1- 4.4). У деяких випадках, коли випадкова величина є функцією інших випадкових величин t = f(x, y), і відомі параметри розподілу аргументів M[x], σ[x], M[y], σ[y], є можливість розрахувати параметри функції M[t], σ[t] аналітично, користуючись формулами, виведеними для окремих функцій і наведених у підручниках по теорії ймовірностей. Для повноти інформації про механізм обслуговування визначають також закон розподілу тривалості обслуговування.
Для практичного використання, необхідно засвоїти, що у разі розподілу випадкової величини за показниковим (експоненціальним) законом, коефіцієнт варіації тривалості обслуговування дорівнює  , а у випадку обслуговування заявок з постійною тривалістю коефіцієнт варіації становить
, а у випадку обслуговування заявок з постійною тривалістю коефіцієнт варіації становить  .
.
5.3 Дисципліна обслуговування заявок.
Під дисципліною обслуговування розуміють порядок вибору заявок на обслуговування. Взагалі розрізняють наступні види обслуговування.
1. У порядку черги надходження в систему (перший прибув – перший обслуговується). Такий порядок вибору найбільш справедливий та найпростіший з точки зору математичного опису і поширений у діяльності транспортних систем. Наприклад, обробка, розформування поїздів частіше всього здійснюється за цим порядком. Але слід зауважити, що не завжди такий порядок є доцільним за умови ефективності.
Наприклад, маємо у парку прийому два готових до розформування поїзда. У складі одного з них є вагони, якими можна завершити процес накопичення нових составів на сортувальних коліях, це так звані состави із замикаючими групами. У складі іншого поїзда відсутні замикаючі групи. Який состав на ваш погляд доцільно розформувати у першу чергу? Очевидно, що состав із замикаючими групами, зневажаючи тим, хто з них прибув першим. Отже, може існувати і інший порядок виру на обслуговування.
2. Обслуговування з пріоритетами. У цьому випадку заявки вибираються на обслуговування згідно з їх пріоритетами, тобто згідно з ступінню заявок класифікації за деякими ознаками.
У попередньому прикладі ознакою класифікації була кількість замикаючих груп у складі: чим більше замикаючих груп, тим вищий пріоритет на першочергове обслуговування.
Інший приклад: у разі перетинання маршрутів слідування поїздів порядок їх пропуску визначається згідно з їх рангом: вищий ранг – пасажирські, середній ранг – вантажні, нижчий ранг – маневрова робота. А при заявках одного рангу завжди можливо визначити додаткові ознаки, за якими приймається рішення про черговість обслуговування. Наприклад, з двох вантажних поїздів перевага надається тому, що прибуває, або більш важкому, і таке інше з безлічі можливого.
3. Випадковий вибір на обслуговування, коли з декілька заявок, які претендують на обслуговування, черговість визначається випадковим чином – навмання. Такий порядок у практиці може мати місце, але тільки у випадку, коли черговість зовсім не впливає на показники функціонування. Наприклад, токар на верстаті виконує обробку металевих заготовок, які з штампувального верстата подаються до коробки. Чи має значення, у якому порядку виконується їх обробка? Чи впливає порядок обробки на кінцеві показники? Очевидно, що ні, тому такий порядок у практиці може існувати.
У транспортних процесах завжди з декількох варіантів можливо вибрати більш ефективний за тими чи іншими ознаками, який принесе більшу загальну користь, ніж приймати рішення випадковим чином. А для цього існують як писані правила (ранг поїздів), так і не писані, які працівники опановують на своєму досвіді, або досвіді попередників.
Слід зауважити, що дисципліна обслуговування впливає на математичний опис процесів і на показники функціонування. Наприклад, тривалість затримок в пунктах перетину маршрутів буде відрізнятися у залежності від того маршрути рівноправні, чи нерівноправні. Теорія цього питання розглядається у курсі Залізничні станції та вузли.
6. ЕКСПЛУАТАЦІЙНІ ПОКАЗНИКИ ФУНКЦІОНУВАННЯ ТРАНСПОРТНИХ ОБЄКТІВ
6.1. Процес функціонування об’єктів та його різновиди.
Якщо з часом у системі відбувається зміна будь-яких техніко-експлуатаційних характеристик, говорять, що відбувається процес функціонування. І навпаки, якщо характеристики з часом не змінюються, процес не відбувається. Для будь-якої фізичної системи можливо застосувати поняття її стану. Під станом розуміють деяку характеристику системи у довільний момент часу.
Наприклад, для такої системи, як людський організм, існує дуже велика кількість параметрів (характеристик), за якими оцінюється стан системи. Це і тиск, і температура, і склад крові, і показники кардіограм, тощо.
Транспортні об’єкти не такі складні, як біологічні системи, тому для характеристики їх стану існує значно менше параметрів. Наприклад, характеристикою стану технічного об’єкта може бути його надійність, працездатність, ступінь зношення, амортизація, тощо. Але це технічні питання, які відносяться до компетенції механіків, енергетиків, спеціалістів вагонного господарства, зв’язку і т.д. Спеціалістів з управління процесами перевезень цікавлять такі характеристик системи, які дають можливість визначати показники функціонування. Такими характеристиками для різних об’єктів можуть бути: кількість поїздів на станції чи у окремому парку, кількість вагонів на окремій колії чи у парку, кількість вантажу на складі, кількість контейнерів на площадці, кількість пасажирів біля квиткової каси чи на вокзалі і т.д.
Отже, ознакою функціонування системи є зміна з часом параметрів стану системи, а у залежності від того яким чином і коли система змінює свій стан, розрізняють і характер процесу. Якщо стан системи (наприклад, кількість поїздів у парку) змінюється з часом, але таким чином, що можна розрахувати характеристику стану системи у будь-який момент часу – говорять, що в системі відбувається детермінований процес. Чи може таке бути і за яких умов?
Для відповіді на це питання давайте розглянемо процес функціонування приймально-відправного парку станції, наведеного у графічному вигляді на рис. 6.1.
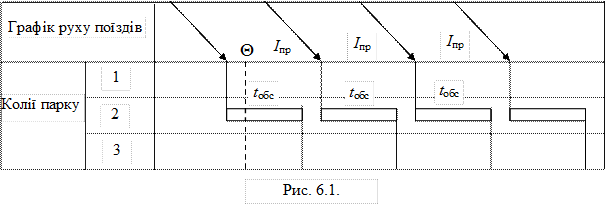
На цьому графіку видно, що процес функціонування має циклічний характер, стан системи змінюється в окремі моменти часу, а саме: в момент прибуття поїзда і в момент закінчення його обробки (відправлення). Знаючи параметри Іпр, tобс і стан системи в момент часу Θ, є можливість розрахувати стан системи у будь-який момент Т. Такий процес називається детермінований, і може протікати тільки за умов регулярного вхідного потоку і постійної тривалості обслуговування.
Коли вхідний потік до системи має випадковий характер, або тривалість обслуговування є випадковою величиною (або обидва разом) – стан системи змінюється випадковим чином (рис. 6.2), отже в системі відбувається випадковий процес.

Характеристикою стану такої системи можна вважати кількість поїздів (n), яка знаходиться у парку в довільний момент часу. Розглядаючи приклад на рис. 6.2, можна відзначити, що в окремі періоди у парку знаходиться n=0, 1, 2 поїзда, а зміна стану системи відбувається у довільні моменти часу, а саме: в моменти прибуття чергового поїзда і в моменти закінчення обробки (відправлення) чергового поїзда. В умовах випадкового вхідного потоку і випадкової тривалості обслуговування ці моменти також мають випадковий характер, тобто зміна стану системи відбувається у випадкові моменти часу, а це ознака випадкового процесу.
Для таких процесів стан системи є величина випадкова і змінюється у випадкові моменти часу. Для математичного опису випадкових величин використовують ймовірність (Р) їх здіснення. Зміст ймовірності стану можна пояснити як частку часу знаходження системи у відповідному стані. Наприклад, якщо на графіку функціонування системи (рис. 6.2) виділити відрізки часу (tn)з постійною кількістю поїздів в системі (n), тоді за деякий розрахунковий період (Т) частку часу знаходження системи в окремому стані можна визначити як
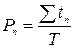 .
.
Зрозуміло, що це лише пояснення змісту ймовірності стану, і ніхто їх так не визначає, а розраховують з допомогою теоретичних формул у залежності від типу процесу. Математичний опис Pn залежить від того, як і в які моменти часу система може змінювати свій стан. За цими ознаками серед безлічі можливих випадків окремо виділяють марковські процеси – такі випадкові процеси, які володіють властивістю „відсутності післядії”, яка полягає у наступному. „Для кожного моменту часу Θ ймовірність будь-якого стану системи у майбутньому (T > Θ) залежить тільки від стану у даний момент (Θ) і не залежить від того, коли і яким чином система прийшла у цей стан”. Іншими словами, для Маяковського процесу його майбутній розвиток залежить тільки від стану у даний момент і не залежить від історії процесу. А це може бути тільки у випадку, коли вхідний потік і тривалість обслуговування також володіють цією властивістю, тобто у випадку найпростішого вхідного потоку (υвх= 1) і тривалості обслуговування, що розподілена за показниковим законом (υобс= 1). Для інших випадків сучасна наука не здатна отримати математичний опис Pn.
6.2. Визначення ймовірностей станів систем з марковським процесом.
Зробити математичний опис випадкового процесу – це значить отримати формулу для визначення ймовірності будь-якого стану системи у довільний момент часу Pn = f(T). Розглянемо методику отримання такого опису для марковського процесу з дискретними станами (n = 0, 1, 2 ..) і неперервним часом. Випадковий процес, елемент якого розглянуто на рис. 6.2 можна подати у вигляді функціональної схеми (рис. 6.3), на якій перелічені усі можливі стани системи (показано квадратами) і можливі переходи системи зі стану в стан (показано стрілочками) за елементарний проміжок часу (Δt→0).
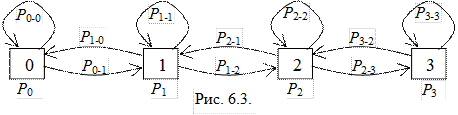
Розглянемо зміст цієї схеми. Чому приведено тільки 4 можливих стани системи? Згідно з графіком на рис. 6.1 парк станції має три колії, отже можливі його стани наступні: відсутні поїзда у парку – стан 0 (n=0); у парку знаходиться 1 поїзд – стан 1 (n=1); у парку знаходиться 2 поїзда – стан 2 (n=2); у парку знаходиться 3 поїзда – стан 3 (n=3). Інші стани при трьох коліях у парку неможливі (якщо не приймати до уваги ті поїзда, що можуть знаходитись перед парком у стані очікування прийому у зв’язку із заняттям усіх колій). Таким чином, на графі станів наведені усі можливі стани парку, які показані квадратами. Дугами зі стрілочками показані можливі переходи системи зі стану в стан і відповідно підписані Рi-j, що означає ймовірність переходу системи зі стану і в стан j.
Може виникнути запитання, а чому не розглядаються переходи системи зі стану 1 в стан 3, чи зі стану 2 в стан 0? Пояснення полягає у тому, що розглядається марковський процес з найпростішим вхідним потоком, отже за елементарний проміжок часу (Δt→0) згідно з властивістю ординарності не м
– Конец работы –
Эта тема принадлежит разделу:
В передбачити точний результат процесу дуже важко, або навіть неможливо
Поняття системи... Явища що мають місце у природі дуже різноманітні і так пов язані між собою... Відомий вираз так званого ефекту метелика Якщо метелик змахне крильцями над Карибським морем це може призвести до...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Приклади.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов