Задача №4. Напряжения в грунтах от действия внешних сил
Исходные данные:
К горизонтальной поверхности массива грунта приложена вертикальная неравномерная нагрузка, распределенная в пределах гибкой полосы (ширина полосы b = 500 см) по закону трапеции от P1 = 0,26 МПа до P2 = 0,36 МПа. Определить величины вертикальных составляющих напряжений σZ в точках массива грунта для заданной вертикали, проходящей через точку М4 загруженной полосы, и горизонтали, расположенной на расстоянии Z = 200 см от поверхности. Точки по вертикали расположить от поверхности на расстоянии 100, 200, 400, 600 см. Точки по горизонтали расположить вправо и влево от середины загруженной полосы на расстоянии 0, 100, 300 см. По вычисленным напряжениям построить эпюры распределения напряжений σZ.
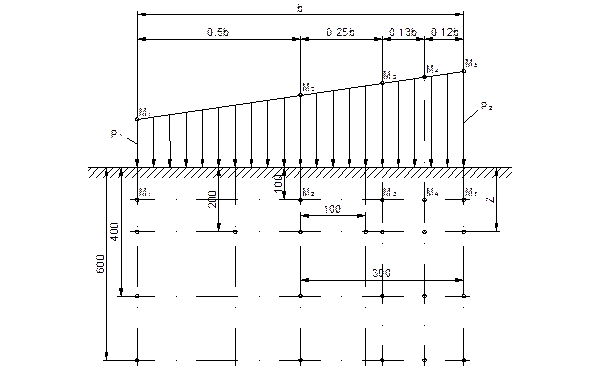
Рис. 4-1. Расчетная схема
Решение:
Для случая действия на поверхности массива грунта нагрузки, распределенной в пределах гибкой полосы по трапецеидальной эпюре, величину вертикальных сжимающих напряжений в заданной точке массива грунта определяют путем суммирования напряжений от прямоугольного и треугольного элементов эпюры внешней нагрузки.
Вертикальные напряжения σZ, возникающие от действия полосообразной равномерно распределенной нагрузки (прямоугольный элемент эпюры внешней нагрузки) определяют по формуле:
 ,
,
где KZ – коэффициент, определяемый в зависимости от величины относительных координат;
P – вертикальная нагрузка.
Вертикальные напряжения σZ, возникающие от действия полосообразной неравномерной нагрузки, распределенной по закону треугольника (треугольный элемент эпюры внешней нагрузки), определяются по формуле:
 ,
,
где  – коэффициент, определяемый в зависимости от величины относительных координат;
– коэффициент, определяемый в зависимости от величины относительных координат;
P – наибольшая ордината треугольной нагрузки.
1. Рассмотрим вертикаль М4.
Слева трапеция длиной 440 см с крайними сторонами 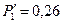 МПа и
МПа и 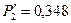 МПа, справа длиной 60 см с крайними сторонами
МПа, справа длиной 60 см с крайними сторонами  МПа и
МПа и  МПа. Разобьем левую трапецию на прямоугольник с боковой стороной
МПа. Разобьем левую трапецию на прямоугольник с боковой стороной 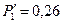 МПа и треугольник с боковой стороной
МПа и треугольник с боковой стороной  МПа, а правую трапецию на прямоугольник с боковой стороной
МПа, а правую трапецию на прямоугольник с боковой стороной  МПа и треугольник с боковой стороной
МПа и треугольник с боковой стороной  МПа.
МПа.

Для глубины 100 см:
 МПа
МПа
Для глубины 200 см:
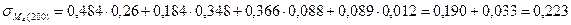 МПа
МПа
Для глубины 400 см:
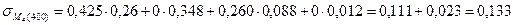 МПа
МПа
Для глубины 600 см:
 МПа
МПа
2. Рассмотрим горизонталь 200.
Пять точек {-300, -100, 0, 100, 300}, причем крайние точки находятся за пределами нагруженной поверхности.
а) Найдем величину вертикальных сжимающих напряжений в самой левой точке рассматриваемой горизонтали, то есть {-300}. Для этого продолжим трапецеидальную нагрузку до линии, проходящей через данную точку перпендикулярно поверхности. Получим две трапеции: одну длиной 550 см с меньшей боковой стороной равной 0,25 МПа, и большей боковой стороной равной 0,36 МПа; вторую – длиной 50 см с меньшей боковой стороной равной 0,25 МПа, и большей боковой стороной равной 0,26 МПа.
Искомая нагрузка будет равна разности нагрузок большой и малой трапеций.
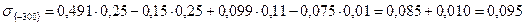 МПа
МПа
б) Найдем величину вертикальных сжимающих напряжений в точке рассматриваемой горизонтали {-100}. Для этого разделим трапецеидальную нагрузку в линии, проходящей через данную точку перпендикулярно поверхности. Получим две трапеции: слева длиной 150 см с меньшей боковой стороной равной 0,26 МПа, и большей боковой стороной равной 0,29 МПа; справа – длиной 350 см с меньшей боковой стороной равной 0,29 МПа, и большей боковой стороной равной 0,36 МПа.
Искомая нагрузка будет равна сумме нагрузок левой и правой трапеций.
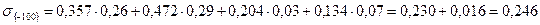 МПа
МПа
в) Найдем величину вертикальных сжимающих напряжений в точке рассматриваемой горизонтали {0}. Для этого разделим трапецеидальную нагрузку в линии, проходящей через данную точку перпендикулярно поверхности. Получим две трапеции длиной по 250 см каждая: слева с меньшей боковой стороной равной 0,26 МПа, и большей боковой стороной равной 0,31 МПа; справа – с меньшей боковой стороной равной 0,31 МПа, и большей боковой стороной равной 0,36 МПа.
Искомая нагрузка будет равна сумме нагрузок левой и правой трапеций.
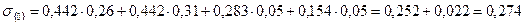 МПа
МПа
г) Найдем величину вертикальных сжимающих напряжений в точке рассматриваемой горизонтали {100}. Для этого разделим трапецеидальную нагрузку в линии, проходящей через данную точку перпендикулярно поверхности. Получим две трапеции: слева длиной 350 см с меньшей боковой стороной равной 0,26 МПа, и большей боковой стороной равной 0,33 МПа; справа – длиной 150 см с меньшей боковой стороной равной 0,33 МПа, и большей боковой стороной равной 0,36 МПа.
Искомая нагрузка будет равна сумме нагрузок левой и правой трапеций.
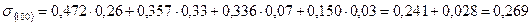 МПа
МПа
д) Найдем величину вертикальных сжимающих напряжений в самой правой точке рассматриваемой горизонтали, то есть {300}. Для этого продолжим трапецеидальную нагрузку до линии, проходящей через данную точку перпендикулярно поверхности. Получим две трапеции: одну длиной 550 см с меньшей боковой стороной равной 0,26 МПа, и большей боковой стороной равной 0,37 МПа; вторую – длиной 50 см с меньшей боковой стороной равной 0,36 МПа, и большей боковой стороной равной 0,37 МПа.
Искомая нагрузка будет равна разности нагрузок большой и малой трапеций.
 МПа
МПа
3. На основании проведенных расчетов строим эпюры распределения σZ.

Рис. 4-2. Эпюры напряжений σZ от прямоугольной составляющей внешней нагрузки
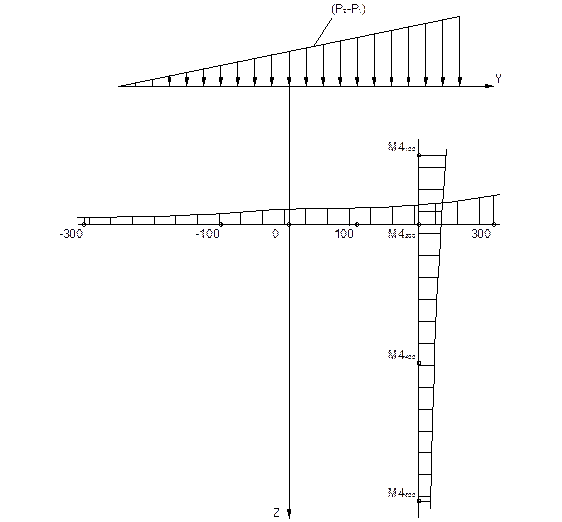
Рис. 4-3. Эпюры напряжений σZ от треугольной составляющей внешней нагрузки

Рис. 4-4. Суммарные эпюры напряжений σZ