Цилиндр вращения.
Если ось вращения перпендикулярна П1, то на эту плоскость цилиндр будет проецироваться в виде окружности, а на две другие плоскости проекций в виде прямоугольников, ширина которых равна диаметру этой окружности. Такой цилиндр является проецирующим к П1.
Если ось вращения перпендикулярна П2, то на П2 он будет проецироваться в виде окружности, а на П1 и П3 в виде прямоугольников.
Аналогичное рассуждение при положении оси вращения, перпендикулярном П3 (рис.8.3).

Рис.8.3
Цилиндр Ф пересекается с плоскостями Р ,S ,L и Г (рис.8.3).
2 ГПЗ, 1 алгоритм (Модуль №3)
Ф ^ П3
Р, S, L, Г ^ П2
Ф Ç Р = а (6 5 и 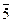
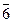 )
)

Ф ^ П3 Þ Ф3 = а3 (63 =53 и 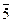 =
=  )
)
а2 и а1 строятся по принадлежности к поверхности Ф.
 Ф Ç S = b (5 4 3
Ф Ç S = b (5 4 3 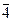
 )
)
Ф Ç S = с (2 3  ) Рассуждения аналогичны предыдущему.
) Рассуждения аналогичны предыдущему.
Ф Г = d (12 и 
Задачи на рисунках 8.4, 8.5, 8.6 решаются аналогично задаче на рис.8.3, так как цилиндр
везде профильно-проецирующий, а отверстия - поверхности проецирующие относительно
П1 - 2ГПЗ, 1 алгоритм (Модуль №3).
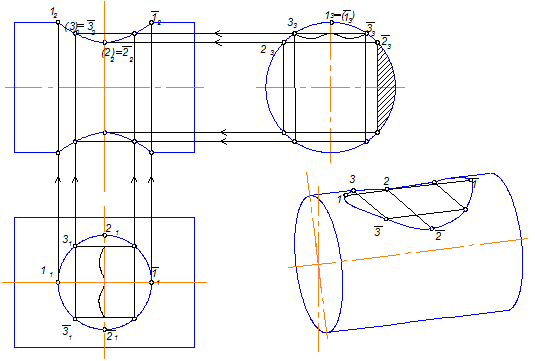
Рис. 8.4

Рис. 8.5

Рис. 8.6
Если оба цилиндра имеют одинаковые диаметры (рис.8.7), то линиями пересечения их будут два эллипса (теорема Монжа, модуль №3). Если оси вращения этих цилиндров лежат в плоскости, параллельной одной из плоскостей проекций, то на эту плоскость эллипсы будут проецироваться в виде пересекающихся отрезков прямых.
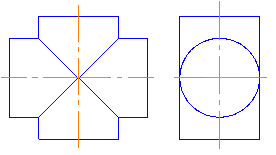
Рис. 8.7