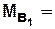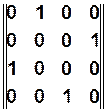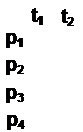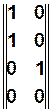Моделирование и оценивание характеристик сложных систем
II. Моделирование и оценивание характеристик сложных систем
Теоретико-множественное описание сложных систем
2.1. Понятие множества
Определение 2.1. Множеством называется объединение в одно целое некоторой совокупности объектов хорошо различимых нашей интуицией или мыслью.
Множество — это первичное понятие. Поэтому определять его через другие понятия затруднительно. Множества обычно обозначаются большими латинскими буквами.
А, В, С или X, Y, Z
Элементы множества обозначают малыми буквами
А, в, с или x, y, z
xÎX (xÏX). В теории четких (классических) множеств может быть только две альтернативы: … xÎXлибо (xÏX).Примеры теоретико-множественного описания сложных систем
3.1. Сетевые модели сложных систем (СМСС).
СМСС задаются следующим образом
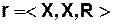
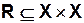
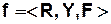
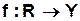
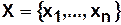
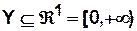
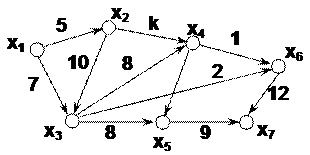 Пример.
Пример.
3.2. Динамические модели сложных систем
Определение 3.1. Статическая модель описывает связь между компонентами состояний или между этими компонентами и другими характеристиками системы в условиях равновесия и других условиях «замораживания» изменения состояния.
Определение 3.2. Динамической называется модель, в которой в той или иной форме раскрываются причинно-следственные связи (реализуется принцип причинности), определяющие развивающийся во времени процесс перехода системы из одного состояния в другое.
Принцип причинности предполагает выполнение следующих условий:
a) упорядоченность причинно-следственных связей во времени. Это означает, что состояние и выходная ситуация (выход) системы в любой момент времени не зависит от ситуаций, которые могут возникнуть на входном полюсе системы в более поздние моменты времени.
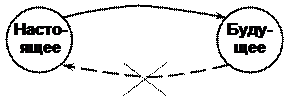
b) однозначность причинно-следственных связей. Это означает, что состояние и выходная ситуация (выход) системы в любой момент времени в будущем может быть определена совершенно точно (однозначно), если точно известны:
o все сведения о системе, характеризующие ее, и воздействие на нее среды в прошлом и настоящем;
o входное воздействие на систему в будущем.
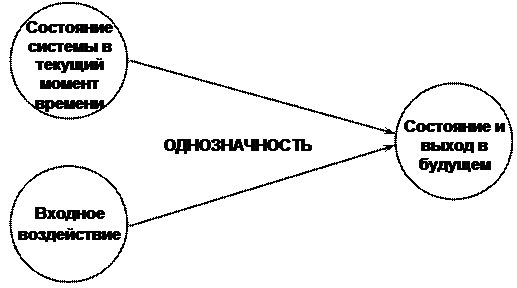
Первая часть этого принципа (пункт а) эквивалента утверждению о том, что будущее системы не влияет на прошлое и констатирует необратимость явлений во времени. Вторая часть данного принципа (пункт b) отражает принципиальную познаваемость причинно-следственных связей в системе и возможность точного предсказания выхода системы при наличии необходимой информации.
Таким образом, система, удовлетворяющая принципу причинности, является динамической системой.
Определение 3.3. Кинематической моделью называется модель динамической системы, описывающая изменение состояния как функции времени и не раскрывающая причинно-следственные связи, вызывающие это изменение.
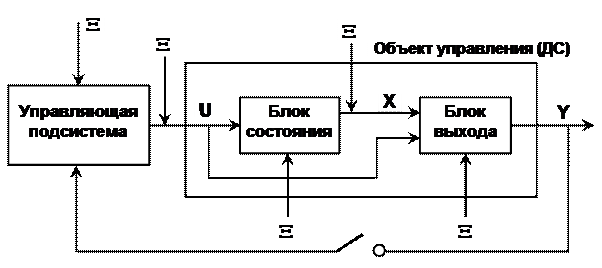
Динамическая система (ДС) задается с использованием 4-х основных (базисных) множеств: 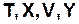 и 2-х отображений:
и 2-х отображений: 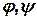 . При этом
. При этом
 — множество состояний ДС,
— множество состояний ДС,
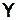 — множество выходов ДС,
— множество выходов ДС,
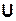 — множество управляющих воздействий,
— множество управляющих воздействий,
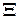 — множество возмущающих воздействий,
— множество возмущающих воздействий,
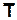 — множество моментов времени,
— множество моментов времени,
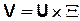 — множество входных воздействий,
— множество входных воздействий,
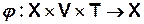 — переходное отображение, (1)
— переходное отображение, (1)
 — выходное отображение, (2)
— выходное отображение, (2)
Переходное и выходное отображения задаются как функции
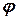 и
и 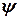 .
.
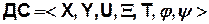 — классическая ДС.
— классическая ДС.
При этом каждое из множеств 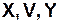 может быть в свою очередь конечным, счетным, континуальным, превышающим мощность континуума; множество
может быть в свою очередь конечным, счетным, континуальным, превышающим мощность континуума; множество 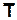 может быть континуальным и дискретным (счетным либо конечным).
может быть континуальным и дискретным (счетным либо конечным).
Обобщенное описание ДС позволяет, анализируя свойства множеств и отображений:
- образовывать различные конкретные частные классы моделей ДС;
- устанавливать взаимосвязи между указанными классами;
- организовывать многомодельные исследования реально протекающих процессов.
Основные классы задач теории управления ДС (ТУ ДС) (детерминированный вариант задания исходных данных)
| Элементы ДС Классы задач ТУ ДС | U | X | Y |
| Задачи анализа | + | + | ? |
| Задачи наблюдения (мониторинга) | + | ? | + |
| Задачи управления | ? | + | + |
Пример.Конечномерные дифференциальные динамические системы (КДДС).
 ,
, 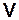 ,
, 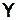 — представляет собой конечномерные пространства,
— представляет собой конечномерные пространства, 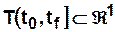
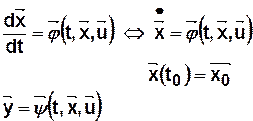
Нестационарная линейная ДДС (НЛДДС)

Стационарная линейная ДДС (СЛДДС)

Билинейная КДДС
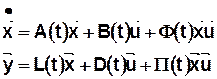
Рассмотрим частный случай ДС — конечные автоматы (КА) (конечные ДС).
В общем случае КА задаются на 3-х основных множествах с использованием 2-х отображений вида:
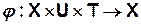 (3)
(3)
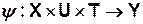 (4)
(4)
Будем рассматривать детерминированные КА (возмущающее воздействие отсутствует 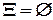 ). Тогда
). Тогда
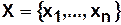 ,
, 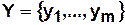 ,
, 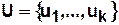 — конечные множества.
— конечные множества.
Функционирование КА интерпретируется как переходы КА из состояния в состояние, которые происходят в дискретные моменты времени (такты) 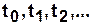 , имеющие нумерацию
, имеющие нумерацию 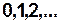 . В этом случае, базисное множество
. В этом случае, базисное множество 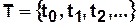 представляется в виде счетного множества вида
представляется в виде счетного множества вида 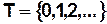 .
.
КА является ДС со счетным множеством моментов времени и относится к классу ДС с дискретным временем. Если интервалы между последовательными тактами равны, говорят о синхронной конечной ДС, в противном случае об асинхронной.
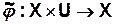 (5)
(5)
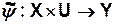 (6)
(6)
Из анализа выражений (2.9.5) следует, что переходная функция 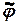 сопоставляет каждой паре символов
сопоставляет каждой паре символов 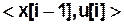 (<состояние предыдущего такта, текущий вход>) символ текущего состояния
(<состояние предыдущего такта, текущий вход>) символ текущего состояния
автомат 1 рода 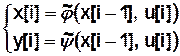 — несдвинутая выходная ф-ция
— несдвинутая выходная ф-ция
автомат 2 рода 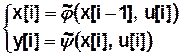 — сдвинутая выходная ф-ция
— сдвинутая выходная ф-ция
Возможен вариант задания автомата, когда выходная функция имеет вид:
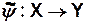
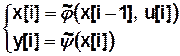 — автомат типа «вход–выход» или автомат Мура
— автомат типа «вход–выход» или автомат Мура
2-го рода.
Иногда при определении автомата рассматривают не пятерку 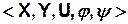 , а шестерку
, а шестерку 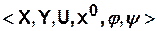 , где
, где 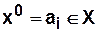 — начальное состояние автомата.
— начальное состояние автомата.
Наиболее часто встречаются 5 основных способа задания КА:
- задание КА табличный способ задания КА,
- задание КА с помощью орпсевдографов,
- задание КА с помощью специальных булевых матриц,
- задание КА с помощью специальных грамматик,
- задание КА с помощью рекуррентных отношений.
Пример. Рассмотрим конечный автомат (КА) Мура.
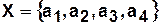 ,
, 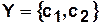 ,
, 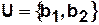
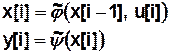
а) Табличный способ задания КА.
| Вход Состояние | 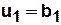
| 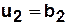
|
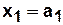
| 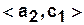
| 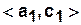
|
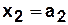
| 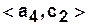
| 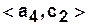
|
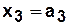
| 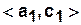
| 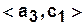
|
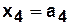
| 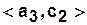
| 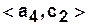
|
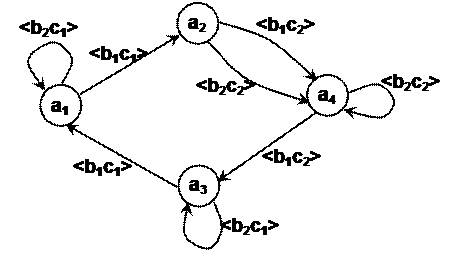
б) Графический способ задания КА. Орпсевдограф (допускается наличие петель в вершинах графа и множественность ребер).
в) Матричный вариант задания КА (используются специальные булевые матрицы).
Число строк и столбцов матрицы соответствует количеству состояний КА.
| 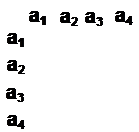
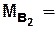 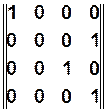
| 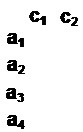
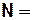 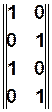
|
Состоянию 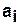 отвечает вектор-строка
отвечает вектор-строка 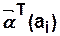 , в которой все элементы нулевые, кроме элемента, соответствующего
, в которой все элементы нулевые, кроме элемента, соответствующего 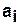 и принимающего значение равное единице.
и принимающего значение равное единице.
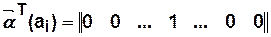
Например, 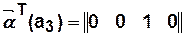
Выходному элементу 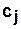 соответствует булева вектор-строка вида:
соответствует булева вектор-строка вида:
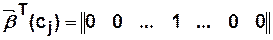
Введенное представление позволяет рассчитать матричными методами выход КА при любом начальном состоянии и любой последовательности входных воздействий.
Пример.
Дано 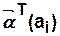 — начальное состояние КА,
— начальное состояние КА,
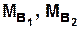 — сценарий задания входного воздействие (2 такта).
— сценарий задания входного воздействие (2 такта).
Найти 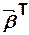 .
.
Переходное состояние автомата определяется по формуле 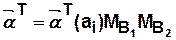
Тогда выход автомата определится по следующей формуле
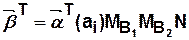
3.3. Сети Петри — причинно-следственные динамические модели параллельных действий.
Определение 3.4. Ординарной маркированной сетью Петри называется пятерка следующего вида
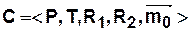
где 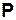 — конечное множество позиций
— конечное множество позиций 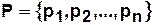 ,
,
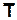 — конечное множество переходов
— конечное множество переходов 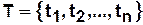 ,
,
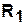 и
и 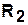 — графики бинарных отношений, заданных на множествах
— графики бинарных отношений, заданных на множествах 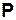 и
и 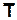 :
: 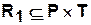 и
и 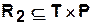 .
.
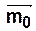 — вектор начальной маркировки
— вектор начальной маркировки 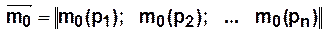 ,
, 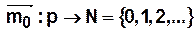 .
.
Геометрически сеть Петри задается двудольным графом, который конструктивно задается с помощью двух бинарных отношений 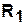 и
и 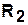 :
:
1. 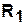 задает связь входных позиций с переходом,
задает связь входных позиций с переходом,
2. 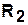 задает связь выходных позиций с переходом.
задает связь выходных позиций с переходом.
Маркер (фишка) геометрически задается как 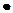 и располагается в заданной позиции.
и располагается в заданной позиции.
Существуют взаимно однозначные соответствия между графиками отношений 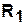 и
и 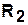 и представлением структуры сети Петри с помощью входной и выходной функций инцидентности
и представлением структуры сети Петри с помощью входной и выходной функций инцидентности 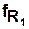 и
и 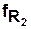 :
:
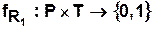 ,
, 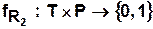
Данные функции, в свою очередь, описываются матрицами инцидентности 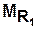 и
и 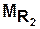 рассматриваемых отношений и графа.
рассматриваемых отношений и графа.
Пример. Пусть с помощью сети Петри мы описываем процесс функционирования вычислительной системы (ВС). Тогда структура ВС задается с помощью 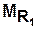 и
и 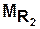 :
:
|
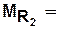 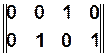
|
Нахождение маркера в соответствующей позиции сети Петри интерпретируется следующим образом:
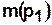 — задание находится в состоянии ожидания,
— задание находится в состоянии ожидания,
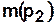 — процессор находится в состоянии ожидания,
— процессор находится в состоянии ожидания,
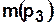 — задание выполняется процессором,
— задание выполняется процессором,
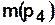 — задание выполнено и ожидает вывода,
— задание выполнено и ожидает вывода,
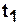 — начало выполнения задания,
— начало выполнения задания,
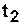 — конец выполнения задания.
— конец выполнения задания.
Определение 3.5. Маркированной сетью Петри общего вида называется пятерка следующего вида
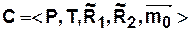
где 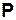 — конечное множество позиций,
— конечное множество позиций,
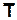 — конечное множество переходов
— конечное множество переходов
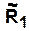 и
и 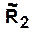 — графики бинарных отношений, заданных на множестве
— графики бинарных отношений, заданных на множестве 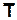 и мультимножестве
и мультимножестве 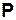 с неограниченных тиражированием.
с неограниченных тиражированием.
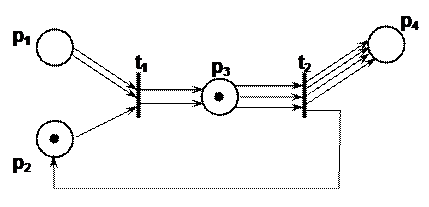
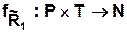 ,
, 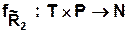
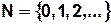
Принципы функционирования сети Петри
В основе функционирования сети Петри лежит процесс изменения ее маркировки (переход из одного состояния в другое). В случае запуска (срабатывания) соответствующих переходов, конструктивно правило функционирования сети Петри задается с помощью:
- правил разрешения переходов,
- правил изменения состояний маркировки при запуске (срабатывании) перехода.
Правило разрешения перехода.
Переход 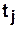 разрешен, если каждый его входной дуге (ребру)
разрешен, если каждый его входной дуге (ребру) 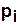 может быть поставлен в соответствие по крайней мере один маркер (фишка) в позиции, из которой данная дуга исходит. Это правило может быть записано следующим образом
может быть поставлен в соответствие по крайней мере один маркер (фишка) в позиции, из которой данная дуга исходит. Это правило может быть записано следующим образом
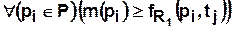 .
.
Существует эквивалентная запись в векторно-матричной форме
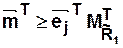 .
.
где 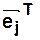 — вектор-строка, которая имеет число элементов, равное числу переходов, из них
— вектор-строка, которая имеет число элементов, равное числу переходов, из них 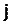 –й равен 1, а остальные — нулевые.
–й равен 1, а остальные — нулевые.
Правило изменения состояния маркировки.
При запуске перехода 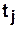 из каждой его входной позиции
из каждой его входной позиции 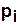 должно быть изъято число маркеров (фишек) равное кратности ребер, соединяющих позицию
должно быть изъято число маркеров (фишек) равное кратности ребер, соединяющих позицию 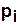 и переход
и переход 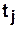 , и в каждую его выходную позицию
, и в каждую его выходную позицию 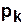 должно быть дополнительно помещено к уже имеющимся маркерам число маркеров (фишек) равное кратности ребер, соединяющих переход
должно быть дополнительно помещено к уже имеющимся маркерам число маркеров (фишек) равное кратности ребер, соединяющих переход 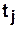 с позицией
с позицией 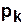 .
.
Данное правило записывается в эквивалентной векторно-матричной форме следующим образом:
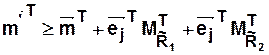
Пример

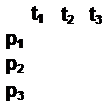 | 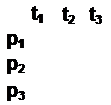 |
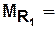
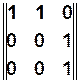 ,
, 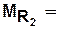
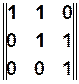 ,
, 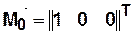
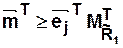
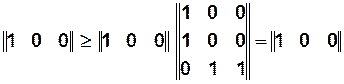 — переход
— переход 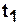 может сработать.
может сработать.
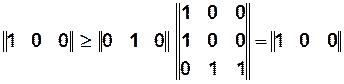 — переход
— переход 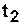 может сработать.
может сработать.
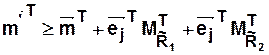
Пусть сработал переход  .
.
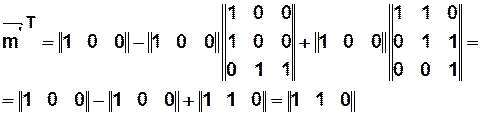
Пусть сработал переход 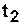 .
.
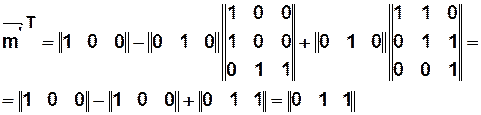
Построение деревьев достижимости
Основные методы анализа сети Петри базируются на построении и исследовании деревьев достижимости для соответствующих сетей Петри. Суть процедуры построения состоит в следующем. В качестве корня дерева принимается вершина графа, соответствующая начальной маркировке сети Петри. Далее выявляются все разрешенные при этой маркировке переходы и определяются получаемые при их запуске маркировки, каждой из которых сопоставляется вершина дерева, непосредственно достижимая из начальной. Затем та же процедура повторяется для каждой из этих вершин и т.д.
Тупиковые вершины — это вершины, из которых уже нельзя осуществлять никакие переходы.
Дублирующие вершины — это вершины, в которых повторяется маркировка.
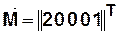 — корневая или начальная вершина.
— корневая или начальная вершина.
 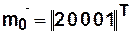
| |||||
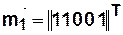
| 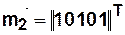
| ||||
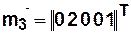
| 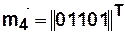
| 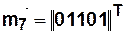
| 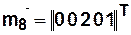
| ||
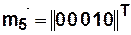
| 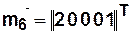
| ||||
Основы структурного анализа сложных объектов и систем.
Определение 4.1. Структурный анализ — научное направление, имеющее своей целью исследование таких основных характеристик структур сложных систем,… Ориентированный маршрут (ормаршрут) — это такая последовательность ребер (дуг)… Путь — ормаршрут, в котором нет повторяющихся дуг и отсутствует совпадение начальной и конечной вершин.Пример.
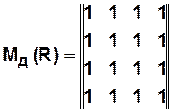 ,
, 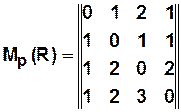
4.2. Показатели (характеристики) количественного оценивающие структуры сложных систем (СлС).
4.2.1. Показатель связности структуры СлС.
Показатель связности структуры 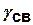 для
для 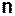 –вершинного графа определяется как отношение суммарного числа ребер к минимальному их числу, при котором может быть построен связный граф с
–вершинного графа определяется как отношение суммарного числа ребер к минимальному их числу, при котором может быть построен связный граф с 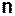 вершинами (величина
вершинами (величина 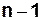 ). Для ориентированного графа показатель связности
). Для ориентированного графа показатель связности 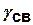 может быть определен как отношение суммы полустепеней исхода (или захода) вершин, равной сумме элементов матрицы смежности
может быть определен как отношение суммы полустепеней исхода (или захода) вершин, равной сумме элементов матрицы смежности 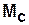 к величине
к величине 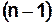 .
.
Показатель связности для ориентированного графа:

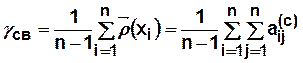
Показатель связности для неориентированного графа:
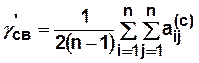
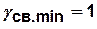
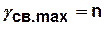
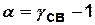 — показатель избыточности.
— показатель избыточности.
Пример. Для приведенного на рис. 4.4 графа (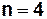 ) показатель связности
) показатель связности 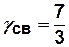 , а показатель избыточности
, а показатель избыточности 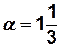 .
.
4.2.2. Показатель достижимости структуры СлС.
Коэффициент достижимости 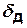 определяется для ориентированных графов как отношение суммы всех элементов матрицы достижимости
определяется для ориентированных графов как отношение суммы всех элементов матрицы достижимости 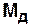 к
к 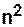 :
:
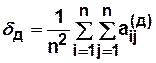
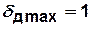
Пример. Для графа, изображенного на рис.4.4, 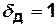 . Если на этом графе удалить вершину
. Если на этом графе удалить вершину 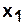 , то имеем следующую структуру:
, то имеем следующую структуру:
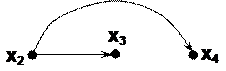
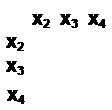 В этом случае получаем матрицу достижимости следующего вида
В этом случае получаем матрицу достижимости следующего вида
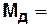
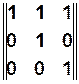 и имеем
и имеем 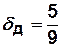 .
.
4.2.3. Показатели компактности структуры СлС.
Данные показатели определяются на основе матрицы расстояний 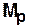 .
.
Эксцентриситеты вершины графа 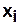 — это наибольшее из кратчайших расстояний от вершины
— это наибольшее из кратчайших расстояний от вершины 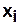 до других вершин графа
до других вершин графа 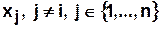 . Для каждой вершины графа
. Для каждой вершины графа 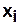 эксцентриситет равен
эксцентриситет равен
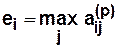
Радиус 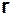 — наименьший из эксцентриситетов графа
— наименьший из эксцентриситетов графа
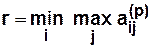
Диаметр  — наибольший из эксцентриситетов графа
— наибольший из эксцентриситетов графа
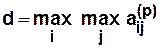
Центральная вершина графа — это та его вершина 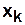 , для которой выполняется следующее условие
, для которой выполняется следующее условие
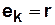
Центр графа — множество центральных вершин.
Чем 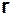 и
и  меньше, тем структура компактнее.
меньше, тем структура компактнее.
Пример. Из матрицы расстояний 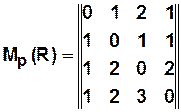 получаем
получаем 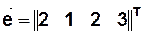 ,
, 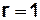 ,
, 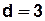 . Центр состоит только из одной центральной вершины
. Центр состоит только из одной центральной вершины 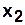 .
.
Интегральный показатель структурной компактности определяется как сумма всех элементов матрицы расстояний 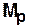 (чем меньше этот показатель, тем структура компактнее)
(чем меньше этот показатель, тем структура компактнее)
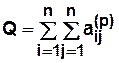
Для полного графа 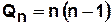 .
.
Относительный показатель компактности
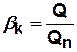
Пример. Для графа рис. 4.4 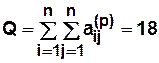 ,
, 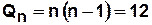 ,
, 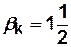
4.2.4. Показатель централизованности структуры СлС.
Данный показатель определяется следующим образом: для каждой вершины матрицы смежности 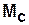 подсчитывается суммарное число входящих и выходящих дуг (полустепеней захода и исхода)
подсчитывается суммарное число входящих и выходящих дуг (полустепеней захода и исхода)
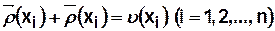
Находят наибольшее из них 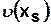 ,определяют разность между
,определяют разность между 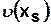 и
и 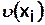 и суммируют эти разности. Максимально возможное значение этой суммы будет
и суммируют эти разности. Максимально возможное значение этой суммы будет 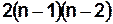 . Тогда индекс централизованности определится следующим соотношением:
. Тогда индекс централизованности определится следующим соотношением:
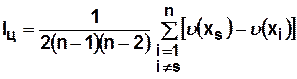 .
.
Пример. Для рассматриваемого графа (рис. 4.4) 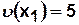 ,
, 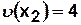 ,
, 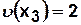 ,
, 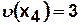 . Следовательно
. Следовательно 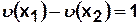 ,
, 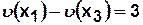 ,
, 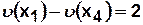 ,
, 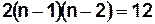 . Таким образом,
. Таким образом, 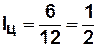 .
.
Примеры типовых структур современных
телекоммуникационных систем.
 Цепь
Цепь 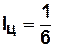
| 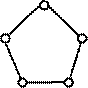 Круг
Круг 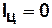
|
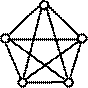 Полный граф
Полный граф 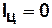
|  Штурвал
Штурвал 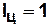
|
Выводы. Зная показатели (характеристики), оценивающие структуры СлС, мы можем при проектировании или эксплуатации соответствующих информационных систем говорить о тех или иных свойствах данных систем. Так, например,
- если система имеет высокую степень связности, большую избыточность и равномерные распределения связи, то она обладает высокой надежностью;
- если система имеет минимальный показатель компактности, то это обуславливает высокое быстродействие системы;
- если степень централизованности мала, то имеем распределенную структуру, обладающую высокой степенью живучести.