ЭНЕРГЕТИЧЕСКАЯ ТЕОРИЯ ПРОЧНОСТИ

Энергетическая теория основывается на предположе­нии о том, что количество удельной потенциальной энергии деформации, накопленной к моменту наступления предельного напряженного состо­яния в материале, одинаково как при любом слоокном напряженном состоянии, так и при простом растяжении.

При построении данной теории первоначально была предложена гипотеза, согласно которой за причину наступления предельного напря­женного состояния принималась полная удельная потенциальная энер­гия, достигающая своего наибольшего значения.

Условие, отвечающее такой гипотезе, записывается в следующем виде:

U<U₀, (12.11)

где U — полная удельная энергия, которую для общего случая объемного напряженного состояния определяют по извест­ной формуле *

^ ⁼ 2£~ f^ст» + °* + "*~ ^2f( (^CTl02 + ^ai°³ + ^а2⁰з)]; (a)

U_o — предельное значение энергии, определяемое из опыта на простое растяжение. Формула для ее вычисления легко получается, если в правой части (а) положить ст₂ = а₃ — 0 и вместо ctj подставить предельное напряжение при растя­жении, т. е. а₀. Таким образом,

tft-gf-. (б)

С учетом (а) и (б) условие (12.11) в развернутом виде запишется так:

У O'j + 05 + 0з - 2р (О^., + (TjOg -I- CJ₂CJ₃) < О₀. (В)

* См. гл. III, § 33, формула (3.50). 298

Указанная гипотеза, однако, не оправдалась на опыте и поэтому основанная на ней теория не нашла применения на практике.

Так, например, эта теория не подтверждается на опыте со всесто­ронним гидростатическим давлением, при котором, как уже говори­лось выше, разрушение практически не наступает.

Таким образом, энергия, соответствующая изменению объема вследствие всестороннего сжатия, не может служить критерием проч­ности.

В предложенной новой энергетической теории за исходную была принята гипотеза, согласно которой за причину наступления предель­ного напряженного состояния принимается не вся удельная энергия, а лишь та ее часть, которая накапливается вследствие изменения формы кубика с ребром, равньш единице.

Как видно, новая энергетическая теория связывается с развитием только пластических деформаций, которые, как известно, характери­зуются изменением формы тела, но не сопровождаются изменением его объема.

Условие, которое должно соблюдаться при применении данной теории, выражается неравенством

и_ф<и_фо, (12.12)

где 1/ф — расчетная величина энергии, связанной с изменением

формы кубика при исследуемом напряженном состоянии;

(/фо — предельное значение той же энергии, получаемое из опыта

на простое растяжение.

Для общего случая напряженного состояния непосредственное вычисление энергии, идущей на изменение формы, вызывает затрудне­ние. Поэтому величину (У_ф находят, пользуясь выражением

и = и_у±и_ф, (12.13)

откуда

U^U-U_V. (12.14)

Здесь U — полная энергия;

U _v — энергия, затрачиваемая на изменение объема.

В общем случае объемного напряженного состояния деформацию можно разделить на две: 1) деформацию, связанную только с изменением объема, и 2) деформацию, соответствующую только изменению формы.

Для этого представим заданное напряженное состояние (рис. 301, а), определяемое главными напряжениями а_и о₂, о₃, в виде суммы двух напряженных состояний (рис. 301, б, в). Пусть первое из них соответ­ствует гидростатическому растяжению (сжатию), при котором по всем граням кубика действуют одинаковые средние напряжения

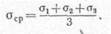
Так как в этом случае длины всех ребер кубика изменяются на одина­ковую величину, то форма кубика не меняется, а меняется только его объем.

299.

Напряжения второго напряженного состояния обозначим о[, а'_г и о'_я. Они будут определяться равенствами:

^1 = 01 —а_ср; а.2 = ст₂ —ст_ср; а'₃ = а₃ — а_ср. (д)

Легко показать, что изменение объема при напряжениях а[, о'% и а'_л равно нулю.

Действительно, подставив значения этих напряжений из равенств (д) в формулу объемной деформации (3.48) (см. § 32), с учетом (г) получим

 

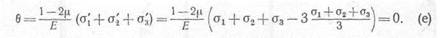
Поэтому от напряжений о, сь и о'₆ будет происходить только из­менение формы тела.

Для определения энергии U_v подставим в формулу (а) вместо a_lt On н а₃ напряжения <т_ср. Тогда

 

Вводя в выражение (ж) значение а_ср из равенства (г), получим

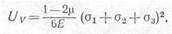
(з)

Подставляя теперь U и ^v из формул (а) и (з) в (12.14), после несложных преобразований найдем

(12.15)

Формула (12.15) легко приводится к виду

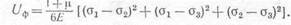
(12.16)

Для случая простого растяжения, когда сг₂ = о₃ = 0, согласно формуле (12.16) имеем

£/_#-i+J*2of. (12.17)

Условие (12.12) с учетом формул (12.16) и (12.17) запишется сле­дующим образом:

[{ах ~ ^)² + К - <т₃)² + («Ч - °з)² К 2а, (и)

где о₀ — предельное напряжение, найденное из опыта при простом растяжении.

В данной теории о₀ принимается равным пределу текучести о_т.

Расчетная формула, отвечающая условию (и), запишется в виде

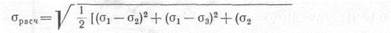
-a₃)²]=sS^, (12.18)

где R — расчетное сопротивление при растяжении.

При плоском напряженном состоянии, заменяя в формуле (12.18) соответствующие главные напряжения их выражениями через а_х, а_у и %_ix, получим