ЧИСТЫЙ ИЗГИБ КРИВОГО БРУСА

Для определения напряжений при чистом изгибе плоского кри­вого бруса, так же как для прямого бруса, считаем справедливой гипотезу плоских сечений. Определяя деформации волокон бруса, пренебрегаем напряжениями в радиальном направлении. Рассматри­ваем брусья с сечениями, симметричными относительно оси Оу, лежащей в плоскости кривизны бруса, и будем считать, что изгибающий мо­мент приложен в той же плоскости.

На рис. 344, а, б показан элемент бруса длиной ds с симметричным поперечным сечением. Ось Ох направим по нейтральной оси, вокруг которой поворачивается сечение.

Эпюра абсолютных удлинений волокон показана на рис. 344, в, а эпюра относительных удлинений изображена на рис. 344, г.

Абсолютное удлинение на высоте сечения изменяется по закону прямой линии, а относительное — по закону кривой линии (гипер­болы). Объясняется это тем, что значение длины дуги ds_p = р^ф также меняется по высоте и поэтому для произвольного волокна, отстоя­щего от нейтрального слоя на расстоянии у, имеем

Ads₉ Adq> у ЛЛр у ^р dsy dq> p dtp r--y'

Считая, что волокна друг на друга не давят, по закону Гука найдем

_п _ - А<% У

(14.1)

dtp г + у'

При чистом изгибе нормальная сила отсутствует, поэтому

Или с учетом (14.1) получим

 

но так как множитель, стоящий перед интегралом, не может рав­няться нулю, то

[-4-dF = 0. (14.2)

.3 г+у '

F

Равенство (14.2) является условием для определения положения нейтрального слоя. Из равенства видно, что нейтральная ось в кри-

 

вом брусе не проходит через центр тяжести, так как в последнем слу­чае должен был бы равняться нулю статический момент ^ydF, как это

F

было для прямого бруса (см. § 62).

Выразим теперь момент внутренних сил относительно нейтраль­ного слоя через напряжения и приравняем его внешнему моменту, взятому по абсолютной величине:

(14.3)

 

Интеграл, входящий в равенство (14.3), можно представить в виде

 

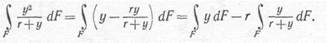
Второе слагаемое в полученном выражении согласно равенству (14.2) равно нулю, поэтому

 

где S_x = Fz/₀ — статический момент площади поперечного сечения относительно нейтральной оси (у₀ — расстояние от центра тяжести сечения до нейтральной оси).

Подстановка (14.4) в равенство (14.3) дает

Подставляя полученное выражение в формулу напряжений (14.1) и учитывая, что г + у = р, т. е. равно расстоянию от центра кри­визны до точки, в которой опре­деляется напряжение, окончательно получим

Формула и; существенно от­личается от формулы для прямого бруса прежде всего тем, что в знаменатель входит переменная вели­чина р, зависящая от у.

Эпюра напряжений в сечении кривого бруса изменяется по гипер­болическому закону (рис. 345). Наибольшие напряжения в сечениях, имеющих две оси симметрии, возникают в крайнем волокне, обра­щенном к центру кривизны. Знак напряжения, вычисленного по фор­муле (14.6), следует определять исходя из физического смысла.

Для того чтобы сравнить формулы для прямого и кривого бру­сьев, преобразуем формулу (14.6). Из (14.4) найдем

обозначим

Этот интеграл назовем моментом инерции для сечения кривого бруса. Значок вверху в виде дуги служит отличительным знаком от обычного осевого момента инерции. Легко заметить, что при г->- оо

/

момент инерции для кривого бруса в пределе совпадает с обычным осевым моментом инерции. Таким образом,

S_x = y7_x. . (14.7)

Подставляя это выражение в формулу (14.6) и учитывая, что р = г -- у, получим

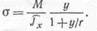
Если /■->- оо, то формула (14.8) в пределе совпадает с обычной фор­мулой для прямого бруса.

В § 114 дается сравнительная таблица результатов, получаемых по двум формулам: для кривого и прямого брусьев.