Do , С М , ■. п , .

di⁼*^±)irj^dz + ^C- <^а)

Это выражение определяет закон изменения углов поворота каса­тельной по длине балки.

После повторного интегрирования находим уравнение оси изо­гнутого бруса:

и = ± JJjg clzdz + Czi D. (б)

Для вычисления интегралов, входящих в выражения (а) и (б), необходимо сначала написать аналитические выражения изгибающего момента и жесткости. Постоянные интегрирования С и D находятся

из граничных условий, которые зависят от способов закрепления бруса.

Для уяснения сказанного рассмотрим примеры.

1. Составить выражение прогиба и угла поворота в произвольном сечении консольной балки, загруженной силой Р (рис. У

227). Рассматривая равно- ² ' '"

весне правой отсеченной части, найдем

М = — р (I - z).

Знак минус взят пото­му, что нижние волокна балки сжаты. Так как ось

О у направлена кверху, то в правой части дифференциального уравне­ния (9.5) надо взять знак плюс:

Для нашего случая имеем

d-v _ _Р(1-г)

d*> ~ ej ■

Предположим, что жесткость балки постоянна. Интегрируя один раз, получим

Интегрируя еще раз, имеем

Так как в заделке прогиб и угол поворота равны нулю, то для определения постоянных будем иметь следующие граничные условия:

при z = 0 ~=0;

при z = 0 V — 0.

Из уравнения (в) видно, что постоянная С представляет собой угол поворота в начале координат. Положив г = 0, находим С —' 0. Из уравнения (г) следует, что постоянная D — это прогиб в начале координат. Положив в уравнении (г) г = 0, получаем D — 0.

Итак, имеем:

-•_ _^£i I ^Рг:!.

" ~ ~ ~ШТ ^ ЩГТ^;

_ dv ___ Plz Pi*

У~~ dz~~~ EJ ⁺2£7⁴

 

Из рис. 227 видно, что наибольший прогиб будет под грузом. Поло­жив г — I, из первого уравнения найдем

Р1»

Угол поворота на конце балки

Р1* ¥'=—-2£7-

Знак минус у прогиба свидетельствует о том, что его направление не совпадает с положительным направлением оси у, минус в выраже­нии угла поворота показывает, что касательная не проходит в поло­жительной четверти осей координат.

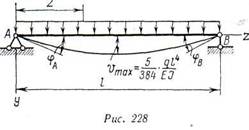
2. Определим прогибы двухопорной балки посто­янного сечения, показан­ной на рис. 228.

Так как ось у направле­на вниз, то в дифференци­альном уравнении необхо­димо взять знак минус: cPv _ М dz* ~" ~ EJ •

Изгибающий момент в произвольном сечении равен

Таким образом, дифференциальное уравнение запишется в следующем виде:

EJ _dz, = — ₂ <?^ + -₂ <7* • Последовательное интегрирование дает:

Е/Ф-£/£ — *? + £ +С; (д)

EJv = -*£ + -Ij + Cz + D. (e)

Для определения двух постоянных С п D необходимо иметь два условия. В рассматриваемом случае на левом и на правом концах прогиб равен нулю. Таким образом, граничные условия равны: при _г = 0 v — 0; при г = / v — 0.

Подставляя в уравнение (е) г — 0 и приравнивая прогиб нулю, получим DO; подставляя в это же уравнение г — I и также при­равняв прогиб нулю, имеем

-''''^"''-^cv-'o

12 ' 24 ' ^ь'-^и' 218

• Следовательно,