З - ei • а
Здесь v ■— прогиб в произвольном сечении первого участка;
М — функция,выражающая значение изгибающего момента
в произвольном сечении первого участка. Разложимфункцию прогиба щ в ряд Маклорена:
у, = vi (0) + v (0) 2 + в," (0) | + v{" (0) {' + .... (б)
В этом уравнении величины v (0); v (0); v (0) ит. п. представляют собой значения функции щ (z) иее производных, взятые в начале координат, т. е. при г = 0.
Запишем дифференциальные зависимости:
dv __ . fv __ М dz ~ *' dz- ~~ EJ ' fv _J dM __ Q _
.-/4у _ 1 _rfQ __ q (B)
dzJ ~ £7 dz ~~ EJ ' Л) 1 dq dz* EJ dz'
При дальнейшем дифференцировании имеем
_o^w_ 1 d"~4q ~dz" EJ dz"'~*'
Положим z — 0 и обозначим:
V[ (0) - E% и v' (0) — <r0 — прогиб и уголповорота в начале координат; Mi (0) = М, и Qj (0) = Qn — момент и поперечная сила в сечении,
взятой в начале координат;
<?о> <?'>> 9(1. 9о" — интенсивность нагрузки и ее производные, взятые в начале координат, т. с. при z — 0.
 Тогда на основании дифференциальных зависимостей (в) между коэффициентами ряда Маклорсна (б) и принятыми обозначениями имеем следующие равенства:
Тогда на основании дифференциальных зависимостей (в) между коэффициентами ряда Маклорсна (б) и принятыми обозначениями имеем следующие равенства:
t',(0) = ro: уН0) = фо; fi'(0) = 2J; tf'4g}-; ^'Ю) = >; ^(О)-^; ... И Т. П.
Подставляя эти значения в уравнение (б), получим
.. „ • _ _ I М» г- , Q, г3 </„ г1 q'n г:> q'' 2* _ fi
Ol = »« + фо^ + gj 2: + Е/ 3! + Ej 41 + £7 5! + Ш 6! + "' • ' ^9-6)
Полученное уравнение позволяет выразить прогибы в любом течениипервого участка через начальные параметры va, ф„, Мо, Qo ... и т. д. Часть из этих параметров известна заранее, а часть подлежит определению из граничных условий.
Для того чтобы получить уравнение прогибов оси балки на втором участке, поступим следующим образом.
По уравнению (9.6), полученному для первого участка, построим
пшию прогибов в пределах двух участков — первого и второго. На протяжении первого участка (рис. 230, г) она изображена жирной
пшией, на протяжении второго участка — пунктиром. Пунктирная
шния представляет собой изображение линии, описанной уравнением (9.6), но она не совпадает с истинной кривой оси изогнутого бруса
пя второго участка, которая проведена жирной линией. Ординаты между двумя указанными кривыми заштрихованы на чертеже. Аналитически эти ординаты выражаются равенством
Д;ч (г) = Aui = vu - Vi. (r)
Определим величину &щ, а затем найдемординаты прогибов балки на втором участке:
0и=»1+Дрг.(д)
Для этой цели напишемдва дифференциальных уравнения:
d*£j _A!i _ d2vu Ми
dz- EJ ' dz~~~~~ET'
Вычитая первое уравнение из второго, получим
Обозначив
AMi = Mu —Mi, имеем
ТШ EJ ■ w
На основании сходства дифференциального уравнения (е) с основнымуравнением (а) можно утверждать, что решение для функции щ совпадает с решением, полученным для функции (9.G).
 В этом решении вместо координаты г придется теперь брать координату, отсчитанную от точки /, т. е. (г — а^). Вместо величин Мо, Qn, <7о. •■•, и т. д. придется брать A/WF1; AQX; Aqx, ... .
В этом решении вместо координаты г придется теперь брать координату, отсчитанную от точки /, т. е. (г — а^). Вместо величин Мо, Qn, <7о. •■•, и т. д. придется брать A/WF1; AQX; Aqx, ... .
Следовательно,
JLi^i (г~а1)3 i Д(?1 (г-0')4 , A»! (z-fli)5 i /q 74
+ £i 31 n £7 4! + £7 5! "Г-"' Ф-Ц
Здесь Aui = Aui (z)—функция, определяемая равенством (г) для
второго участка (рис. 230, г); Аух — скачок в линии прогибов в точке 1 (на рис. 230, г
не показан); Асрх — скачок в угле поворота в точке / (на рис. 230, г
не показан);
АМЛ — скачок в эпюре моментов в точке / (рис. 230, б). Эта величина равна внешнему сосредоточенному моменту, приложенному в данной точке;
AQj — скачок в эпюре поперечных сил (рис. 230, в), равный внешней сосредоточенной силе, приложенной в точке /;
Aft — скачок в интенсивности нагрузки в точке /; Aq — скачок в производной от интенсивности нагрузки в точке /.
Все перечисленные здесь величины скачков определяются как разности двух значений соответствующих величин, взятых в точке 1. Так, например,
Aq^lqutf-qUzfiz^a,, (9.8)
где qw (г) и q (г)—функции, определяющие закон изменения распределенных нагрузок на втором и первом участках.
|
Величина Aq[ определяет-
а ся как разность производных;
Aq[^[q'n {z) -q (z)]z = ni = = tga3-tgcc1. (9.9)
Здесь а2 и а1 — углы наклона касательных к эпюре нагрузок, взятых в точке / (рис. 230, а).
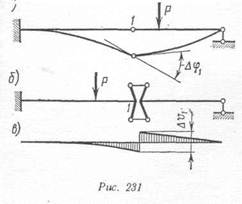
Скачок в угле поворота может иметь место в случае, если в точке / поставлен шарнир, из-за которого углы поворота слева и справа от
 гочки 1 будут различны (рис. 231, а). Скачок в прогибах возможен is том случае, если в точке 1 балка разрезана на две части, которые соединены параллельными стерженьками, как это показано на рис. 231, б. Вследствие этого прогибы двух балок в точке / будут отличаться друг от друга на Аиъ как это показано на эпюре прогибов (рис. 231, в).
гочки 1 будут различны (рис. 231, а). Скачок в прогибах возможен is том случае, если в точке 1 балка разрезана на две части, которые соединены параллельными стерженьками, как это показано на рис. 231, б. Вследствие этого прогибы двух балок в точке / будут отличаться друг от друга на Аиъ как это показано на эпюре прогибов (рис. 231, в).
Для непрерывных балок, которые по всей длине, в том числе в точке /, не имеют разрезов и полных шарниров, Аи1 = 0, Лфг = 0. Если к'перь учесть, что
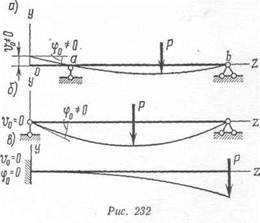
Путем дифференцирования получим универсальное уравнение . 1Я углов поворота
8 Смирнов 225
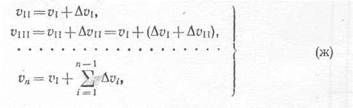
|
| и имеете с тем воспользоваться уравнениями (9.6) и (9.7), то получим |
| универсальное уравнение прогибов для произвольного участка |
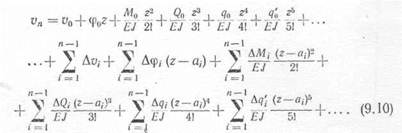
|
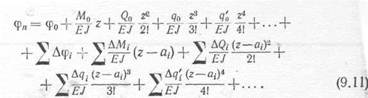
При решении каких-либо частных задач целый ряд членов, входящих в уравнения (9.10) и (9.11), равен нулю. Полученные уравнения, (9.10) и (9.11) зависят от величин и0; ц>0; Мо; Qo; qn; q'a и т. п., которые берутся в начале координат, поэтому метод решения по указанным уравнениям носит название метода начальных параметров.
Из всех перечисленных начальных параметров некоторые параметры могут быть неизвестны. Величины q0 и q'Q по условию задачи обычно заданы. Мо и Qo мог^ч бичъ известны или должны быть определены из условий статики, а в тех случаях, когда задача статически неопределима, — из условия деформаций. Величины v0 и ф0 не могут быть определены из условий статического равновесия. Определение этих начальных параметров производят по граничным условиям. Так, например, для балки, показанной на рис. 232, а, в начале координат щ и фо не равны нулю. Они могут быть определены из условий равенства нулю прогибов на опорах а и Ъ.
Основное преимущество метода начальных параметров состоит именно в том, что независимо от числа участков и нагрузки число постоянных, которые надо определить в статически определимой балке, не превышает двух.
Для балки, изображенной на рис. 232, б, начальный прогиб равен нулю, неизвестным остается начальный угол поворота %, Для его определения надо использовать условие равенства нулю прогиба на правой опоре. Для случая, представленного на рис. 232, в, начальный прогиб и начальный угол поворота равны нулю.
После того как будут найдены начальные параметры, можно написать окончательные аналитические выражения прогибов и углов поворота для каждого участка балки. Придавая величине г ряд значений и вычисляя в соответствующих точках численные значения прогибов и углов поворота, можно построить линию прогибов и линию углов поворота оси балки.
В технических задачах часто ставится вопрос об определении места и величины наибольшего прогиба балки. Для определения местоположения сечения, в котором прогиб приобретает наибольшее значение, необходимо приравнять нулю производную:
§ = Ф=0, (9.12)
откуда можно определить абсциссу наибольшего прогиба.
В некоторых случаях наибольший прогиб не совпадает с экстремальным значением функции, так, в случае, показанном на рис. 232, в, в месте наибольшего прогиба условие (9.12) не выполняется. Тогда приходится исходить из общей картины возможных деформаций систе-
 ми и определять место наибольшего прогиба путем анализа всей линии прогибов.
ми и определять место наибольшего прогиба путем анализа всей линии прогибов.
Рассмотрим ряд примеров применения универсального уравнения для определения перемещений в балке при изгибе.
1. Составить уравнения прогибов и углов поворота, а также определить место положения и величину наибольшего прогиба в балке, изображенной на рис. 233. В данной балке всего один участок, так

|
как на всем протяжении балки нет никаких изменений в нагрузке. По универсальному уравнению (9.10) с учетом того, что ~оо = 0, Q* = МП, имеем
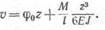

|
Для определения неизвестной величины угла поворота используем граничное условие: при z = / v — 0. Таким обоазом.
откуда находим
Следовательно, уравнение прогибов имеет вид

|
ЛифАеренципуя. получим уравнение углов поворота
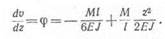
Для того чтобы определить расстояние до места наибольшего прогиба z0, воспользуемся условием
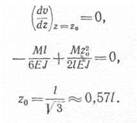
|
или
откуда
 Подставляя найденное значение г„ в уравнение (з), получим
Подставляя найденное значение г„ в уравнение (з), получим
 Интересно отметить, что этот прогиб очень мало отличается от прогиба в середине пролета:
Интересно отметить, что этот прогиб очень мало отличается от прогиба в середине пролета:
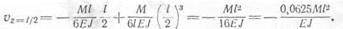
|
 2. Написать уравнение прогибов и углов поворота для балки, показанной на рис. 234, и определить наибольший прогиб.
2. Написать уравнение прогибов и углов поворота для балки, показанной на рис. 234, и определить наибольший прогиб.

|
Поместив начало координат в заделку, имеем:

|
Для первого участка по формуле (9.10) получаем уравнениепрогибов
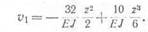
Это уравнение справедливо для случаев, когда 0 «ё г^ „ . К точке 1
примыкают два участка: на первом участке в точке 1 q = 0, на втором участке в этой же точке q — — qv При переходе через точку / от первого ко второму участку нагрузка изменяется от 0 до — qx. Следовательно, Aqx = — <7j. Для того чтобы не сделать ошибки в определении величин и знаков At?i и A^J, следует пользоваться формулами (9.8) и (9.9).
По этим формулам находим

Скачки в моменте и поперечной силе отсутствуют АУИХ = О, AQ, = 0.
Применяя формулу (9.10), получим уравнение для прогибов на втооом участке

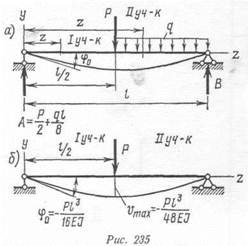
 Уравнения углов поворота получим дифференцированием урав-
Уравнения углов поворота получим дифференцированием урав-
|
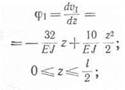
|
| для второго участка |

|
нений прогибов: для первого участка
Наибольший прогиб vmRX пудет на правом конце бал-
ки; подставляя г = I = 4 м в уравнение прогибов для второго участка, получим
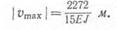
Так как в решении размеры балки принимались в метрах и на-i рузка — в тоннах на погонный метр, то величины Е и J надо брать I'. тс/м2 и л*.
3. Написать уравнение прогибов балки, показанной на рис. 235, а, и определить прогиб посередине пролета.
Начальные параметры для данной задачи имеют следующие значения:
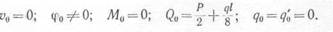
Для первого участка согласно универсальному уравнению прогиб
определяют по формуле
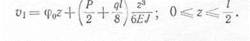
В точке перехода от участка / к участку // имеем
ДМХ = О; AQ1 = —P; bq^-q; &q[ = Следовательно,
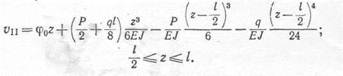
В полученных уравнениях прогибов неизвестна величина ф0. Для ее определения используем условие, что на правой опоре прогиб равен нулю; так как правая опора принадлежит второму участку, то, подставляя г = / в уравнение прогибов второго участка и приравнивая прогиб нулю, получим
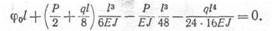
|
Решая это уравнение относительно ср0, найдем

|
Подставив значение ф0 в уравнения прогибов, окончательно получим:
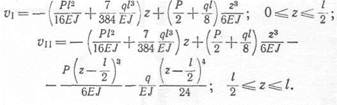
|
Найдем теперь прогиб посередине пролета. Положив г = -к- по первому уравнению, получим
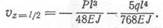
|
Данную величину можно определить также и из второго уравнения, так как середина пролета принадлежит и второму участку. Легко
заметить, что два последних члена второго уравнения при г = й