Динамический расчет системы методом перемещений.

 

Порядок расчета:

1. Анализируем схему и выбираем основную систему.

2. Строится изгибающий момент.

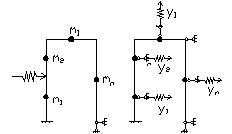
Для заданной системы основная получилась путем введения связей по направлению неизвестных перемещений z₁, z₂ … z_n cсоответствующих масс m₁, m₂ …m_n. число степеней свободы упругой системы определяется числом возможных независимых смещений. Получаем систему уравнений: (1)

Частное решение системы:

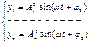(2)

A₁, A_n – амплитуды колебаний соотв. масс, φ₀ – нач. фаза колебаний.

Возьмем вторую производную по времени t:

(3)

Подставляем из ур-я (3) и (2)в (1):

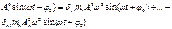
Перобразовываем:

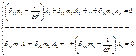
1/ω²=λ

Если А₁=А₂=…=А_n=0 (сист-ма наход. в покое) Если А₁≠А₂≠А_n, тогда когда определитель из коэф-ов при амплитудах=0.

Вековое ур-ие с n-степенью свободы.

Раскрываем полученный определитель. Если вековое уравнение 2-го или 3-го порядка его решение достаточно просто, но при дальнейшем увеличении порядка решение становится затруднительным.
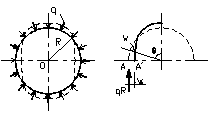
35. Устойчивость кругового кольца при гидростатич. давлении.

До потери устойчивости все сечения кольца испытывают только сжатие и продольная сила равна N=qR. При достижении нагрузкой критического значения может произойти потеря устойчивости и кольцо примет слегка изогнутую форму, к-ая будет формой равновесия. Рассмотрим изогнутую равновесную форму с двумя осями симметрии. ДУ изгиба бруса кругового очертания: 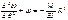. Изгибающий момент в точке А΄ равен M₀=qRω₀, а изгиб. момент в произвольной точке kM=qRω. Подставляя в ДУ и после небольшого преобразования. 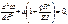обозначив через получим общее решение этого однородного диф. уравнения в след. виде.

Граничные условия:

1) при θ=0 откуда B=0;

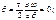
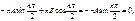
2) при 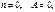т.к. ω не обращается тождественно в ноль, следовательно, 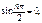что дает минимальное значение n_min=2. Таким образом, минимальная критическая нагрузка, соответ. данной форме потери устойчивости, определяется из условия .