рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Туризм
- /
- Ошибки выборочного наблюдения
Реферат Курсовая Конспект
Ошибки выборочного наблюдения
Ошибки выборочного наблюдения - раздел Туризм, Статистика туризма Учебное пособие При Любом Наблюдении (Сплошном И Несплошном) Возникают Ошибки При Регистрации...
При любом наблюдении (сплошном и несплошном) возникают ошибки при регистрации единиц наблюдения. Такие ошибки называются ошибками регистрации. Они могут быть случайными и систематическими, это связано в значительной степени с субъективным фактором, который всегда присутствует при организации и проведении наблюдения.
При проведении выборочных наблюдений, помимо ошибок регистрации, возникают случайные ошибки репрезентативности (представительности), которые возникают в связи с тем, что отобранная для наблюдения часть общей совокупности имеет отличную от генеральной n
Научным обоснованием случайных ошибок выборки являются теория вероятностей и ее предельные теоремы. Используются теоремы русских математиков П.Л. Чебышева и А.М. Ляпунова. В соответствии с этими теоремами, с увеличением численности выборки размеры случайных ошибок сокращаются, что при достаточно большом объеме выборки случайная ошибка будет сколь угодно мала и что характеристики выборочного наблюдения будут надлежащим образом представлять генеральную совокупность.
Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки  . Под средней ошибкой выборки понимают расхождение между средними выборочной и генеральной совокупности (
. Под средней ошибкой выборки понимают расхождение между средними выборочной и генеральной совокупности ( , которое не превышает
, которое не превышает  . В математической статистике доказано, что значение средней ошибки выборки определяются по формуле:
. В математической статистике доказано, что значение средней ошибки выборки определяются по формуле:
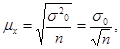 где
где 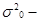 дисперсия изучаемого признака х в выборочной совокупности, а n – численность выборочной совокупности.
дисперсия изучаемого признака х в выборочной совокупности, а n – численность выборочной совокупности.
Соответственно для расчета средней ошибки доли изучаемого признака используется формула:
 где pq – где дисперсия доли изучаемого признака, а n – численность выборочной совокупности. Следовательно, для уменьшения средней ошибки выборки в 3 раза необходимо увеличить объем выборки в 9 раз.
где pq – где дисперсия доли изучаемого признака, а n – численность выборочной совокупности. Следовательно, для уменьшения средней ошибки выборки в 3 раза необходимо увеличить объем выборки в 9 раз.
Рассмотрим условный пример. Генеральная совокупность – число сделок N =1000
Доходность сделок (тыс. руб.) Число сделок
12 200
14 500
15 300
Всего: 1000
Средня доходность:
 тыс. руб.
тыс. руб.
Дисперсия: 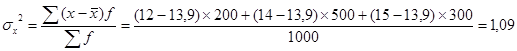
Доля сделок с доходностью 14 и более тыс. рублей р=
 или 80%
или 80%
Предположим, что случайным образом отобрана информация о 200 сделках и получены данные о средних и относительных показателях:
Доходность сделок (тыс. руб.) Число сделок
12 34
14 100
15 66
Всего: 200
Средняя доходность  тыс. руб.
тыс. руб.
Дисперсия 
Доля сделок с доходностью 14 и более тыс. рублей w=
 или 83%.
или 83%.
Сведем полученные показатели в таблицу:
|
Теперь можно определить среднюю ошибку выборки:
Для средней доходности 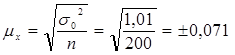 ;
;
Для доли 14 и более т. руб.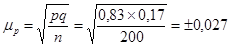 .
.
– Конец работы –
Эта тема принадлежит разделу:
Статистика туризма Учебное пособие
Министерство образования и науки Российской Федерации... Федеральное агентство по образованию... Санкт Петербургский государственный университет сервиса и экономики...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Ошибки выборочного наблюдения
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов