Постановка и метод решения задачи о многополюсной кратчайшей цепи
Рассмотрим задачу нахождения кратчайших цепей между всеми парами узлов сети.
Кратчайшей цепью между двумя произвольными узлами является цепь, стоимость единицы потока по которой минимальна.
Поскольку направление потока в неориентированных дугах нельзя определить заранее, то каждую такую дугу следует заменить двумя ориентированными дугами с противоположными направлениями и длинами (стоимостями), равными длине неориентированной дуги. Предполагается, что длины луг могут быть как положительными, так и отрицательными. Однако длина, или стоимость, каждого цикла или контура должна быть неотрицательной. Алгоритм решения данной задачи разработан Флойдом.
Пусть N = {1,2,..., n} – множество узлов, а ci j – количественный параметр (длина, стоимость) дуги (i, j), направленной от узла i к узлу j. Обозначим через 
длину кратчайшей цепи из узла i в узел k.
Алгоритм Флойда. Первоначально за оценку длины di k кратчайшей цепи между двумя произвольными узлами i и k (между которыми могут быть и промежуточные узлы) принимают длину дуги (i, k), соединяющей эти узлы. Затем последовательно проверяют всевозможные промежуточные узлы, расположенные между i и k. Если длина цепи, проходящей через некоторый промежуточный узел, меньше текущего значения di k, то переменной di k присваивают новое значение; если di k > di j + dj k, то значение di k заменяют значением (di j + dj k). Такую процедуру повторяют для различных пар узлов, пока не будут получены все значения .
В алгоритме Флойда начальным значением переменной di k является ci k. Затем оно последовательно улучшается до тех пор, пока не будет найдена кратчайшая цепь между узлами i и k. Алгоритм Флойда позволяет решать задачу о многополюсной кратчайшей цепи (пути) для сети из п узлов за п итераций. Обозначим символом 
оценку длины кратчайшей цепи из узла i в узел k, полученную на j-й итерации, и рассмотрим следующую задачу.
Задача. Необходимо соединить восемь объектов многополюсной цепью кратчайшей длины, причём один из объектов (№ 8) может только направлять информацию, а остальные – и направлять, и получать информацию без каких-либо ограничений (рис.2.3.1). На рисунке каждый объект представлен узлом, а каждая линия – дугой. Ориентированные дуги соответствуют распределительным звеньям, которые могут быть использованы для передачи информации только в указанном направлении. Числа, приписанные дугам, соответствуют расстоянию между объектами. Требуется найти для каждого объекта кратчайшие пути, связывающие его с другим объектами.
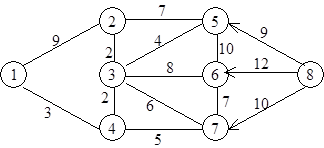
Рис.2.3.1
Решение. Воспользуемся алгоритмом Флойда. Поскольку п = 8, то число итераций в алгоритме будет 8. На каждой итерации строят матрицы длин кратчайших путей, которые содержат текущие оценки длин кратчайших цепей D j= ||||, где D0 = ||ci k||, и матрицу маршрутов R j, служащую для нахождения промежуточных узлов (если таковые имеются) кратчайших цепей. На j-й итерации матрица маршрутов определяется как R j = ||
||, где - первый промежуточный узел кратчайшей цепи из i в k, выбираемый среди множества
{1,2,..., j}, i ¹ j ¹ k, R 0 = ||
||,
где = k.
Узел может быть получен из следующего соотношения:
Строим матрицу длин кратчайших цепей D0 и матрицу маршрутов R0. Отсутствие связи помечаем знаком ¥, нулём обозначаем связи внутри одного узла (из узла i в узел i):
;
.
Итерация 1. Выбираем базовый узел j = 1. В матрице D0 вычёркиваем j-ю (базовую) строку и j-й (базовый) столбец. Чтобы определить, приведёт ли использование узла 1 к более коротким цепям, необходимо исследовать элементы матрицы D0 с помощью трёхместной операции: 
; i ¹ j ¹ k. Если = ¥, т.е. j-й элемент базового столбца равен ¥, то = 
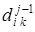. Если 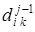= ¥, т.е. j-й элемент базовой строки равен ¥, то = 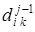. Если 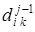¹¥ и одно из двух значений 
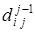или 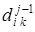превосходит 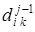, то замену также производить не следует. Столбцы 3, 5, 7 и 8 содержат элементы, равные ¥ и принадлежащие базовой строке, а строки 3, 5-8 – элементы, равные ¥ и принадлежащие базовому столбцу, т.е. исследовать надо элементы (2,2); (2,4); (4,2); (4,4). Поскольку диагональные элементы можно не рассматривать, необходимо исследовать лишь оценки 
и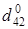 
:
;
.
Оценки 
и 
меньше оценок и 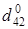: и должны быть внесены в матрицу D1, а в матрице маршрутов надо положить 
, 
=1 и 
=1. Остальные элементы матриц D0 и R0 остаются без изменений.
Получим матрицы
;
.
Итерация 2. Определим узел 2 как базовый, т.е. проверим, приведёт ли его использование к более коротким цепям, и вычеркнем в матрице D1 вторую строку и второй столбец. Здесь столбцы 6-8 содержат элементы, равные ¥ и принадлежащие базовой строке, а строки 6-8 – элементы, равные ¥ и принадлежащие базовому столбцу (столбцы и строки 6-8 не рассматриваем). Исключаем и диагональные элементы. Остаётся исследовать лишь элементы (1,3), (1,4), (1,5), (3,1), (3,4), (3,5), (4,1), (4,3), (4,5), (5,1), (5,23), (5,4). Нетрудно проверить, что здесь улучшены могут быть только оценки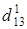 
, 
, 
, 
, 
, 
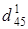, равные ¥:
;
;
;
;
;
.
Таким образом, 
; остальные элементы 
остаются без изменения. Новые матрицы имеют вид
;
.
Итерация 3. Определяем, приведёт ли использование узла 3 к более коротким цепям. Берём узел 3 в качестве базового и вычеркиваем третью строку и третий столбец в матрице D2. Исключаем диагональные элементы, элементы третьего столбца и третьей строки. Исследуем оставшиеся элементы матрицы D2, получаем матрицы D3 и R3. Аналогично получаем матрицы D j и R j, j=
. Матрицы D j, R j, j =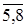
остаются без изменений. Следовательно, оптимальное решение соответствует матрицам D5 и R5, определяющим как оптимальное расстояние для передачи между объектами, так и последовательность передачи информации:
;
.
Например, определим кратчайшую цепь из узла 1 в узел 5. По матрице D5 определяем, что длина этой цепи равна 
=9. Чтобы найти соответствующую последовательность узлов, обратимся к матрице R5. Значение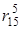 
равно 4, т.е. узел 4 является первым промежуточным узлом в кратчайшей цепи из узла 1 в узел 5. Теперь надо определить, какой узел следует за узлом 4 в кратчайшей цепи из узла 4 в узел 5. Рассмотрим 
данное значение равно 3. Значит, за узлом 4 следует узел 5. Аналогично, за узлом 3 следует узел 3, так как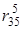 
= 5. Следовательно, кратчайшая цепь из узла 1 в узел 5 определяется последовательностью узлов 1, 4, 3, 5.
3. Методические указания по выполнению лабораторной работы
Перед выполнением лабораторной работы необходимо ознакомиться с её целью, основными теоретическими положениями, особенностями использования пакета прикладных программ (ППП) QSB и табличного процессора (ТП) Excel 7.0 при решении транспортных задач.
Каждый студент получает у преподавателя индивидуальное задание на выполнение лабораторной работы.
В процессе лабораторной работы необходимо:
1) на основе содержательной постановки транспортной задачи разработать её математическую модель;
2) подготовить исходные данные для решения транспортной задачи методом потенциалов с использованием ППП QSB и симплекс-методом с использованием ТП Excel 7.0;
3) решить транспортную задачу при фиксированном варианте задания исходных данных;
4) провести исследование влияния изменения вариантов задания исходных данных на результаты решения транспортной задачи. При этом проводится изменение коэффициентов целевой функции, изменение числа ограничений и переменных, изменение запасов и потребностей в соответствующей транспортной задаче.
На основе проведённых исследований определяются границы устойчивости полученных решений транспортной задачи.
Результаты расчётов и исследований выдаются на печать в виде соответствующих таблиц, номограмм и графиков. Отчётный материал предоставляется преподавателю и результаты выполненной работы защищаются.
4. форма отчётности по выполненной лабораторной работе
Отчёт должен содержать:
- титульный лист;
- содержательную и формальную постановку транспортной задачи;
- распечатки результатов решения и исследования транспортной задачи с использованием ППП QSB и ТП Excel 7.0;
- выводы по результатам решения и исследованию транспортной задачи.
Отчёт о лабораторной работе представляется к моменту её защиты.