Основные определения
Граф  – это совокупность двух множеств: вершин
– это совокупность двух множеств: вершин 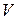 и ребер
и ребер 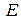 , между которыми определено отношение инцидентности.
, между которыми определено отношение инцидентности.
Каждое ребро e из E инцидентно ровно двум вершинам  и
и  , которые оно соединяет. При этом вершина
, которые оно соединяет. При этом вершина  и ребро e называются инцидентными друг другу, а вершины
и ребро e называются инцидентными друг другу, а вершины  и
и  называются смежными.
называются смежными.
Принято обозначение n для числа вершин графа (мощность множества 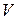 ):
):  и m для числа его ребер:
и m для числа его ребер:  . Говорят, что граф G есть (n, m) граф, где n – порядок графа, m – размер графа.
. Говорят, что граф G есть (n, m) граф, где n – порядок графа, m – размер графа.
Если все ребра  графа неориентированные, т.е. пары вершин, определяющие элементы множества E, неупорядочены, то такой граф называется неориентированным графом, или неографом. На рис. 12.1 показан пример неографа. Этот граф имеет пять вершин и шесть ребер.
графа неориентированные, т.е. пары вершин, определяющие элементы множества E, неупорядочены, то такой граф называется неориентированным графом, или неографом. На рис. 12.1 показан пример неографа. Этот граф имеет пять вершин и шесть ребер.

Рис. 12.1
Маршрут – последовательность ребер, в которой каждые два соседних ребра имеют общую вершину. Граф связен, если любые две вершины соединены хотя бы одним маршрутом. Число ребер маршрута определяет его длину.
Ребра, инцидентные одной паре вершин, называются параллельными или кратными. Граф с кратными ребрами называется мультиграфом.
Ребро  называется петлей (концевые вершины совпадают). Граф, содержащий петли и кратные ребра, называется псевдографом. На рис. 12.2 показан псевдограф.
называется петлей (концевые вершины совпадают). Граф, содержащий петли и кратные ребра, называется псевдографом. На рис. 12.2 показан псевдограф.

Рис. 12.2
Степень deg(v) вершины – это число ребер, инцидентных v. В неографе сумма степеней всех вершин равна удвоенному числу ребер (лемма о рукопожатиях):
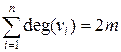 . (12.1)
. (12.1)
Петля дает вклад, равный 2, в степень вершины.
Степенная последовательность – последовательность степеней всех вершин графа, записанная в определенном порядке (по возрастанию или убыванию).
Пример 12.1. Степенная последовательность неографа, изображенного на рис. 12.1, записанная по возрастанию, выглядит так:
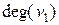 =1,
=1,  =2,
=2, 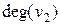 =3,
=3,  =3,
=3,  =3.
=3.
Сумма степеней всех вершин графа равна:
 .
.
Этот результат не противоречит лемме о рукопожатиях, поскольку граф имеет шесть ребер (m = 6).
Матрица смежности графа – квадратная матрица A порядка n, где элемент  равен числу ребер, соединяющих вершины i и j.
равен числу ребер, соединяющих вершины i и j.
Пример 12.2. Граф, показанный на рис. 12.1, имеет следующую матрицу смежности
 .
.
Матрица инцидентности I – еще один способ описания графа. Число строк этой матрицы равно числу вершин, число столбцов – числу ребер;  =1, если вершина v инцидентна ребру e; в противном случае
=1, если вершина v инцидентна ребру e; в противном случае  =0. В каждом столбце матрицы инцидентности простого графа (без петель и без кратных ребер) содержится по две единицы. Число единиц в строке равно степени соответствующей вершины.
=0. В каждом столбце матрицы инцидентности простого графа (без петель и без кратных ребер) содержится по две единицы. Число единиц в строке равно степени соответствующей вершины.
Пример 12.3. Граф, показанный на рис. 12.1, имеет следующую матрицу инцидентности
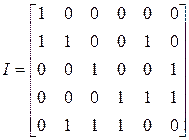 .
.
Граф 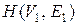 называется подграфом графа
называется подграфом графа  , если
, если  и
и  . Если
. Если  , то подграф называется остовным.
, то подграф называется остовным.
Компонента связности графа – максимальный по включению вершин и ребер связной подграф.
Ранг графа 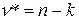 , где k – число компонент связности.
, где k – число компонент связности.
Дерево – связной граф, содержащий n – 1 ребро.
Пример 12.4. На рис. 12.3 показано дерево, которое одновременно является остовным подграфом графа, показанного на рис. 12.1.

Рис. 12.3