Раскраска графа, хроматический полином

Предположим, что перед нами стоит задача: раскрасить карту мира так, чтобы каждая страна имела свой собственный цвет. Поскольку на свете существует несколько сотен государств, то, естественно, потребуется достаточно много разных красок.

Упростим задачу. Будем использовать меньшее количество красок, но при этом не будем допускать, чтобы соседние страны, имеющие общие границы, были окрашены в один цвет. Возникает вопрос: какое минимальное количество красок требуется, чтобы удовлетворить этому условию?

Ответить на этот вопрос можно с помощью теории графов. Для этого нужно представить карту мира в виде графа, каждая вершина которого соответствует отдельной стране, а ребро между смежными вершинами соответствует наличию между странами общей границы.

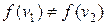Произвольная функция на множестве вершин графа называется раскраской графа. Раскраска называется правильной, если для любых смежных вершин и . Минимальное число k, при котором граф G является k-раскрашиваемым называется хроматическим числом графа .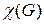

Граф называется пустым, если в нем удалены все ребра и вершины изолированы друг от друга. Граф называется полным, если в нем нельзя добавить новое ребро, не добавив при этом одновременно новую вершину.

Теорема 12.7 (Брукса). Для любого графа G, не являющегося полным, 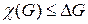, если 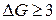– максимальная из степеней вершин графа.

Для определения количества способов раскраски графа в x цветов, необходимо составить хроматический полином P(G, x). Значение полинома при некотором конкретном 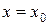равно числу правильных раскрасок графа в 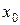цветов.

Существует лемма, утверждающая, что хроматический полином графа имеет вид

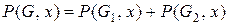, (12.4)

где – граф, полученный из G добавлением ребра (u, v), а граф 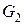получается из G отождествлением вершин u и v.

Другой вариант леммы:

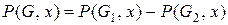, (12.5)

где – граф, полученный из G удалением ребра (u, v), а граф 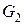получается из G отождествлением вершин u и v.

Операцию отождествления вершин u и v называют также стягиванием ребра (u, v).

Оба варианта леммы составляют основу для хроматической редукции графа (reduction – «сокращение» на английском). Хроматическая редукция графа – представление графа в виде нескольких пустых или полных графов, сумма хроматических полиномов которых равна хроматическому полиному графа. Очевидно, что хроматический полином пустого графа равен 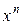(каждая вершина может быть раскрашена независимо от других), а для полного графа 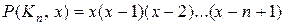. Последнее выражение называют факториальной степенью переменной x: .

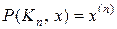Разложения по пустым и полным графам связаны. Факториальную степень можно представить в виде полинома:

, (12.6)

где 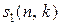– числа Стирлинга первого рода. И наоборот, степень 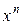можно выразить через факториальные степени:

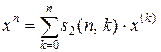, (12.7)

где – числа Стирлинга второго рода, обладающие следующими свойствами:

при 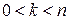, (12.8)

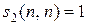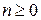при , при .

При получении хроматического полинома могут быть полезны следующие теоремы.

Теорема 12.8. Коэффициенты хроматического полинома составляют знакопеременную последовательность.

Теорема 12.9. Абсолютная величина второго коэффициента хроматического полинома равна числу ребер графа.

Теорема 12.10. Наименьшее число i, для которого отличен от нуля коэффициент при 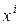в хроматическом полиноме графа G, равно числу компонент связности графа G.

Кроме вершинной раскраски, существует еще реберная раскраска и раскраска граней.

Пример 12.7. Найти хроматический полином графа, показанного на рис. 12.8.

Рис. 12.8

Решение. В зависимости от числа ребер графа можно использовать разложение (12.4) или (12.5). Если граф почти полный, то, добавив несколько ребер по разложению (12.4), получим хроматический полином в виде суммы факториальных степеней. Если же ребер мало и для получения пустого графа требуется удалить только несколько ребер, то следует использовать разложение (12.5) с удалением ребер. Такие действия называются хроматической редукцией.

1. Хроматическая редукция по пустым графам. Воспользуемся вначале леммой (12.5). Удаляя ребра и отождествляя соответствующие вершины (стягивая ребра), сведем исходный граф к пустым графам. Сначала разложим граф на два, убрав, а затем стянув ребро 1-3. Выполненное действие запишем в виде условного равенства:

Здесь операция вычитания относится не к самому графу, а к его хроматическому полиному. Таким образом, последнее равенство означает, что 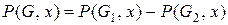. Для сокращения записи обозначение P(…) будем опускать. Далее разложим каждый из графов и 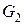, пользуясь той же леммой.

Приведем подобные члены:

(12.9)

В итоге получим искомый хроматический полином:

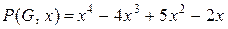. (12.10)

Разложение (12.9) называется хроматической редукцией графа по пустым графам.

Очевидно, что результат соответствует утверждениям теорем 12.8-12.10. Коэффициенты в (12.10) образуют знакопеременную последовательность, а коэффициент при равен четырем – числу ребер. Наименьшая степень x в полиноме равна 1, т.е. числу компонент связности графа.

2. Хроматическая редукция по полным графам. Добавив к изображенному на рис. 12.8 графу ребро 1–4, получим граф с большим числом ребер. Затем в исходном графе отождествим вершины 1 и 4. В результате получим два графа.

Отождествление вершин приводит к уменьшению порядка и иногда размера графа. Второй граф – это полный граф 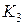, его преобразовывать больше не требуется. К первому графу добавим ребро 1–2 и отождествим вершины 1 и 2:

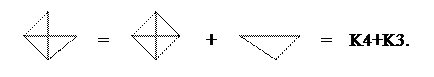
В итоге получим

(12.11)

Хроматический полином примет вид

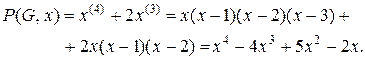(12.12)

Разложение (12.11) называется хроматической редукцией графа по полным графам.

Оба способа дали один результат, и из редукции по полным графам легко получить редукцию по пустым. Для этого достаточно раскрыть скобки и привести подобные члены, как в (12.12). Однако обратное действие не очевидно. Для того чтобы полином , полученный из пустых графов, выразить в виде суммы факториальных степеней, необходимы числа Стирлинга 2-го рода. Согласно рекуррентным формулам (12.8) имеем следующие числа:

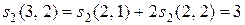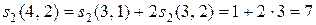Пользуясь (12.7) и найденными числами Стирлинга 2-го рода, получим

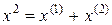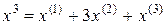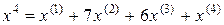Произведем преобразование хроматического полинома:

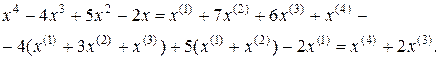
Хроматическое число 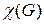графа лучше всего получить, разложив хроматический полином на множители:

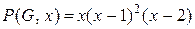Минимальное натуральное число x, при котором не обращается в нуль, равно 3. Отсюда следует 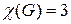. Так как максимальная степень вершин графа 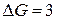, выполняется оценка .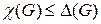