Транзитивное замыкание

Прямым (декартовым) произведением множеств A и B называется множество . Бинарное отношение на X – любое подмножество прямого произведения: .

Отношение на X рефлексивно, если для любого пара .

Отношение на X антирефлексивно, если для любого пара .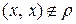

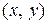Отношение на X симметрично, если для любой пары из условия следует .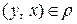

Отношение на X антисимметрично, если из условий и 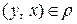следует x = y.

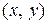Отношение на X асимметрично, если для любой пары из условия следует .

Отношение на X транзитивно, если для любых двух пар 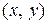и из условий и 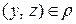следует .

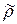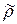Отношение называется замыканием отношения на свойство A, если обладает свойством A, 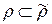и для любого отношения 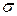со свойством A справедливо вложение .

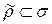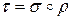Композицией бинарных отношений и называют отношение , состоящее из пар 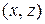, таких, что и .

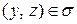Транзитивное замыкание отношения имеет вид 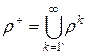, где , .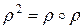

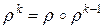Теорема 13.1. Отношение транзитивно тогда и только тогда, когда .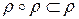

Граф есть отношение на множестве вершин. Элементами этого отношения являются дуги (или ребра, если отношение симметрично).

Орграф называется транзитивным, если для любых его дуг 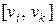и существует замыкающая дуга .

Пример 13.2. Дано отношение, заданное матрицей

Исследовать отношение на симметрию, антисимметрию, асимметрию, рефлексивность, антирефлексивность. Найти транзитивное замыкание отношения. Построить граф отношения и его транзитивного замыкания.

Решение.

1. Данное отношение не является симметричным, так как матрица несимметрична. Например, пара (2, 1) принадлежит , а пара (1, 2) ему не принадлежит.

2. Отношение антисимметрично, так как нет ни одной пары , .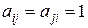

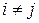3. Отношение антисимметрично, но не асимметрично, так как на диагонали матрицы имеются элементы, равные 1.

4. Все диагональные элементы матрицы рефлексивного отношения равны 1. Данное отношение не является рефлексивным.

5. Отношение не обладает свойством антирефлексивности, так как диагональ матрицы ненулевая.

6. Данное отношение не является транзитивным, так как, например, пары (1, 4) и (4, 3) принадлежат , а пара (1, 3) ему не принадлежит.

Найдем транзитивное замыкание графа, заданного отношением . Процедура транзитивного замыкания сводится к добавлению в матрицу смежности минимального числа единиц, так, чтобы соответствующее отношение обладало свойством транзитивности. Для этого выполняем следующие операции.

1. Вычисляем матрицу композиции 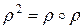. Для этого умножаем (с использованием операции логического умножения) матрицу A саму на себя: 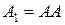. Такое произведение называется произведением булевых матриц. Результат произведения получают следующим образом. Элемент результирующей матрицы 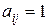, если хотя бы в одном случае k-й элемент i-й строки первого сомножителя и k-й элемент j-го столбца второго сомножителя одновременно равны единице. В противном случае .

.

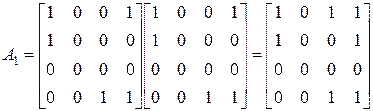2. Находим логическую сумму (дизъюнкцию) матриц. Поэлементная дизъюнкция матриц дает:

.

3. Сравним 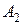с A. Если 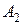= A, то 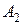– искомая матрица. Если 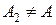, то полагаем , возвращаемся к п. 1 и повторяем всю процедуру для новой матрицы. В данном случае 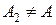. Поэтому принимаем:

.

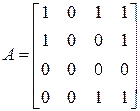Умножаем матрицу саму на себя:

.

Находим логическую сумму:

.

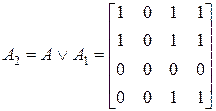Сравниваем: 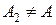. Полагаем и повторяем процедуру еще раз.

.

.

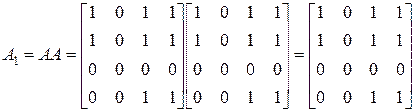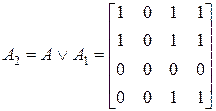Сравниваем: 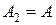. Следовательно, 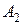– матрица транзитивного замыкания заданного отношения.

На рис. 13.2 (а и б) представлены графы отношения и его транзитивного замыкания. Диагональные элементы матрицы соответствуют петлям на графе. Матрица несимметрична, поэтому граф отношения – ориентированный.

Рис. 13.2