Упорядоченные бинарные деревья и приоритетные очереди
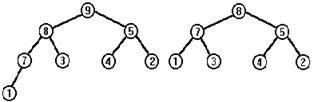
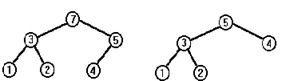
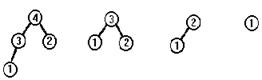
Упорядоченным бинарным деревом, или бинарным деревом поиска, называют дерево, в любой части которого элементы левого поддерева меньше корневого элемента, а элементы правого поддерева больше корневого элемента. Обычно предполагается, что все элементы дерева уникальны; если это не так, то достаточно одно из вышеприведенных неравенств заменить на нестрогое. Если ожидается, что в дереве будет много одинаковых элементов, то лучше предусмотреть в каждой вершине дополнительное поле - счетчик, и при включении элемента, который уже есть в дереве, не создавать новую вершину, а увеличивать значение счетчика в уже существующей. Упорядоченные бинарные деревья широко применяются в задачах сортировки, поиска и хранения информации. Данные, организованные таким образом, обладают замечательным свойством: для того чтобы найти заданный элемент, удалить элемент или добавить новый, требуется всего C×log2(n) операций (правда, если дерево достаточно сбалансировано - о сбалансированности деревьев мы поговорим ниже), а алгоритмы логарифмической сложности являются самыми быстрыми среди всех возможных алгоритмов, это утверждение можно строго доказать. Не углубляясь пока в детали алгоритма, рассмотрим на примере процесс формирования бинарного дерева поиска. В начальный момент дерево пусто. Пусть элементы включаются в дерево в такой последовательности: 4,1,8,9,3,5,2,7. Первый элемент помещается в корень дерева, со всеми остальными поступаем следующим образом: начинаем поиск места для нового элемента с корня, если элемент меньше корневого и левое поддерево не пусто, то ищем для него место в левом поддереве, в противном случае - в правом поддереве; поступаем так, пока не найдем место, где должен находиться новый элемент (или пока не найдем элемент, равный ему). Проиллюстрируем этот алгоритм рисунком, на котором показаны последовательные стадии формирования дерева для нашей входной последовательности.

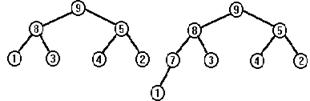
Чтобы вставить очередной элемент, нам требовалось выполнить не больше операций, чем текущая высота дерева, столько же операций потребуется, чтобы найти нужный элемент в уже сформированном дереве. Если дерево строго бинарное, то его высота и количество элементов в нем связаны соотношением n=2h-1 или h=log2(n+1). Таким образом, все эти алгоритмы имеют сложность log2(n). На практике обеспечить строгую бинарность дерева, конечно, невозможно, поэтому стремятся не к строгой бинарности, а к сбалансированности дерева. Понятие “сбалансированное дерево” можно определить по крайней мере двумя разными способами. Дерево сбалансировано, если для каждой его вершины высота левого поддерева и высота правого поддерева отличаются не более чем на k. Или: дерево сбалансировано, если для любой его вершины количество вершин в левом и правом поддереве отличается не более, чем на k. Назовем деревья первого вида h(k)-сбалансированными, а деревья второго вида - n(k)-сбалансированными. Дерево, показанное на рисунке, является h(1)-сбалансированным и n(1)-сбалансированным. Но если бы элементы поступали в дерево в порядке возрастания или в порядке убывания, то все дерево состояло бы из одной, но очень длинной ветви и было бы очень плохо сбалансированным. Можно строго показать, что для достаточно сбалансированных деревьев логарифмическая сложность алгоритмов включения и поиска сохраняется. Но проблема заключается в том, что при включении нового элемента в сбалансированное дерево его сбалансированность может ухудшаться, тогда необходимо каким-то образом преобразовать дерево, чтобы восстановить сбалансированность, причем это надо сделать алгоритмом сложности не более, чем log2(n), в противном случае теряется смысл использования таких деревьев; h(1)- сбалансированные деревья имеют специальное название “АВЛ-деревья“, алгоритмы их обработки, не нарушающие сбалансированность, известны. Здесь мы не будем подробно обсуждать эти вопросы, предположим лишь, что элементы включаются в дерево в достаточно случайной последовательности и, следовательно, дерево будет достаточно хорошо сбалансировано. Запишем процедуру, которая добавляет элемент в упорядоченное бинарное дерево, будем считать, что все элементы в дереве уникальны, и не будем включать новый элемент, если он уже есть в дереве.
Procedure Add_Bin_Tree(Var Root:PTree; Ch:Char);
Var p,pc : Ptree;
Begin
If Root=Nil Then Begin {дерево пусто, создаем корень}
New(Root);
Root^.I:=Ch;
Root^.L:=Nil;
Root^.R:=Nil;
Root^.U:=Nil;
Exit;
End;
{ищем место для нового элемента или сам этот элемент}
p:=Root;
While (p^.L<>Nil)And(Ch<p^.I)Or(p^.R<>Nil)And(Ch>p^.I) Do
If Ch<p^.I Then p:=p^.L Else p:=p^.R;
If Ch=p^.I Then Exit; {такой элемент есть - ничего не делаем}
New(pc);
{создаем новую вершину дерева и записываем туда включаемый элемент}
pc^.I:=Ch;
pc^.L:=Nil; pc^.R:=Nil;
pc^.U:=p;
If Ch<p^.I Then p^.L:=pc Else p^.R:=pc;
End;
Этот алгоритм можно записать и рекурсивной процедурой. Алгоритм поиска элемента в упорядоченном бинарном дереве уже содержится в процедуре Add_Bin_Tree, и мы не станем его выписывать отдельно. Чтобы успешно пользоваться упорядоченными бинарными деревьями, нужно еще научиться удалять элементы из дерева, не нарушая его упорядоченности. Если удаляемая вершина - лист, то алгоритм удаления тривиален. Если удаляемая вершина не имеет левого поддерева, то запишем на ее место ее правого потомка. Аналогично, если вершина не имеет правого поддерева, то запишем на ее место ее левого потомка. В случае, когда у вершины есть и левое и правое поддерево, поступим следующим образом: найдем наименьший элемент, больший удаляемого, для этого сделаем один шаг вправо, а затем будем двигаться все время влево, пока не достигнем вершины без левого поддерева. Поменяем местами элементы, записанные в удаляемой и найденной нами вершинах и удалим найденную вершину как не имеющую левого поддерева. Конечно, можно использовать и симметричный алгоритм, в котором ищется наибольший элемент, меньший удаляемого.
Procedure Del_Bin_Tree(Var Root:PTree; Ch:Char);
Var p,pp : Ptree;
Begin
If Root=Nil Then Exit;
{ищем в дереве элемент Ch}
p:=Root;
While (p^.L<>Nil)And(Ch<p^.I)Or(p^.R<>Nil)And(Ch>p^.I) Do
If Ch<p^.I Then p:=p^.L Else p:=p^.R;
If Ch<>p^.I Then Exit; {элемент не найден, ничего не делаем}
If p^.L=Nil Then Begin {Нет левого потомка}
If p^.U=Nil Then Root:=p^.R {Удаляем корень}
Else {не корень}
If p^.U^.L=p Then p^.U^.L:=p^.R
Else p^.U^.R:=p^.R;
If p^.R<>Nil Then p^.R^.U:=p^.U;
End
Else
If p^.R=Nil Then Begin {Нет правого потомка}
If p^.U=Nil Then Root:=p^.L {Удаляем корень}
Else {не корень}
If p^.U^.L=p Then p^.U^.L:=p^.L
Else p^.U^.R:=p^.L;
p^.L^.U:=p^.U;
End
Else Begin
{Есть и левый и правый потомки - сделаем шаг вправо, затем влево до упора; находим вершину pp}
pp:=p^.R;
While pp^.L<>Nil Do pp:=pp^.L;
p^.I:=pp^.I; {поменяем местами элементы p и pp;}
p:=pp; {удалим pp как не имеющего левого потомка.}
If p^.U^.L=p Then p^.U^.L:=p^.R
Else p^.U^.R:=p^.R;
If p^.R<>Nil Then p^.R^.U:=p^.U;
End;
Dispose(p);
End;
Наряду со сбалансированными бинарными деревьями в практических приложениях используют выровненные бинарные деревья. Выровненное дерево - это “почти строго” бинарное дерево. У него все уровни, кроме нижнего, заполнены; незаполненным может быть только нижний уровень, причем все “пустые места” расположены справа. Такая структура обеспечивает максимальную компактность дерева, то есть при данном количестве элементов дерево имеет минимально возможную высоту; кроме того, выровненное дерево очень удобно хранить в обычном одномерном массиве. Выровненное бинарное дерево, в котором элементы-предки всегда больше своих потомков, называется сортдеревом. Известны алгоритмы сложности не более log2(n), позволяющие добавлять элементы в сортдерево и удалять из него элементы. Пусть линейная проекция сортдерева, полученная обходом сверху вниз, записана в массиве S с индексами 1,2,3,... Элемент S[1] - это корень дерева, S[2] и S[3] - соответственно левый и правый потомки корня. S[4] и S[5] - левый и правый потомки S[2] и так далее. Легко понять, что индексы левого и правого потомка элемента S[p] всегда равны 2p и 2p+1, а индекс родителя элемента S[k] равен k Div 2. Это обстоятельство и позволяет не использовать древовидную структуру для хранения сортдерева.
Та же самая структура данных иногда описывается как приоритетная очередь. Приоритетной очередью называют такую последовательность элементов, из которой первым извлекается не элемент, записанный первым, как в обычной очереди, и не элемент, записанный последним, как в стеке, а элемент, имеющий наибольший приоритет. Будем считать, что из двух элементов больший приоритет имеет больший элемент, и условимся всегда извлекать из сортдерева только корневой элемент. Тогда оказывается, что сортдерево является одним из способов (конечно, не единственно возможным) организации приоритетной очереди. Поэтому алгоритмы, приведенные ниже, можно описывать как в терминах бинарного дерева, так и в терминах приоритетной очереди. Рассмотрим сначала алгоритм включения нового элемента. Запишем новый элемент в первую свободную позицию; если элемент больше своего родителя, то поменяем их местами и вновь проверим соотношение элемента и его нового родителя. Будем поступать так до тех пор, пока добавляемый элемент не станет меньше своего родителя или не окажется первым (корневым) элементом.
Procedure Add_SortTree(Var St : T_SortTree; Var n : Word; Ch : Char);
{St - линейная проекция сортдерева (одномерный массив), n - количество элементов в проекции, Ch - добавляемый элемент}
Var
k : Word;
tmp : Char;
Begin
Inc(n); {увеличили количество элементов на 1}
St[n]:=Ch; {записали элемент в "хвост"}
k:=n; {k - текущее положение нового элемента в проекции}
While (k>=2)And(St[k]>St[k Div 2]) Do Begin
{меняем местами родителя и потомка}
tmp:=St[k];
St[k]:=St[k Div 2];
St[k Div 2]:=tmp;
{вычисляем новое положение элемента}
k:=k Div 2;
End;
End;
Теперь запишем алгоритм удаления корневого элемента сортдерева. Удалим корневой элемент, заменив его большим из его потомков, на освободившееся место записываем большего из потомков и так далее до тех пор, пока потомков не окажется. Если последний перемещенный вверх элемент не является концевым элементом проекции, то образуется “дырка”, которую следует заполнить. “Дырка” заполняется следующим образом: перемещаем туда концевой элемент проекции; если он оказывается больше своего родителя, применяем алгоритм, аналогичный алгоритму включения нового элемента.
Procedure Del_SortTree(Var St : T_SortTree; Var n : Word);
Var
k,k1,k2,t : Word;
tmp : Char;
Begin
k:=1; {текущая позиция удаляемого элемента}
While 2*k<=n Do Begin {пока у элемента k есть потомки}
k1:=2*k; {левый потомок}
k2:=k1+1; {правый потомок}
t:=k1; {t - наибольший из них}
If (k2<=n)And(St[k2]>St[k1]) Then t:=k2;
St[k]:=St[t]; {заменяем элемент k} k:=t;
End;
If k<n Then Begin {получилась "дырка"}
St[k]:=St[n]; {заполняем ее концевым элементом}
While (k>=2)And(St[k]>St[k Div 2]) Do Begin
{перемещаем его в нужное место}
tmp:=St[k]; St[k]:=St[k Div 2]; St[k Div 2]:=tmp; End;
End;
Dec(n);
End;
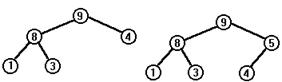
Пусть элементы включаются в сортдерево в такой последовательности: 4,1,8,9,3,5,2,7. Тогда сортдерево будет расти так, как показано на рисунке.
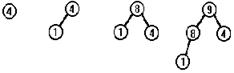
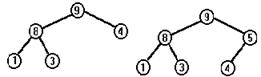
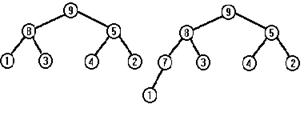
Будем последовательно удалять из этого дерева корневой элемент, пока дерево не станет пустым. Последовательные стадии уменьшения сортдерева показаны на следующем рисунке.