Скорости точек тела при плоскопараллельном движении

Теорема 1.Абсолютная скорость () любой точки плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости (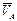) произвольно выбранного полюса в поступательном движении плоской фигуры и вращательной скорости (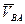) во вращательном движении фигуры относительно полюса.

 

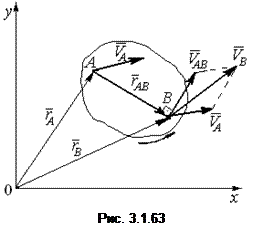
Положение любой точки В тела можно определить равенством (рис. 3.1.63)

.

Взяв производную от обеих частей уравнения по времени получим,

,

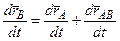где – искомая скорость;

– скорость полюса;

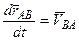– скорость точки В при вращательном движении тела вокруг полюса А при .

Таким образом

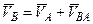, (3.1.75)

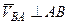, V_BA = ω AB.

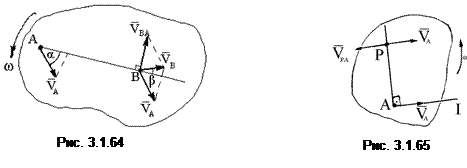
Теорема 2. Проекции скоростей двух точек плоской фигуры на ось, проходящую через эти точки, равны и имеют одинаковый знак (рис. 3.1.64). Зная, что 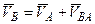, спроецируем данное выражение на прямую АВ, тогда

V_В cos β = V_А cosα. (3.1.76)

Теорема 3.Плоская фигура в каждый момент времени имеет одну точку, абсолютная скорость которой равна нулю. Эта точка называется мгновенным центром скоростей (МЦС), обозначим ее буквой Р (рис. 3.1.65). Докажем существование МЦС.

Пусть скорость V_А и ω заданы. Повернем полупрямую АI на 90° в сторону вращения плоской фигуры. Отложим отрезок АР = V_A/ω, тогда точка Р и будет искомой:

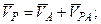V_PA = АР·ω =,

|.

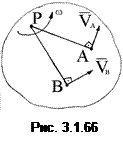При движении плоской фигуры положение МЦС непрерывно меняется. Графически МЦС находится, как точка пересечения перпендикуляров, восстановленных из двух точек к направлениям их скоростей (рис. 3.1.66):

V_A = PA·ω; ω = .

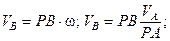
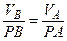Скорости точек плоской фигуры пропорциональны расстояниям от них до мгновенного центра скоростей.

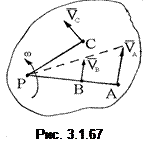Если за полюс выбран МЦС, то скорость любой точки плоской фигуры есть вращательная скорость вокруг МЦС. Модуль скорости пропорционален расстоянию от точки до МЦС (рис. 3.1.67).

Зная для данного момента времени положение МЦС и скорость какой-либо точки В плоской фигуры, можно определить угловую скорость и скорость любой точки плоской фигуры (рис. 3.1.68).

Если известны скорость одной точки А по модулю и направлению и направление скорости другой точки В, то можно определить скорости всех точек плоской фигуры (рис. 3.1.69). Для этого необходимо найти положение МЦС, проведя перпендикуляры к векторам скоростей V_A и V_B, затем определить ω по формуле

w = ,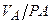

после чего найти скорости точек по формулам:

V_B = PB×w, V_C = PC ω.

Частные случаи определения положения МЦС. Известны направления скоростей двух точек. Рассмотрим этот случай на примере кривошипно-шатунного механизма (рис. 3.1.70). Направления скоростей точки А кривошипа и ползуна В известны. МЦС должен лежать в точке пересечения перпендикуляров к направлениям скоростей этих точек. Эта точка в бесконечности. Точка А принадлежит кривошипу и ее скорость V_А = OAω, но точка А также принадлежит и шатуну АВ. Выберем точку А за полюс, тогда , спроецируем на прямую АВ:

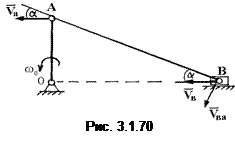V_В cos α = V_А cos α; |V_В| = |V_А|.

Спроецируем векторное равенство на перпендикуляр к АВ:

V_В sin α = V_А sin α + V_ВА Þ V_ВА = 0,

V_ВА = AB·ω_АВ Þ ω_АВ = 0.

Шатун АВ совершает мгновенно-поступательное движение.

Следовательно, если угловая скорость плоской фигуры равна нулю, то МЦС удален в бесконечность и тело совершает мгновенно-поступательное движение. Скорости всех точек плоской фигуры равны по величине и направлению.

Если скорости двух точек плоской фигуры параллельны между собой и перпендикулярны линии, соединяющей эти точки, то МЦС можно найти из условия пропорциональности скоростей точек расстояниям от этих точек до МЦС (рис. 3.1.71).

Рис. 3.1.71

При качении без скольжения одного тела по поверхности другого неподвижного тела МЦС совпадает с точкой соприкосновения тел, так как при отсутствии скольжения скорость точки соприкосновения равна нулю (рис. 3.1.72).

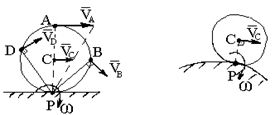
Рис. 3.1.72

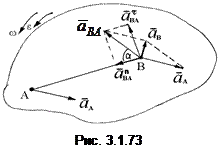
Определение ускорений точек тела. Абсолютное ускорение 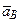любой точки В плоской фигуры равно геометрической сумме ускорения полюса А и ускорения точки В во вращательном движении фигуры вокруг полюса (рис. 3.1.73):

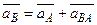. (3.1.77)

 

Движение плоской фигуры задано:

X_А = f₁(t); Y_A = f₂(t); φ = f₃(t);

V_A = , , .

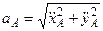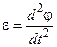Ускорение 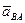точки В во вращательном движении вокруг полюса найдем по формулам (3.1.71) и (3.1.72):

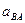= tg α =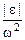

или

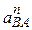= BA·ω² и = ВА·ε.

Вектор 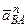всегда направлен от точки В к полюсу А, вектор направлен перпендикулярно ВА в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное.

Тогда вместо равенства (3.1.77) получим

. (3.1.78)

Пример.Центр колеса, катящегося по прямой, имеет в данный момент скорость V₀ = 1 м/с и ускорение 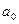= 2 м/с² . Радиус колеса (R) равен 0,2 м. Определите ускорение точки В – конца перпендикулярного ОР диаметра АВ и ускорение точки Р, совпадающей с мгновенным центром скоростей (рис. 3.1.74).

Решение. V₀ и 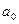известны, поэтому принимаем точку О за полюс. Определяем ω. Точка касания Р является мгновенным центром скоростей, следовательно,

ω =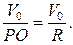

Так как величина РO = R остается постоянной при любом положении колеса, то, найдя производную от ω, получим

ε =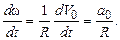

Знаки ω и ε совпадают, следовательно, вращение колеса ускоренное. Следует помнить, что ε определяется таким образом только в том случае, когда РO – величина постоянная.

Определяем 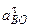и . Так как за полюс взята точка О, то

.

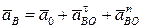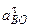= BО·ε; 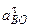= = 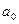2 м/с², = ВО·ω² = = 5 м/с².

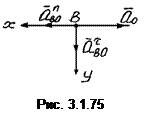Изобразим все ускорения, приложенные в точке В (рис. 3.1.75).

Проведя оси Вх и Вy, находим м/с², м/с², откуда м/с².

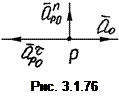Аналогично находится и ускорение точки Р (рис. 3.1.76):

, Р₀·ε = 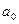=2 м/с², 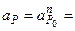5 м/с².

Ускорение точки Р, скорость которой в данный момент равна нулю, нулю не равно.

Тема 10. Сферическое движение твердого тела

Сферическое движение – движение твердого тела, одна из точек которого во все время движения остается неподвижной (например, движение волчка). Точки тела движутся по сферическим поверхностям. Положение тела определяют при помощи трех углов (рис. 3.1.77). Для этого задаются две системы координат: неподвижная Оxyz и подвижная ОxhV, связанная с твердым телом. Линия ОJ – линия узлов, задаются углы: Y – угол прецессии, q – угол нутации, j – угол собственного вращения – углы Эйлера. Таким образом, уравнения сферического движения выглядят следующим образом: Y = f₁(t); q = f₂(t); j = f₃(t). Углы отсчитываются от осей против хода часовой стрелки.

Теорема Эйлера-Даламбера: всякое перемещение тела, имеющего неподвижную точку, можно заменить одним поворотом вокруг некоторой мгновенной оси вращения, проходящей через эту точку (рис. 3.1.78). Скорости всех точек тела, лежащих на мгновенной оси вращения в данный момент времени равны нулю.

Вектор угловой скорости (мгновенной угловой скорости) откладывается от неподвижной точки по мгновенной оси вращения 1 в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение происходящим против часовой стрелки. Вектор угловой скорости со временем изменяется не только по численной величине, но и по направлению. Конец вектора описывает годограф 2 скорости вектора 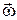. Угловое ускорение определяется по формуле

.

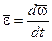Скорость конца вектора 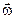, совпадает по направлению с касательной к годографу вектора угловой скорости. В случае сферического движения в отличие от случая вращения вокруг неподвижной оси вектор 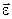не совпадает с направлением .

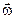Скорости точек при сферическом движении определяются по формуле

,

где 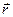– радиус-вектор точки, проведенный из неподвижной точки.

Модуль скорости находится по формуле

v = wr×sina; v = w×h,

где h – расстояние от точки до мгновенной оси вращения.

Формула Эйлера:

.

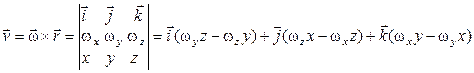Ускорения (рис. 3.1.79):

- полное ускорения: ;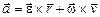

- вращательного ускорения: .

Модуль вращательного ускорения: а^вр = e×r×sinb; а^вр = e×h₁, где h₁ – расстояние от точки до вектора 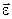, направлено перпендикулярно плоскости, проходящей через точку М и вектор ;

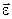- осестремительного ускорения: .

Модуль осестремительного ускорения:

а^ос= w²×h,

где h – направлено к оси вращения.

Движение свободного твердого тела (общий случай движения). Свободное твердое тело имеет шесть степеней свободы. При рассмотрении движения свободного твердого тела, кроме неподвижной системы координат Oxyz, вводится подвижная система координат Ax₁y₁z₁, которая связана с телом в точке А. Тогда движение свободного твердого тела представляет собой сложное движение, которое можно рассматривать как состоящее из поступательного движения вместе с полюсом (А) и сферическое движение вокруг полюса.

Уравнения движения свободного твердого тела:

x_A = f₁(t); y_A = f₂(t); z_A = f₃(t); Y = f₄(t); q = f₅(t); j = f₆(t).

Первые три уравнения определяют поступательную часть движения и зависят от выбора полюса, остальные три определяют сферическое движение вокруг полюса и от выбора полюса не зависят.

Скорость любой точки (М) свободного твердого тела равна геометрической сумме скорости полюса (А) и скорости этой точки в ее сферическом движении вокруг полюса (рис. 3.1.80):

.

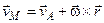Ускорение точки свободного твердого тела равно геометрической сумме ускорения полюса, осестремительного ускорения точки и ее вращательного ускорения, определенных относительно мгновенной оси и оси углового ускорения, проходящих через полюс:

.

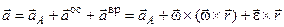Два последних члена дают ускорение точки в ее движении вокруг полюса.

Тема 11. Сложное движение точки

Относительное, переносное и абсолютное движения. Сложное движение точки – это такое движение, при котором точка одновременно участвует в двух или нескольких движениях. При определении движения ВС относительно земли приходится учитывать и движение воздушного потока, в котором оно перемещается.

Рассмотрим сложное движение точки М, перемещающейся по отношению к подвижной системе отсчета O₁x₁y₁z₁, которая, в свою очередь, как-то движется относительно другой системы отсчета Oxyz, условно считаемой неподвижной (рис. 3.1.81).

Движение точки М относительно подвижной системы отсчета O₁x₁y₁z₁ называют относительным движением точки. Скорость и ускорение точки в относительном движении называютотносительной скоростью () и относительным ускорением. Движение подвижной системы отсчета и неизменно связанного с ней тела по отношению к неподвижной системе отсчета Oxyz, называется переносным движением.

Переносной скоростью () ипереносным ускорением (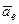) точки называется абсолютная скорость и ускорение той неизменно связанной с подвижными осями точки, с которой в данный момент совпадает точка М.

Движение точки М относительно неподвижной системы отсчета Oxyz называется абсолютным или сложным движением. Скорость и ускорение точки в абсолютном движении называют абсолютной скоростью(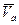) и абсолютным ускорением ().

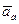Теорема о сложении скоростей. Для установления связи между скоростями точки в двух системах отсчета воспользуемся следующими векторными равенствами (см. рис. 3.1.81):

; (3.1.79)

; (3.1.80)

, (3.1.81)

Поскольку при определении относительной скорости можно «забыть» о переносном движении, т.е. считать оси о₁х₁у₁z₁ неподвижными, продифференцировав равенство (3.1.80) в этом предположении, найдем

. (3.1.82)

Таким образом, относительная скорость точки в сложном движении определяется обычными методами кинематики точки для неподвижных систем координат.

При определении переносной скорости исключаем относительное движение, т.е. полагаем || = const. Продифференцировав векторное равенство (3.1.80) в этом предположении, найдем

.

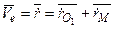Учитывая, что = 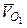– скорость начала подвижной системы координат, а 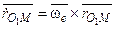, где ω_е – угловая скорость переносного движения системы, окончательно получаем

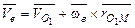. (3.1.83)

Формула (3.1.83) определяет вектор переносной скорости точки в общем случае свободного переносного движения. В частных случаях переносного движения формула (3.1.83) упрощается, например, при поступательном переносном движении ω_e = 0, а при вращательном переносном 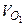= 0.

Абсолютную скорость точки найдем, продифференцировав по времени векторное равенство (3.1.81):

.

Учитывая, что 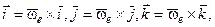а также равенства (3.1.82) и (3.1.83), получаем

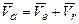. (3.1.84)

Формула (3.1.84) представляет собой математическую запись теоремы о сложении скоростей в сложном движении: абсолютная скорость точки равна геометрической сумме ее переносной и относительной скоростей.

Модуль определяем по теореме косинусов:

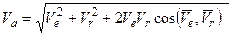. (3.1.85)

Следует отметить, что в самолетовождении теорема о сложении скоростей применяется в следующей интерпретации: путевая скорость самолета равна геометрической сумме скорости воздуха 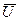и воздушной скорости самолета :

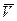. (3.1.86)

Теорема о сложении ускорений. Абсолютное ускорение, характеризующее изменение абсолютной скорости в абсолютном движении, найдем, продифференцировав по времени векторное равенство (3.1.84):

.

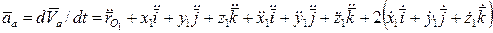1 группа – производные только от векторов ;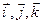

2 группа – производные только от относительных координат;

3 группа – производные от векторов и относительных координат.

Каждая из групп соответствует некоторому ускорению. Переносное ускорение 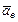– вычисляется, как если бы точка М покоилась по отношению подвижной системы осей (x₁, y₁, z₁ = const) и перемещалась вместе с ними по отношению к неподвижной системе; 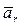– вычисляется, как если бы координаты x₁, y₁, z₁ менялись, а векторы были постоянны.

Последнее слагаемое называют поворотным ускорением, или ускорением Кориолиса – по имени французского ученого Г. Кориолиса (1792 – 1843) Поворотное ускорение определяется по формуле

.

Используя формулы Пуассона, получаем

; ; ,

тогда

;

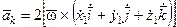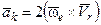. (3.1.87)

Формула абсолютного ускорения точки в сложном движении принимает следующий вид:

. (3.1.88)

Абсолютное ускорение точки в сложном движении равно геометрической сумме ее переносного, относительного и поворотного ускорений.

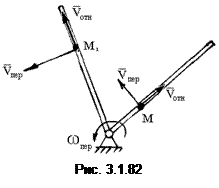Модуль и направление ускорения Кориолиса. Поворотное ускорение характеризует одновременно и изменение вектора переносной скорости в относительном движении, и изменение вектора относительной скорости в переносном движении (рис. 3.1.82).

Модуль поворотного ускорения, как это следует из определения векторного произведения,

. (3.1.89)

Поворотное ускорение может быть равно нулю в трех случаях: или , или V_r = 0, или относительная скорость параллельна оси переносного вращения (например, точка перемещается по образующей цилиндра, вращающегося вокруг оси своей симметрии).

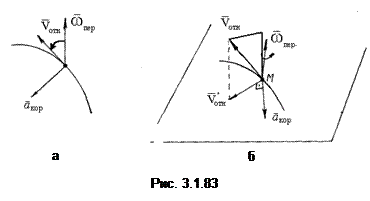
Для определения направления поворотного ускорения используется или обычное правило векторного произведения, или правило Н.Е. Жуковского. Рассмотрим оба этих правила. Как известно, вектор векторного произведения 2(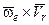) перпендикулярен плоскости перемножаемых векторов и направлен в ту сторону, откуда поворот первого вектора в произведении ко второму на наименьший угол виден против движения часовой стрелки (рис. 3.1.83, а).

Согласно правилу Н.Е. Жуковского (рис. 3.1.83, б), чтобы найти направление поворотного ускорения, нужно спроецировать относительную скорость точки на плоскость, перпендикулярную оси переносного вращения , и повернуть эту проекцию в той же плоскости на 90° в сторону переносного вращения (см. рис. 3.1.83, б).

Пример.Самолет, пролетающий над пунктами А и B (рис. 3.1.84), имеет воздушную скорость , равную по модулю 550 км/ч; вектор скорости ветра составляет с направлением AB угол γ = 150° (угол ветра). Найдите угол сноса (α) и время перелета, если скорость ветра равна 20 м/с и расстояние AB составляет 800 км.

Решение. В треугольнике скоростей (рис. 3.1.84, б) – скорость самолета относительно воздуха, – скорость ветра и – абсолютная (путевая скорость), направление которой совпадает с AB.

По теореме синусов

,

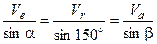откуда

.

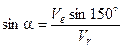Подставив в уравнение значение скорости ветра

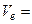20·3,6 = 72 км/ч,

получим

α = 3°45′.

Найдем третий угол треугольника:

β = 180° – 150° – 3°45′ = 26°15′.

Тогда

V_а = 486 км/ч.

Время перелета

t = ; t = 1 ч 39 мин.