Завдання на роботу

1. Погодити з викладачем завдання щодо типу і параметрів досліджуваних динамічних ланок.

2. За допомогою пакету Simulink побудувати реакцію кожної типової ланки (див. таблицю 1.1) на ступінчастий вхідний сигнал.

3. Визначити вплив коефіцієнтів, що входять в опис кожної ланки на параметри перехідного процесу.

4. Обчислити та побудувати амплітудно-фазо-частотні (АФЧХ) характеристики заданих динамічних ланок за допомогою пакету MATLAB.

 

1.1 . Стислі теоретичні відомості

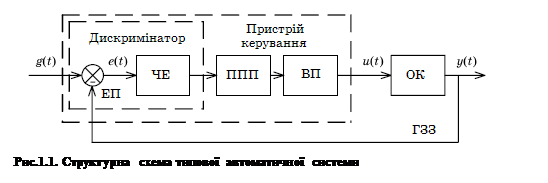Більшість автоматичних систем складаються з деяких типових за призначенням пристроїв або функціональних елементів, сукупність яких приведена в загальному вигляді на рис.1.1. До числа цих елементів входять: елемент порівняння ЕП, чутливий елемент ЧЕ, підсилювально-перетворюючий пристрій УПУ, виконавчий пристрій ВП і об'єкт керування ОК. Елемент порівняння разом з чутливим елементом утворює дискримінатор, а весь ланцюжок показаних послідовно сполучених ланок (окрім об’єкту керування) – пристрій керування. Наявність петлі головного зворотного зв’язку ГЗЗ означає, що представлена система є замкненою.

Елементи автоматичних систем характеризуються за їх призначенням, принципом дії, конструкцією, електричною схемою, тощо. Кожен з цих елементів має вхід та вихід і описується математичними виразами, що пов’язують його вихідну величину з вхідною. Даний математичний зв’язок визначає тип ланки, до якої відноситься окремий досліджуваний елемент. При цьому розрізняють два випадки:

– залежність вихідної величини елементу від вхідної відповідає сталому режиму;

– залежність вихідної величини елементу від вхідної відповідає несталому (перехідному) режиму.

У першому випадку залежність “вихід-вхід” є статична характеристика, в другому – динамічна характеристика.

Статична характеристика елементу описується алгебраїчними рівняннями. По вигляду статичної характеристики елементи автоматичних систем поділяються на дві групи – лінійні ланки і нелінійні ланки.

Статична характеристика нелінійної ланки в загальному випадку має наступний вигляд: x₂ = F(x₁), де F(…) – деяка нелінійна функція свого аргументу. Важливим є те, що статичні характеристики ланок замкнених автоматичних систем є непарними функціями, тобто . Це означає, що зі зміною знаку вхідної величини змінюється знак його вихідної величини, що принципово необхідне для функціонування замкнених автоматичних систем. За наявності навіть невеликої асиметрії в характеристиці одного з елементів виникає похибка автоматичної системи у вигляді зміщення керованої величини у(t) відносно задаючої дії g(t).

Динамічна характеристика ланки автоматичної системи визначається диференціальним рівнянням, яке відображає динамічні процеси в ній. Слід сказати, що різні за фізичними принципами дії елементи часто описуються однаковими диференціальними рівняннями, тому їх відносять до однієї групи динамічних ланок.

Під динамічною ланкою розуміється пристрій будь-якого фізичного вигляду і конструкції, що описується певними диференціальними рівняннями.

Класифікація ланок автоматичних систем проводиться саме за виглядом диференціального рівняння. Одні і ті ж рівняння можуть описувати найрізноманітніші пристрої (механічні, гідравлічні, пневматичні, електричні, тощо). Для теорії автоматичного керування це буде один і той самий тип ланки.

Позначивши вхідну величину ланки (рис.1.2) через x₁, а вихідну – через x₂, проведемо класифікацію ланок по вигляду їх реакції на вхідну дію.

У ланках позиційного, або статичного типу в усталеному режимі вхідна і вихідна величини зв’язані лінійною залежністю x₂ = kx₁ (рис.1.3, а). Коефіцієнт пропорційності k між вхідною і вихідною величинами є коефіцієнтом підсилення ланки.

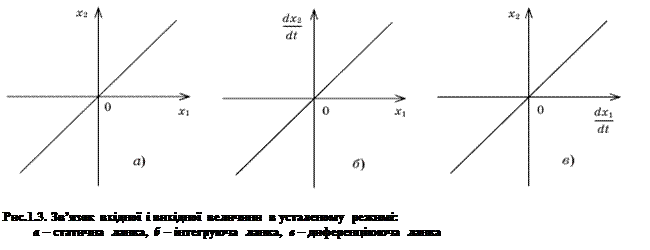
У ланках інтегруючого типу в усталеному режимі лінійною залежністю зв’язані похідна вихідної величини і вхідна величина (рис.1.3, б). В цьому випадку для усталеного режиму буде справедливим вираз , звідки і пішла назва цього типу ланок. Коефіцієнт пропорційності k в цьому випадку також є коефіцієнтом підсилення ланки. Якщо вхідна і вихідна величини ланки мають однакову розмірність, то коефіцієнту підсилення відпо

 

 

відає розмірність, с^–1.

У ланках диференціюючого типу лінійною залежністю 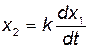зв’язані в усталеному режимі вихідна величина і похідна вхідної (рис.1.3, в), звідки і пішла назва цього типу ланок. Коефіцієнт пропорційності k є коефіцієнтом підсилення ланки. Якщо вхідна і вихідна величини ланки мають однакову розмірність, то коефіцієнту підсилення відповідає розмірність, с.

Класифікація ланок проводиться за виглядом диференціального рівняння або, що те ж саме, за виглядом передавальної функції ланки.

Під типовими динамічними ланками розуміють ті, які описуються диференціальними рівняннями не вище другого порядку:

.

Якщо ввести оператор диференціювання 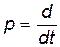, то можна записати в операторній формі:

,

звідки одержуємо

,

де 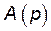і 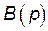– поліноми із формули .

Вираз по вигляду співпадає з визначенням передавальної функції як відношення перетворення по Лапласу вихідної змінної до перетворення по Лапласу вхідної змінної при нульових початкових умовах.

Відзначимо, що . Це означає, що коефіцієнт k є коефіцієнтом підсилення при нульовій частоті («постійному струмі»).

Комплексні числа, що є коренями многочлена B(p), називаються нулями передавальної функції, а корені многочлена A(p) – полюсами.

Опис типових динамічних ланок приведений в таблиці 1.1.

Таблиця 1.1. Типові динамічні ланки
№	Назва ланки	Реакція ланки на вхідну дію	Передавальна функція ланки
	Інтегруюча	Інтегруюча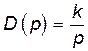
	Диференціюючи	Диференціююча	D(p) = kp
	Підсилююча (безінерційна)	Статична	D(p) = k
	Аперіодична 1-го порядку (інерційна)	Статична
	Аперіодична 2-го порядку (всі корені дійсні)	Статична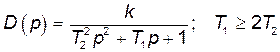
	Коливальна	Статична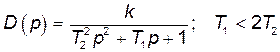
	Консервативна	Статична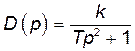
	Інтегруюча з запізненням (реальна інтегруюча)	Інтегруюча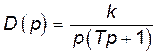
	Диференціююча з запізненням (реальна диференціююча)	Диференціююча
	Форсуюча	Диференціююча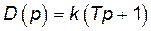
	Ізодромна	Інтегруюча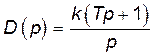
	Стабілізуюча	Диференціююча

Часові характеристики динамічної ланки є залежністю вихідного сигналу системи від часу при подачі на її вхід деякого типового впливу. Зазвичай виконується аналіз виходу системи на одиничний стрибок (функція Хевісайда).

Одиничний стрибок 1(t) визначається умовами:

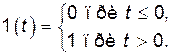
Реакція системи автоматичного керування на одиничний стрибок називається перехідною функцією системи і позначається h(t). При неодиничній ступінчастій дії g(t) = N1(t), де N = const, відповідно до принципу суперпозиції вихідна реакція системи буде у(t) = Nh(t).

Найважливішим поняттям, широко вживаним в ТАК, є поняття частотних характеристик. Саме методи, засновані на застосуванні частотних характеристик, є найбільш конструктивними і зручними в інженерній практиці. Вони найбільш застосовні в класичному випадку системи з одним входом і виходом.

Амплітудно-фазо-частотною характеристикою (АФЧХ) блоку з передавальною функцією D(p) називається комплексна функція дійсного аргументу , яка отримана при підстановці .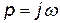

Підстановка 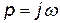в зображення по Лапласу довільної функції (оригіналу) перетворює перетворення Лапласа на спектр або, що є те ж саме, в перетворення Фур’є. Тому від передавальної функції переходимо до спектрів вхідного і вихідного сигналів.

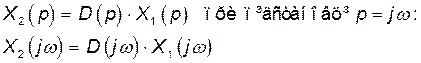
описує зміну спектру при проходженні через блок з передавальною функцією D(p). Формула справедлива для будь-якого вхідного сигналу. АФЧХ описується наступною формулою:

де 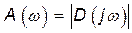– АЧХ – Амплітудно-частотна характеристика;

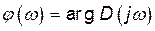– ФЧХ – Фазо-частотна характеристика.

Частотні характеристики показують амплітуду і фазу сталого гармонійного сигналу на виході під час подачі на вхід гармонійного сигналу одиничної амплітуди.

АФЧХ зручно зображати у вигляді годографа на комплексній площині з координатами 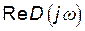і (рис.1.4).

Параметром на 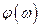кривій годографа є частота, що змінюється в інтервалі від 0 до 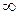. Для довільної частоти 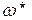радіус вектор в точці показує амплітуду вихідного сигналу, а кут 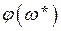– зсув фази між вихідним і вхідним сигналом. Іноді ще називають комплексним коефіцієнтом передачі, маючи на увазі те, що АФЧХ є узагальненням звичайного коефіцієнта підсилення k на випадок його залежності від частоти і наявний фазовий зсув, який також залежить від частоти.

1.2. Методичні вказівки

1. Необхідно розглянути всі типові динамічні ланки, що приведені в табл.1.1. Параметри вказаних ланок обираються згідно номера N індивідуального варіанту (див. таблицю 1.2), який видається викладачем.

Таблиця 1.2. Параметри типових динамічних ланок
Номер ланки по табл.1.1	Передавальна функція ланки	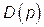Коефіцієнт підсилення k	Постійна часу T1, c	Постійна часу T2, c
			–	–
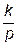
	Kp		–	–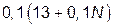
	K		–	–
				–
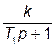
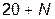
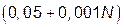
Продовження табл.... 1.2
				–
				–
				–
			–
				–
		–	–

 

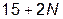
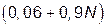
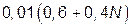
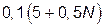
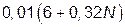
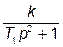
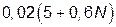
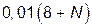
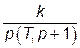
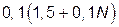
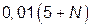
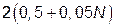
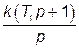
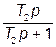
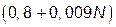
2. Реакцію кожної типової ланки (див. табл. 1.1) на ступінчасту вхідну дію (функцію Хевісайда) за допомогою пакету Simulink можна наступним чином:

· запустити програмний пакет Simulink (див. стор. 4-5);

· створити нову модель (див. меню File, або натиснувши Ctrl+N);

· перетягнути блок Transfer fun, що знаходиться в підрозділі Continuous головної бібліотеки Simulink. Задати необхідні параметри ланки (див. табл. 1.2);

· для подачі типових впливів потрібно використати блок Step з підрозділу Sources. При цьому величина Final value дорівнює номеру варіанту N.

· за допомогою блоку Scope з підрозділу Sinks зафіксувати вихідний сигнал ланки.

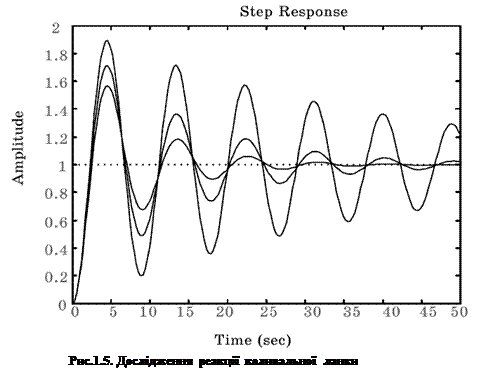
3. Для трьох різних комбінацій значень коефіцієнту підсилення k і постійних часу T₁ і T₂, що обираються довільно розрахувати перехідний процес для аперіодичної ланки (№4 в табл. 1.1) і коливальної ланки (№6 в табл. 1.1). Одержані перехідні характеристики представити для кожної ланки окремо на одному графіку.

На рис.1.5 показаний приклад моделювання динаміки коливальної ланки при різних параметрах коефіцієнту підсилення і постійних часу.

4. В пакеті Matlab необхідно обчислити і побудувати амплітудно-фазо-частотну характеристику кожної типової динамічної ланки (див. табл. 1.1) із заданими в табл. 1.2 параметрами згідно індивідуального варіанту.

Алгоритм розрахунку АФЧХ розглянемо на прикладі передавальної функції, яка має наступний вигляд:

,

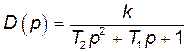де , , .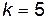

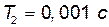1) Замінюємо в передавальній функції оператор p на :

,

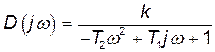2) задаємо в командному рядку системи Matlab (Command Window) параметри ланки та діапазон зміни частоти
>> k=5; T1=0.02; T2=0.001;
>> w=0:1:10000;

3) розраховуємо уявну величину
>> jw=i*w;

4) розраховуємо передавальну функцію
>> D=k./(-T2*w.^2+T1*jw+1);

5) обчислюємо амплітуду 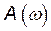і фазу вихідного сигналу
>> A=abs(D); F=angle(D);

6)

будуємо графік АФЧХ
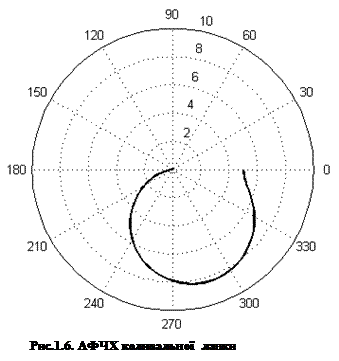
>> polar(F, A)

На рис.1.6 представлений графік розрахованої АФЧХ.

Зміст протоколу

1. Титульний лист.

2. Мета роботи.

3. Опис лабораторної роботи, в якому обов’язково повинні бути відображені постановка задачі, диференціальні рівняння і передавальні функції досліджуваних динамічних ланок.

4. Результати роботи у вигляді роздруків лістингів програми розрахунку амплітудно-фазо-частотних характеристик, а також перехідних характеристик окремих динамічних ланок.

5. Висновки по роботі.

 

Контрольні запитання

1. Визначення передавальної функції та перехідної характеристики. Класифікація динамічних ланок.

2. Зв’язок диференціального рівняння автоматичної системи і її частотної передавальної функції.

3. Поняття комплексної частотної передавальної функції, амплітудно-частотної, фазо-частотної і амплітудно-фазової характеристик.

4. Методика розрахунку і графічного представлення частотних характеристик в програмі Matlab.

5. Типові динамічні ланки. Визначення і класифікація.

6. Диференціальні рівняння, частотні передавальні функції, перехідні окремої групи типових динамічних ланок (уточнюється викладачем).