Моделей
2.1. Условные математические ожидания.
Не каждый ЭО может быть описан рассмотренными в главе 1 динамическими моделями. Часто возникают ситуации, когда по имеющейся информации (данным), например, совокупности X некоторого компонента вектора S состояния ЭО, требуется предсказать (оценить) некоторую величину Y, стохастически связанную с X. Стохастическая связь означает, что X и Y имеют некоторое совместное распределение Pr(X, Y). Причем, непосредственно величину Y измерить невозможно. Например, совокупность X может быть образована временным рядом S1, S2, … , st динамической переменной ЭО, а Y = St+T . Следовательно, есть величины, доступные измерению в некотором интервале времени, а прогнозу подлежат величины, связанные с будущим, невозможным наблюдению. Аналогичная ситуация встречается при многофакторном анализе, когда необходимо восстановить статистическую связь некоторого ненаблюдаемого параметра Y ЭО с N наблюдаемыми факторами X1, X2, … , XN .
В общем случае совокупность X: {X1, X2, …} некоторых случайных наблюдаемых величин называется предсказывающими или прогнозными переменными. Задача заключается в построении такой функции f(X) от этих величин, которую можно было бы использовать в качестве оценки для прогнозируемой величины Y. Функция f(X) должна быть «близка» по некоторой мере сравнения (сходства) к величине Y, т.е. Y @ f(X). Такие функции f(X) называют предикторами величины Y.
В главе 1 был рассмотрен частный случай построения (синтеза) предикторов, когда была известна некоторая динамическая связь между прогнозными переменными. Когда такая дополнительная информация отсутствует, остается прибегнуть лишь к теории уловных математических ожиданий.
Совместное распределение Pr(X, Y) двух случайных величин X и Y подчиняется закону
Pr(x, y) = Pr(x) Pr(yú x) = Pr(y) Pr(xú y), (2.1.1)
где Pr(yú x) – условное распределение случайной величины Y (распределение Y при условии, что X = x); Pr(xú y) – условное распределение случайной величины X; Pr(x) = ò Pr(x, y) dy – маргинальное распределение случайной величины X; Pr(y) = = ò Pr(x, y) dx – маргинальное распределение случайной величины Y.
В качестве распределений Pr обычно рассматриваются плотности вероятности для абсолютно непрерывных величин и вероятности для дискретных. Для дискретных величин при вычислениях знак интеграла заменяется знаком суммы, т.е. ò Þ å .
Из (2.1.1)следует, что
Pr(xú y) = Pr(x, y) / Pr(y), Pr(yú x) = Pr(x, y) / Pr(x). (2.1.2)
Условное «матожидание» случайной величины Y
rY(x) = ò y Pr(yú x) dy = ò y Pr(x, y) dy / Pr(x) =
= ò y Pr(x, y) dy /ò Pr(x, y) dy (2.1.3)
называется функцией регрессии Y на X.
Условной дисперсией случайной величины Y называется
DY(x) = ò [y – rY(x)]2 Pr(yú x) dy =
= ò [y – rY(x)]2 Pr(x, y) dy /ò Pr(x, y) dy. (2.1.4)
Поскольку rY(x) и DY(x) являются случайными величинами, зависящими от x, то можно вычислить полные (безусловные) математическое ожидания и дисперсию случайной величины Y
áYñ = árY(x)ñ, (2.1.5)
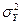 = D(y) = áDY(x)ñ = D(r) + D(yú x) =
= D(y) = áDY(x)ñ = D(r) + D(yú x) =  +
+  .
.
где усреднение á ñ производится по случайной величине X. Выражение (2.1.5) следует из правила расчета дисперсий (см. Модуль 1, стр. 57 главы 2).
Выражение (2.1.5) показывает, что полная ошибка определения случайной величины Y складывается из ошибки определения регрессии r (среднего значения Y при фиксированном значении случайной величины X) и ошибки определения статистической связи между Y и X.
Важное следствие из (2.1.5) заключается в том, что
 = D (r) £ D(y) =
= D (r) £ D(y) = 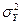 , (2.1.6)
, (2.1.6)
причем знак равенства выполняется лишь в случае, если
 = D(yú x) = á[y – rY(x)]2ñ = 0, т.е.
= D(yú x) = á[y – rY(x)]2ñ = 0, т.е.
y = rY(x) = ò y Pr(x, y) dy /ò Pr(x, y) dy . (2.1.7)
Это означает, что ошибка определения статистической связи между случайными величинами Y и X отсутствует. Статистическая связь полностью определяется регрессионной зависимостью (2.1.7).
Заметим, что подобно тому, как среднее (математическое ожидание) является важнейшей характеристикой распределения, регрессия является важнейшей характеристикой условного распределения.
Пример 2.1.1. Пусть совместное распределение случайных величин X и Y описывается нормальной плотностью вероятностей с áxñ, áyñ, D(x) = sX2 = áx2ñ, D(y) = sY2 = áy2ñ, cor(x, y) = rXY , ½rXY ½< 1. Тогда
Pr(x, y)=N(áxñ,áyñ;COVXY), Pr(yú x)=N(r(x);(1-rXY2)sY2), (2.1.8)
где
COVXY = 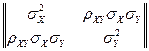 ,
,
COV-1XY = 
или
Pr(x, y) = exp{– [(x – áxñ)2/sX2 – 2rXY (x – áxñ)(y – áyñ)/sX sY +
+ (y – áyñ)2/sY2]/2(1 – rXY2)}/ 2p sX sY (1 – rXY2)1/2,
Pr(yú x) = Pr(x, y) / Pr(x) = (2.1.9)
= exp{– [(y – r(x)]2/2sY2 (1–rXY2)}/ (2p)1/2 sY (1 – rXY2)1/2.
При этом
r(x) = áyñ + (sY /sX) rXY (x – áxñ), (2.1.10)
 = sY2rXY2,
= sY2rXY2,  = sY2 (1 – rXY2).
= sY2 (1 – rXY2).
Тем самым, при нормальном совместном законе распределения случайных величин X и Y регрессия является линейной.
2.2. Оптимальный стохастический прогноз.
Оптимальный стохастический прогноз или оптимальный предиктор случайной величины X в классе всех функций y = f(x) по мере среднеквадратической ошибки (СКО) совпадает с функцией регрессии Y на X.
Действительно, будем искать функцию f(x) предиктора, воспользовавшись МНК, т.е. минимизируя СКО
СКО = ò [y – f(x)]2 Pr(yú x) dy . (2.2.1)
Тогда, записывая условия минимума СКО – ¶ СКО/¶f = 0, получим
¶ СКО/¶ f = ò [y – f(x)] Pr(yú x) dy = 0 .
Отсюда следует
f(x) ò Pr(yú x) dy = ò y Pr(yú x) dy.
Однако, т.к. òPr(yú x)dy = òPr(x, y)dy /Pr(x) = Pr(x)/Pr(x) = 1, то получим
f(x) = ò y Pr(yú x) dy = ò y Pr(x, y) dy /ò Pr(x, y) dy, (2.2.2)
что совпадает с (2.1.3), т.е. f(x) = rY(x).
Минимальная ошибка предсказания СКОмин может быть записана в соответствии с (2.2.1) в виде
СКОмин =  =ò [y – rY(x)]2 Pr(x, y) dy /ò Pr(x, y) dy. (2.2.3)
=ò [y – rY(x)]2 Pr(x, y) dy /ò Pr(x, y) dy. (2.2.3)
Для произвольного предиктора f(x)
cov(f,Y) = cov(f, rY(x)), (2.2.4)
cov(rY(x),Y) = cov(rY(x), rY(x)) = 
Тогда коэффициент корреляции
r2(f,Y) = cov2(f,Y) /sf2sY2 = {cov2(f, rY(x))/sf2sR2}sR2/sY2 =
= r2(f, rY(x)) r2(rY(x),Y) . (2.2.5)
Из (2.2.5) следует, что оптимальный предиктор rY(x) имеет максимальный коэффициент корреляции с Y среди всех возможных предикторов, т.е. r2(rY(x),Y) ≥ r2(f,Y) для любого f(x), т.к. r2(f, rY(x)) ≤ 1.
Квадрат максимального значения коэффициента корреляции r2(rY(x),Y) имеет специальное обозначение h2YX и называется корреляционным отношением. Из (2.1.5), (2.2.4) и (2.2.5) следует, что
hYX2 = sR2/ sY2 = 1 –  /sY2 = 1 – СКОмин /sY2 . (2.2.6)
/sY2 = 1 – СКОмин /sY2 . (2.2.6)
Отсюда следует, что hYX2 ® 1, если минимальная ошибка прогноза СКОмин ® 0. Тем самым, корреляционное отношение hYX2 представляет собой некую меру зависимости (или меру точности прогноза) между случайными величинами Y и X.
В случае нормальной корреляции (2.1.9) наилучший прогноз и его СКОмин =  имеют вид (2.1.10), а корреляционное отношение
имеют вид (2.1.10), а корреляционное отношение
h2YX = rXY2. (2.2.7)
Поскольку при нормальной корреляции наилучший прогноз (2.1.10) имеет линейную зависимость, то в случае общей зависимости разность h2YX – rXY2 может служить показателем отклонения регрессионной зависимости от линейной зависимости.
Так как h2YX ≥ rXY2 , то показатель отклонения регрессии от линейности всегда больше нуля.
Пример 2.2.1. Обобщим прогноз при нормальном распределении на многомерный случай. Пусть X = {x1, x2, … xn-1}, Y = = xn , n ³ 2 и Pr(Y, X) = N(áx1ñ, áx2ñ, … , áxnñ; COV), где COV = =½½skm½½n =½½á(xk – áxkñ) (xm – áxm)ñ½½n – невырожденная ковариационная матрица, имеющая обратную матрицу COV –1 = = ½½s km½½n.
В этом случае
Pr(YêX = x) = N(r(x1, x2, … , xn-1); 1/s nn), (2.2.8)
r(x1, x2, … , xn-1) = áxnñ – 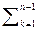 (xk – áxkñ) s kn /s nn ,
(xk – áxkñ) s kn /s nn ,
sYX2 = 1/s nn, sR2 = snn – 1/s nn,
hYX2 = 1 – 1/(snn s nn).
2.3. Синтез предикторов.
Синтез линейного предиктора.
Пусть предиктор описывается функцией множественной линейной регрессии
Y = b0 + b1 X1 + b2 X2 + … bp X p = b0 + b + X. (2.3.1)
В (2.4.1) введены векторные обозначения: b + = (b1, b2, …, bp) – вектор-строка (транспонированный вектор-столбец b); X – вектор-столбец
b + X = êb1, b2, …, bp ê = b0 + b1 X1 + b2 X2 + … bp X p.
= b0 + b1 X1 + b2 X2 + … bp X p.
(2.3.2)
Обозначим
COV+(Y,X) = {cov(Y,X1), cov(Y,X2), …, cov(Y,Xp)}, (2.3.3)
å = 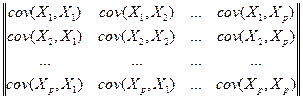 .
.
Тогда коэффициенты предиктора, минимизирующие ошибку (2.2.1) предсказания (см. также стр. 8), можно выразить в виде
b0 = áYñ – b + áXñ, (2.3.4)
b = å -1 COV(Y,X),
где å -1 – матрица, обратная к ковариационной матрице å .
Ошибка предиктора (2.2.1) определяется соотношением
СКОмин =  = sY2 – COV+(Y,X) å -1 COV+(Y,X). (2.3.5)
= sY2 – COV+(Y,X) å -1 COV+(Y,X). (2.3.5)
Корреляционное отношение (2.2.6)
hYX2 = COV+(Y,X) å -1 COV+(Y,X) / sY2 (2.3.6)
называется множественным коэффициентом корреляции.
Пример 2.3.1. Пусть предиктор описывается функцией множественной линейной регрессии Y = b0 + b1 X1 + b2 X2. Требуется провести оценку его коэффициентов b0 , b1, b2 и ошибку предсказания.
Решение. Ковариационная матрица å в соответствии с (2.3.3) выражается как
å =  . (2.3.7)
. (2.3.7)
Тогда,
å -1 =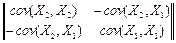 / Detå = (2.3.8)
/ Detå = (2.3.8)
= 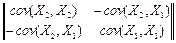 /
/
/[cov(X1, X1) cov(X1, X1) – cov2(X1, X2)].
Следовательно, в соответствии с (2.3.4)
b = å -1 COV(Y,X) = (2.3.9)
=  =
= 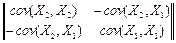
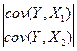 / Detå.
/ Detå.
Следовательно, коэффициенты предиктора и точность предсказания определяются выражениями
b1 = 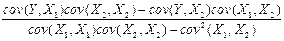 , (2.3.10)
, (2.3.10)
b2 =  ,
,
b0 = áYñ – b1áX1ñ – b2áX2ñ,
hYX2 = [b1 cov(Y, X1) + b2 cov(Y, X2)] / sY2 .
Для частного случая статистически независимых (ортогональных) переменных X1 и X2 , для которых cov(X1, X2) = 0, получим
b1 = 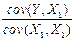 = cov(Y, X1) /sX12, (2.3.11)
= cov(Y, X1) /sX12, (2.3.11)
b2 = 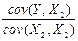 = cov(Y, X1) /sX22,
= cov(Y, X1) /sX22,
b0 = áYñ – 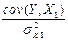 áX1ñ –
áX1ñ – 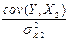 áX2ñ,
áX2ñ,
hYX2 = [ +
+  ] / sY2 .
] / sY2 .
Синтез нелинейного предиктора
для экспертного оценивания.
Предположим, что ЭО зависит от многомерного вектора структурных параметров (факторов) P = (P1, P2, …, PN). Пусть известны M эталонных состояний ЭО (M < N) с соответствующими векторами Pm = (Pm1, Pm2, …, PmN) (m = 1, 2, …, M). Пусть также в каждом эталонном состоянии ЭО известны значения Ym некоторого параметра Y состояния ЭО. Необходимо синтезировать регрессионную оценку параметра Y ЭО для произвольного значения P.
Если предположить, что структурные параметры статистически независимы (cov(Pk, Pn) = 0 для k ¹ n), то в соответствии с примером 2.3.1 получим линейную регрессионную оценку
Y = rлин(P) =  , (2.3.12)
, (2.3.12)
где
áYñ = 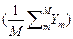 , áPnñ =
, áPnñ =  , (2.3.13)
, (2.3.13)
 ,
,
 .
.
Возможен другой подход с использованием нелинейного предиктора. Для этого введем M функций, представляющих собой меры сходства Xm = X(P, Pm) неизвестного P эталонного Pm векторов (m = 1, 2, …, M). Выберем функции такими, что cov(Xk, Xm) @ 0, Xkm = X(Pk, Pm) @ 0 для k ¹ m и Xkk = X(Pk, Pk) = 1. Такими функциями могут быть следующие нечеткие функции, рассмотренные в Модуле 1 (стр. 63, глава 2)
1) X(P, Pm) = exp{– a [exp(–½P – Pm ½2/2b 2) – 1]2}, (2.3.14)
2) X(P, Pm) = a /{a + [1 – exp(–½P – Pm ½2/2b 2)]N},
3) X(P, Pm) = a / {a +[åNn=1 (Pn – Pmn)2] N / (2b 2) N }.
Будем синтезировать нелинейный (по переменной P) предиктор в виде регрессии
Y = rнелин(P) = 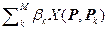 . (2.3.15)
. (2.3.15)
Опираясь на предыдущие результаты и учитывая, что X(Pk, Pm) < < X(Pm, Pm), получим
Y = rнелин(P) = 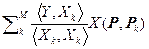 , (2.3.16)
, (2.3.16)
 @
@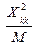 ,
,
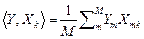 @
@ .
.
Тогда c учетом (2.3.14) регрессия (2.3.15) принимает вид
Y = rнелин(P) @ =
= . (2.3.17)
. (2.3.17)
СКО @
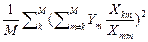 ≤
≤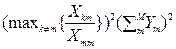 .
.
Если в качестве функций X(P, Pk) использовать нормированные «ядерные» оценки x(P, Pk) = X(P, Pk) / åkMX(P, Pk) условной плотности распределения Y, то (2.3.17) будет ядерной выборочной оценкой нелинейной регрессии (2.1.3)
Y = 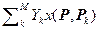 =
= /
/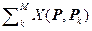 .
.
(2.3.18)