Обработка статистических данных и анализ случайных дискретных данных
Процедуру обработки дискретных выборочных данных можно проиллюстрировать на конкретном примере. Предположим, что мы анализируем объема продаж компьютеров в супермаркете за 10 рабочих дней (см. табл. 1).
Данные наблюдений представляют собой выборку, состоящую из n = 10 наблюдений. Простейшим способом организации данных в выборке является их группировка по возрастанию - данные при этом упорядочиваются по величине, т.е. записываются в виде последовательности x(1), x(2), … x(n), в которой x(1) ≤ x(2) ≤…≤ x(n). Последовательность упорядоченных по величине данных приведена во второй строчке таблицы. Разность между максимальным и минимальным элементами выборки x(n) - x(1), =R называется размахом выборки.
Исходные данные и статистические показатели
| Исходные данные, x(1), x(2), … x(n) | 1, 5, 5, 6, 2, 5, 6, 2, 6, 5 | n = 10 | ||||
| Упорядоченные, x(1 ≤ x(2 ≤…≤ x(n). | 1, 2, 2, 5, 5, 5, 5, 6, 6, 6 ,5,5,5,6 ,6,6 | R=5 | ||||
| Элементы выборки z(1)≠ z(2) ≠…≠ z(n) | zk | |||||
| - абсолютные частоты | nk | 10 ≡ n | ||||
| - относительные частоты | wk | 0,1 | 0,2 | 0,4 | 0,3 | |
| - накопленные частоты | Sk, | 0,1 | 0,3 | 0,7 | - | |
| - функция распределения | Fk(z) | 0,1 | 0,3 | 0,7 | - |
Следующим этапом организации выборки является подсчет частот, с которыми встречаются различные элементы выборки z(1), z(2),… z(n), где k ≤ n. - число различных чисел, содержащихся в выборке. Данная выборка содержит 4 различных числа: z(1), = 1, z(2), = 2, z(3), = 6.
Пусть число zj встречается в выборке nj раз, тогда это число (nj) называется частотой или абсолютной частотой элемента выборки zj. Эти частоты приведены в четвертой строчке таблицы. Очевидно, что сумма абсолютных частот равна числу наблюдений:
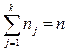 .
.
От абсолютных частот удобнее перейти к относительным, определяемым по отношению к объему выборки n:
 .
.
| со. = — ' п |
Очевидно, что сумма относительных частот равна единице, т.е.
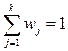
Последовательность пар (zj, wj) называют статистическим распределением выборки. Обычно статистическое распределение записывается в виде таблицы, первая строка которой содержит различные элементы выборки zj,, а вторая - их относительные частоты wj.
При неограниченном росте числа наблюдений относительные частоты значений zj, стремятся к вероятностям Рj = Рrob{Х=zj}, а статистическое распределение выборки переходит в закон распределения дискретной случайной величины X.
Получение статистического распределения объема продаж важно для определения наиболее вероятных объемов продаж и, следовательно, соответствующих запасов товара.
Наряду с частотами подсчитываются также накопленные частоты:
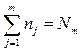
которые показывают, сколько раз в выборке встречаются значения, меньшие или равные данной величине, и накопленные (кумулятивные) относительные частоты:
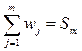
приведенные в пятой строчке таблицы.
Вместо кумулятивных частот часто подсчитывают выборочную функцию распределения Fn(х), определяемую по значениям накопленных частот:


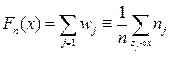
где суммируются частоты только тех элементов выборки, для которых выполняется неравенство zj, < х. Значения выборочной функции распределения приведены в последней строчке таблицы. Ее отличие от кумулятивной частоты состоит в том, что она показывает, какое относительное число раз в выборке встречаются значения, меньшие данной величины (а не меньшие или равные). Выборочная функция распределения представляет собой кусочно-постоянную неубывающую функцию, обращающуюся в нуль при x ≤ x(1) и принимающую значение "единица" при x >x(n).
Если рассматривать zk=k (дневное число продаж) в качестве значений случайной переменной Z, то при достаточно большом числе наблюдений относительные частоты появления значений zk будут стремиться к вероятности:
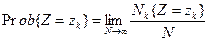 ,
,
а относительные накопленные частоты - к вероятности

которая является функцией конкретного значения z; и называется функцией распределения дискретной случайной величины Z.
1.10.4. Сравнение относительных частот в выборке и в генеральной совокупности. Репрезентативность выборки
Чрезвычайно важно при статистических исследованиях понимать сущность соотношения генеральной совокупности и случайной выборки, поскольку от этого часто зависит качество выводов с одной стороны и затраты на получение статистической информации с другой. Представление об этом соотношении может дать относительных частот в выборке и в генеральной совокупности. Относительной частотой появления события v(Аk) называется отношение числа опытов Nk, в которых произошло событие Аk, к полному числу испытаний N:
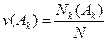
Например, подбрасывая монету N раз и подсчитывая число определенных исходов этого эксперимента, скажем, число выпадений орла Nорла , можно определить частоту появления данного исхода («орла» ) в серии испытаний как отношения числа испытаний, в которых выпал "орел", к общему числу испытаний (Nорла/N).
Проводя достаточно большое число опытов, можно заметить, что вначале, при малом числе опытов, частота появления какого либо события, казалось бы, ведет себя случайным образом, но с увеличением числа испытаний ее значение стабилизируется, стремясь к определенному пределу, который и называется вероятностью этого события. Формально, такое, вообще говоря, нестрогое определение вероятности Р(Аk) события Аk записывается так:
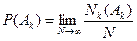 ,
,
если указанный предел существует.
Такое определение вероятности имеет смысл только при устойчивости частоты. Так, английский статистик Пирсон, подбросив монету 12000 раз, нашел, что частота появления "решки" составила при этом приблизительно 0,5069, а для 24000 бросаний - 0,5005, что приближается к классическому результату 0,5.
Еще одним простым примером является бросание игрального кубика. В этом случае вероятности (Р) выпадения любого числа очков (X) от 1 до 6 одинаковы и равны 1/6. Пусть генеральной совокупности соответствует распределение в верхней таблице, а некоторая выборка из нее представлена эмпирическим распределениями - в нижней:
Генеральная совокупность распределение случайной величины
| Х | ||||||
| Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Эмпирическое распределение случайной величины
| xk | ||||||
| wk | 0.16 | 0.17 | 0.17 | 0.16 | 0.17 | 0.17 |
Из таблиц видно, что относительные частоты в выборке близки к относительным частотам-вероятностям генеральной совокупности. Требование близости соответствующих частот соответствует понятию репрезентативности выборки.