Кривая имеет форму колокола.
2. Так как функция нормального распределения – чётная, то есть f(-t)=f(t), то кривая нормального распределения симметрична относительно максимальной ординаты, равной 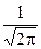 (при t=0). Абсцисса этой точки является центром распределения:
(при t=0). Абсцисса этой точки является центром распределения: 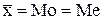 .
.
3. Ветви кривой, приближаясь к оси абсцисс, уходят в
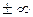 , т.к. функция нормального распределения принимает бесконечно малые значения при t=
, т.к. функция нормального распределения принимает бесконечно малые значения при t=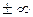 .
.
4. Кривая имеет две точки перегиба при  , находящиеся на расстоянии
, находящиеся на расстоянии 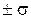 от
от 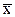 (среднего квадратического отклонения)
(среднего квадратического отклонения)
5. При 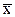 =const с увеличением s кривая становится более пологой.
=const с увеличением s кривая становится более пологой.
При s =const с изменением 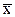 кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс.
кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс.
6. В промежутке  находится 68,3% всех значений признака.
находится 68,3% всех значений признака.
В промежутке 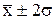 находится 95,4% всех значений признака.
находится 95,4% всех значений признака.
В промежутке  находится 99,7% всех значений признака
находится 99,7% всех значений признака
(правило трёх s).
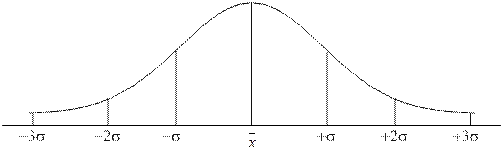
Рис. 5.3.1. Кривая нормального распределения
При сопоставлении эмпирической кривой с кривой нормального распределения необходимо проверить эмпирическую кривую на:
- симметричность;
- наличие одной нормальной вершины (не острой и не плоской).

Эмпирические кривые распределения бывают симметричные и асимметричные.
Для симметричных распределений частоты двух вариантов, равностоящих в обе стороны от центра, равны между собой.
Рассчитанные для симметричных рядов характеристики:
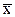 =Мо =Ме;
=Мо =Ме;  ;
;  ;
; 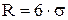
Если эти характеристики нарушены, то это свидетельствует о наличии асимметрии распределения.
Асимметричные кривые имеют правостороннюю или левостороннюю асимметрию – в зависимости от того, какая ветвь кривой вытянута (в первом случае – правая, во втором – левая).
Для того, чтобы измерить асимметрию, рассчитывают показатели асимметрии.
Наиболее известный среди них – структурный коэффициент асимметрии Пирсона:
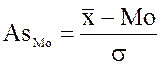 (5.3.3.)
(5.3.3.)
Если 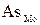 >0, то асимметрия правосторонняя. В этом случае Mo<Me<
>0, то асимметрия правосторонняя. В этом случае Mo<Me<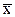 .
.
Если 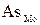 <0, то асимметрия левосторонняя. В этом случае Mo>Me>
<0, то асимметрия левосторонняя. В этом случае Mo>Me>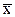 .
.
В симметричных рядах 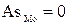 , асимметрия отсутствует
, асимметрия отсутствует
Для сквозной задачи:
 ,
,