Приведение матричной игры к задаче линейного программирования

Решение игры 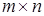может быть сведено к решению задачи линейного программирования.

Пусть игра 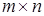задана платежной матрицей 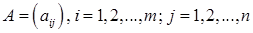. Первый игрок обладает 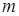, второй − 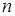стратегиями. Необходимо определить оптимальные стратегии первого 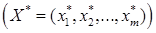и второго игрока, где − оптимальные частоты применения своих стратегий соответственно первым и вторым игроком.

.

Оптимальная стратегия X* обеспечивает первому игроку средний выигрыш, не меньший, чем цена игры V, при любой стратегии второго игрока и выигрыш, равный цене игры V, при оптимальной стратегии второго игрока.

Если первый игрок применяет смешанную стратегию X^* против любой чистой стратегии второго игрока, то он получает средний выигрыш, или математическое ожидание выигрыша V(j)=a_1jx₁+…a_mjx_m, j= 1, 2,…, п (т. е. элементы j-гo столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий первого игрока и результаты складываются).

Для оптимальной стратегии X^* все средние выигрыши не меньше цены игры V, поэтому получаем систему неравенств:

a₁₁x₁+a₂₁x₂+…+a_m1x_mV,

a₁₂x₁+a₂₂x₂+…+a_m2x_mV,

…………………….. (1.4.1)

a_1n x₁+a_2n x₂+…+a_mn x_mV.

 

Каждое из неравенств можно разделить на число V > 0. Введем новые переменные

z_i=. (1.4.2)

Тогда система (1.4.1) примет вид:

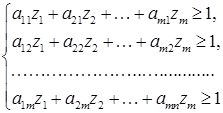(1.4.3)

Цель первого игрока — максимизировать свой гарантированный выигрыш, т. е. цену игры V. Разделив на равенство , получаем, что переменные удовлетворяют условию: .

Максимизация цены игры V эквивалентна минимизации величины 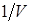, поэтому задача может быть сформулирована следующим образом: определить значения переменных так, чтобы они удовлетворяли линейным ограничениям (1.4.3) и при этом линейная функция

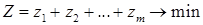(1.4.4)

обращалась в минимум. Это задача линейного программирования. Решая задачу (1.4.3) − (1.4.4), получаем оптимальные стратегии .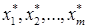

Для определения оптимальной стратегии 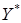второго игрока следует учесть, что он стремится минимизировать гарантированный выигрыш первого игрока, т. е. найти . Переменные удовлетворяют неравенствам

(1.4.5)

которые следуют из того, что средний проигрыш второго игрока не превосходит цены игры, какую бы чистую стратегию не применял первый игрок.

Если обозначить

(1.4.6)

то получим систему неравенств:

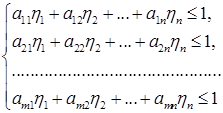(1.4.7)

Переменные , удовлетворяют условию .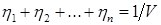

Игра свелась к следующей задаче: определить значения переменных 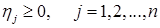, которые удовлетворяют системе неравенств (1.4.7) и максимизируют линейную функцию

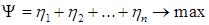(1.4.8)

Решение задачи линейного программирования (1.4.7) − (1.4.8) определяет оптимальную стратегию 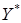. При этом цена игры

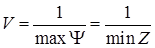. (1.4.9)

Задачи линейного программирования (1.4.3) − (1.4.4) и (1.4.7) − (1.4.8) являются взаимно двойственными. Очевидно, при определении оптимальных стратегий в конкретных задачах следует выбрать ту из взаимно двойственных задач, решение которой менее трудоемко, а решение другой задачи найти с помощью теорем двойственности.

 

2. Пример выполнения задания

 

Игра задана платежной матрицей А.

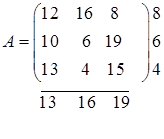
Для определения нижней цены игры 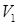выберем в каждой строке платежной матрицы минимальный элемент, затем из полученного столбца выберем максимальный элемент. Получим нижнюю цену игры: .

Для определения верхней цены игры 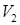выберем в каждом столбце матрицы максимальный элемент, тогда минимальный элемент из полученной строки и есть верхняя цена игры: .

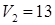Из условия следует, что игру необходимо проводить в смешанных стратегиях.

1) Пусть заданы вероятности использования противником своих стратегий: у = (0,2; 0,5; 0,3).

Необходимо определить оптимальное поведение и максимальный выигрыш первого игрока. Для этого рассчитаем его выигрыш в случае применения им всех своих стратегий по формуле:

При заданных условиях первый игрок должен применить свою третью стратегию, в этом случае он получит максимальный выигрыш равный 15,1.

2) Необходимо решить задачу 2x2, вычеркнув из заданной платежной матрицы столбец и строку таким образом, чтобы полученные в новой матрице 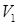и 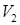не совпадали. Например, вычеркнем из исходной матрицы третью строку и первый столбец, получим новую матрицу:

у которой .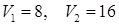

Решение задачи свелось к решению системы:

Используем формулу (1.3.2):

.

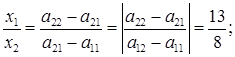
Вычислим выигрыш первого игрока:

;

.

Отсюда вывод: первому игроку следует использовать свои стратегии с частотой , при этом его гарантированный выигрыш будет равен 12,19 ед., что существенно выше чем .

Для второго игрока решение сведется к системе:

; .

.

Используя смешанные стратегии с частотой , второй игрок может понизить свой гарантированный протгрыш с 16 ед. до 12,19 ед.

3) Игра .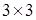

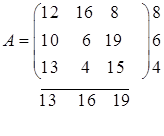
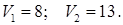
Любая игра сводится к задаче линейного программирования. Для первого игрока ограничения и целевая функция выглядят следующим образом:

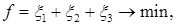
где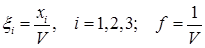

Для решения полученной задачи используем симплекс-метод, реализованный в программе LINPROG. При этом получим оптимальное решение:

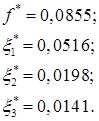
Перейдем к исходным переменным:

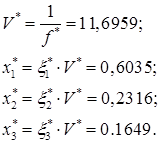
Из полученных результатов следует, что максимальный гарантированный выигрыш первого игрока составит 11,6959 при условии, что он будет применять свою первую стратегию с частотой 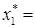0,6035, вторую − с частотой 0,2316 и третью − с частотой 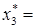0,1649.

Для второго игрока задача линейного программирования является двойственной к предыдущей и имеет вид:

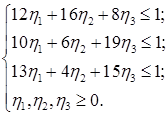
где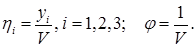

Для решения использовалась программа LINPROG. Полученное оптимальное решение имеет вид:

Перейдем к исходным переменным:

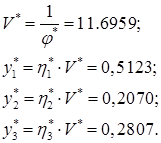
Из полученных результатов следует, что минимальный гарантированный проигрыш второго игрока составит 11,6959 в случае если он будет использовать свою первую стратегию с частотой 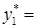0,5123, вторую − с частотой 0,2070, третью − с частотой 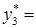0,0240.