По сгруппированным данным
(n велико)
| xi | x1 | x2 | … | xi | … | xl |
| mi | m1 | m2 | … | mi | … | ml |
mi – частота встречаемости значения признака xi; 
- объём выборки
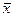
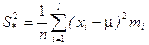
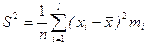или
или
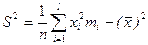
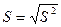
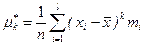
, n=2·l-1
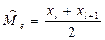, n=2· l
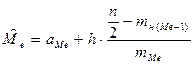
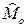=xi с наибольшей частотой встречаемости
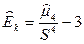
2 взгляда на выборку: 1) Под выборкой объёма n из генеральной совокупности понимается n наблюденных результатов испытания, например, n измерений (числовых и нечисловых) некоторого признака или нескольких признаков. 2) Под выборкой понимается система n независимых случайных величин, распределенных одинаково и так же, как генеральная совокупность или случайная величина Х.
Получив статистические оценки параметров распределения (выборочное среднее, выбороч-ную дисперсию и т.д.), нужно убедиться, что они в достаточной степени служат приближением соответствующих характеристик генеральной совокупности
Статистическая оценка Θ* называется несмещенной, если ее математичес-кое ожидание равно оцениваемому параметруΘ при любом объеме выборки:
М(Θ*) = Θ.
Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.
Статистическая оценка называется эффективной, если она при заданном объеме выборки п имеет наименьшую возможную дисперсию.
Состоятельной называется статистическая оценка, которая при п→∞ стре-мится по вероятности к оцениваемому параметру (если эта оценка несмещенная, то она будет состоятельной, если при п→∞ ее дисперсия стремится к 0).
2 Выборочные моменты. Вывести формулы, устанавливающие связь между центральными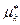 
и начальными 
выборочными моментами для 
.
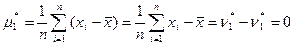
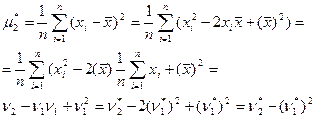
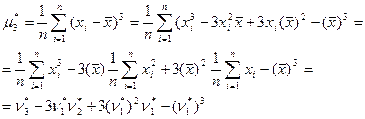
3 Медиана – значение признака ряда, относительно которого ряд делится на 2 равные по числу признаков части. Таким образом, медиана Ме равна:
1.при нечетном числе наблюдений n=2l-1 - значению признака Х, приходящегося на середину ранжированного ряда наблюдений:
2.при четном числе наблюдений n=2l –средней арифметической двух значений, расположенных в середине ранжированного ряда:
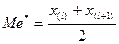
Если исходят из интервального ряда, то медиана вычисляется по формуле:
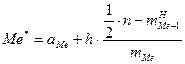
Гдеh – длина интервала, n – объем выборки
Мода – значение признака, которому соответствуют наибольшая частота. Для одномодального интервального ряда вычисление моды производится по формуле
Если Xср, Мо и Ме почти не отличаются друг от друга, то есть основания предполагать теоретическое распределение изучаемого признака симметричным. При изучении экономических явлений симметричные ряды встречаются довольно редко. Когда распределение набора данных скошено в правую сторону больше, чем в левую, то говорят о правосторонней асимметрии. При скосе в левую – о левосторонней. При правосторонней асимметрии средняя находится справа от медианы, которая лежит справа от моды. Для левосторонней – наоборот. Чем более асимметрично распределение признака, тем больше расхождения между значениями средней арифметической, медианы и моды.
Коэффициент асимметрии Ас – показатель асимметричности распределения, определяющий степень скошенности кривой по сравнению с нормальным распределением, и вычисляемый по формуле:
Для симметричных В.Р. Ас=0, для правосторонней асимметрии – Ас >0, левосторонней – Ас<0. Если |Ас|>0,5, то асимметрия существенна.
Коэффициент эксцесса Ек – показатель, служащий мерой крутости (плосковершинности или островершинности) графику В.Р. в сравнении с кривой нормального распределения, определяемый по формуле:
Если Ек>0, то график островершинный, Ек<0 – плосковершинный.
Коэффициент вариации Vs – безразмерный показатель меры рассеяния значений изучаемого признака и равный процентному отношению среднего квадратического отклонения к средней арифметической: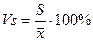
Если к.в. признака высок (более 100%), это свидетельствует о неоднородности значений признака.
Соотношения МОМЕНТОВ : 
4.Точечные оценки и их свойства. Проверить оценки математического ожидания и дисперсии нормальной генеральной совокупности (
, S2 и Ŝ2), полученные по выборке 
, на несмещенность и состоятельность.
Точечной оценкой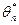 
параметра θ называют функцию от результатов наблюдений 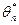(х1, х2,… хn), значение которой принимают за наилучшее приближение к оцениваемому параметру θ. К точечным оценкам предъявляют требования несмещенности, эффективности, состоятельности и достаточности.
1. Статистическая оценка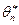
параметра 
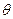н-ся несмещенной, если при любой объеме выборки n её математическое ожидание равно оцениваемому параметру: 
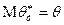.Если оценка является смещенной, то смещение определяется как 
. Требование несмещенности является минимальным требованием, т.к. зная величину смещения, оценку можно всегда скорректировать.
2 Статистическая оценка 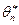параметра 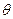н-ся эффективной, если при заданном объеме выборки она имеет наименьшую возможную дисперсию среди всех возможных несмещенных оценок. При этом, согласно неравенству Рао-Камера, дисперсия любой несмещенной оценки параметра 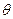ограничена снизу:
,где 
- плотность распределения вероятностей случайной величины.
3 Статистическая оценка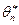параметра 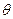называется состоятельной, если она удовлетворяет закону больших чисел, т.е. при 
сходится по вероятности к оцениваемому параметру:
или 
. -состоятельная оценка μ только при независимых наблюдениях. В противном случае - несостоятельна.
4 Статистическая оценка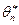параметра 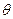называется достаточной, если содержит всю информацию об оцениваемом параметре, то есть такую оценку 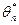параметра θ, когда условное распределение f(|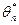=d) не зависит от d – конкретного значения .
· 
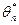так как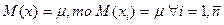 
несмещенная оценка 
· 
Bn=0 => оценка несмещенная
оценка состоятельности:
1)Bn=0
2)
· 
· 
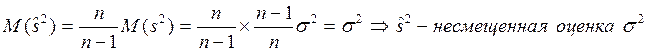
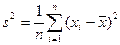
Везде Q нужнозаменить на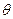
5 эффективность и асимптотическая эффективность точечной оценки. неравенство рао-крамера. Доказать, что средняя арифметическая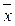 
, полученная по результатам выборки из генеральной совокупности, имеющей экспоненциальный закон распределения с плотностью … является эффективной оценкой параметра λ.
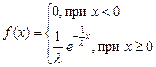
Точечная оценка – некоторая ф-ия результатов наблюдений 
(х1…хn), значение которой принимают за наилучшее приближение в данных условиях к значению параметра Q ген. Совокупности Х.
Эффективной называется точечная оценка, обладающая наименьшей дисперсией среди всех возможных несмещенных оценок параметра Q при данном объеме выборки. Эффективность оценки хар-ся средним квадратом отклонений
(-
.
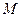Неравенство Рао-Крамера ограничивает дисперсию любой несмещенной оценки параметра Q снизу:
.
Количество информации Фишера о параметре Q,
Содержащейся в единичном наблюдении
=
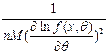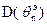. Эффективность параметра определяется соотношением 
. 
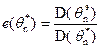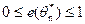
Если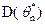 
совпадает с нижней границей, то оценка эффективна.
Однако существование эффективной оценки это довольно сильное требование на задачу. Более слабым является условие асимптотической эффективности, которое означает, что отношение дисперсии несмещенной оценки к нижней границе Крамера-Рао стремится к единице при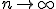 
,т.е.
Решение
1. 
= 
= 
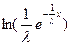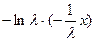
2. 
= 
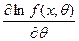3. I = M ()
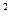=M (
)
=
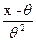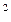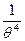M(x-)=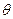
=
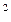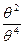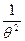
4. 
=
.
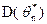
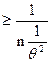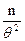т.к. 
,то оценка эффективна. Эффективная оценка является и достаточной
6 Достаточность точечной оценки. Критерий факторизации. Доказать достаточность средней арифметической 
, используемой в качестве оценки параметра λ пуассоновского закона распределения 
.
Достаточной называется оценка 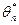,если условное распределение , где d конкретное зн-е 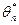не зависит от параметра 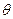для любого 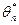.Достаточность оценки проверяется с помощью критерия факторизации, когда функция правдоподобия L(Х1,…,Хn/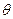) может быть представлена в виде произведений двух сомножителей: 1-й зависит от 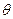и 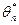,а 2-й от х. То есть L(Х1,…,Хn/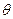) = G (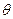;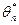) * Н(Х1,…,Хn). Эффективная оценка является и достаточной.
МНЕ КАЖЕТЯ,ЧТО ТУТ ОПЕЧАТКА, И ДОЛЖНО БЫТЬ
В УСЛОВИИ
ЕСЛИ ТАМ ОПЕЧАТКА,ТО:
Решение. L(Х1,…,Хn/
) = 
=
=
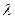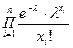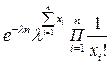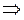оценка достаточна
G (;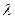
) Н(Х1,…,Хn).
ЕСЛИ нет ОПЕЧАТКИ,ТО:
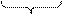Решение. L(Х1,…,Хn/) = 
=
=
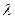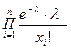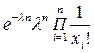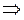оценка достаточна
G Н(Х1,…,Хn).
7. Методы получения точечных оценок. Свойства оценок метода моментов и метода максимального правдоподобия. Найти оценку наибольшего правдоподобия параметра p биномиального закона распределения по результатам k независимых выборок объемов 
, в которых некое событие произошло соответственно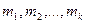 
раз.
Метод моментов
Метод моментов предложил Карл Пирсон. Согласно этому методу по выборке определяется столько начальных моментов, сколько параметров необходимо оценить.
Например: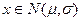 
-> 2 параметра -> для определения оценки параметров ищем 
и 
, а остальные параметры -> функции от и .
= 
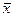
Оценки метода момента состоятельны, однако, их эффективность часто бывает значительно < 1.
Метод максимального правдоподобия
В 1925 Р. Фишер критикует метод моментов и предлагает метод максимального правдоподобия, основу которого составляет функция правдоподобия.
Пусть - выборка из генеральной совокупности Х с функцией плотности f(x; θ), где θ – вектор неизвестных параметров, которые подлежат оценке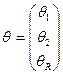 
Функция правдоподобия – вероятность или плотность вероятностей совместного наступления событий при заданном значении θ. Т. е L(|θ)=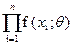
, т.к. взаимно независимые, в качестве вектор оценок θ принимается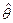 
, который максимизирует L или ln L.
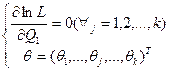Если у 
существует эффективная оценка, то она совпадает с оценкой максимального правдоподобия.
Свойства: 1) Если у θ существует эффективная оценка 
, то эта оценка совпадает с оценкой максимального правдоподобия. 2) Асимпт. свойство – оценки максимального правдоподобия – состоятельные, асимптотически эффективные и имеют асимптотически нормальный закон распределения.
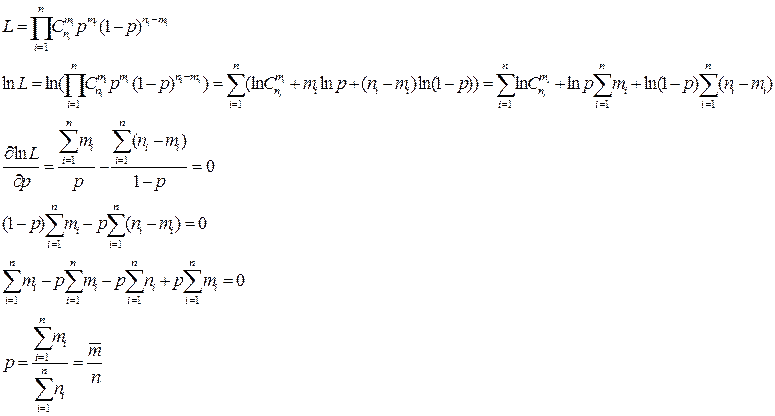
8. Точные и асимптотические законы распределения выборочных характеристик. Вывести закон распределения в предположении, что выборка взята из нормальной генеральной совокупности Х.
Законы распределения выборочных характеристик.
Знание законов необходимо для построения интервальных оценок. Рассматривают точные и асимптотические законы выборочных характеристик.
Асимптотические интервальные законы распределения Qn*, к которым стремится точное распределение при n → ∞.
Точные з-ны распределения.