Критерий Кохрана
Пусть Х1, Х2 ,…, Хl – l нормал. генер. сов., из котор. извлечены незав. случ. выборки одинак. объема 
; 
– исправ. выбор. дисперсии.
На уровне знач.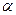 
провер. нулев. гип. о рав-ве дисп. l генер. сов., т.е. 
.
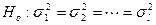Выбороч. х-ка критерия:
, котор. при выпол. нулев. гип. имеет G-распределение с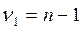 
и 
, где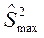 
– наибольш. из исправ. выбор. диспер.
Для проверки нулев. гип. строят правостор. крит. обл., границу котор. опред. по табл. G-распределения из условия:
.
Критерий проверки: если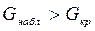 
, то гипотезу отвергают, если же 
, то считают, что гипотеза не противоречит опытным данным.
25 Проверка гипотезы однородности ряда вероятностей в случае биноминального распределения.
Пусть Х1, Х2 ,…, Хl – l генер. сов., каждая из котор. характериз. неизв. параметром Pi, где Pi – вероят. появл. события А в соотв. выборке.
Требуется провер. нулев. гип. о рав-ве вероят. появлен. события А в генер. совокупностях, т.е. 
.
Для проверки гип. использ. статистику:
, где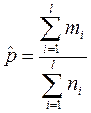 
– средн. частость появлен. события А по всем выборкам.
Или, используя частости по всем выборкам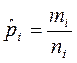 
:
.
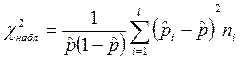Статистика 
при выполн. нулев. гип. имеет асимптотическое распред.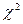 
с l-1 степ. свободы, где l – число генер. совокуп.
Для проверки нулев. гип. на уров. знач. 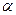строят правостор. крит. обл., границу 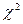котор. опред. из условия:
.
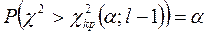Критерий проверки: если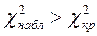 
, то гипотезу отвергают, если же 
, то считают, что гипотеза не противоречит опытным данным.
26 Проверка гипотезы однородности ряда вероятностей в случае полиномиального распределения.
Пусть X1, X2…Xl – l генеральных совокупностей, из которых взяты случайные независимые выборки объемом n1=n2=…=nl и пусть ni элементов i-й выборки классифицируются по какому-либо признаку на h групп с числом элементов в каждой группе mi1, mi2,…mij, mih, где j=1,2…h
для всех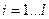 
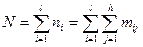- общее число набл по всем выборкам
Н0: 
для всех j=1,2,…h т.е. вероятность попадания элемента в соответствующую группу равна для всех совокупностей
Н1 :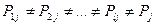 
В основу критерия положена статистика: 
Где 
для всех j=1,2…h
При справедливости нулевой гипотезы Н0 статистика 
имеет распределение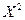 
с 
степенями свободы. Для проверки нул. гипотезы на уровне значимости 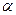строят правостороннюю критическую область, границы к-рой опред-ся из условия:
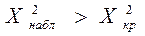=> отвергается с вероятностью ошибки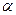
=> гипотеза не противоречит опытным данным