Лабораторная работа № 14

 

РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ ГРАДИЕНТНЫМИ МЕТОДАМИ

 

1. Цель работы.

 

Научиться использовать ЭВМ для определения экстремума функции двух переменных методом градиентного спуска (подъема).

 

2. Исходные данные

 

2.1. Функция двух переменных, вид экстремума и начальные значения аргументов выбираются из табл. 1 в зависимости от номера варианта.

2.2. Начальное значение параметра, определяющего длину шага поиска: h = ⁺ 0.05.

2.3. Максимальное число итераций m=200.

2.4. Минимальное значение модуля градиента Ед = 0,005;

минимальное приращение аргумента Ех = 0,001.

Таблица 1

Варианты исходных данных

 

Ва- ри- ант	Функция f (x1,x2)	Вид экстре- мума	Координаты начальной точки
x1(0)	x2(0)	x1(0)	x2(0)
	2*(x1-2)2+(x2-3)4+1	min
	(x1-1)4+3*(x2-2)2+2	min
	2*(x1+3)2+0.5*(x2-4)4+3	min	-2		-4
	(x1+2)4+2*(x2-1)2+4	min	-1		-3
	-(x1-2)2-0.5*(x2-1)4-5	max
	-2*(x1+3)2-(x2-2)4-6	max	-2		-4
	-(x1-1)4-3*(x2-3)2-7	max
	-2*(x1-5)2-(x2-4)4+8	max
	-0.5(x1+4)4-(x2-1)2+9	max	-5		-3
	-(x1-2.5)2-(x2+3)4+10	max		-2		-4
	-(x1+3.5)4-3*(x2+4)2+11	max	-5	-5	-2	-3
	(x1+5)4+2*(x2+2)2-12	min	-4	-1	-6	-3
	(x1-1.5)2+(x2+2.5)4-13	min		-4		-1
	0.5*(x1-4.5)4+(x2-5.5)2-14	min

 

3. Содержание работы

 

3.1. Разработать алгоритм и программу для определения экстремума функции двух переменных градиентным методом.

 

3.2. По разработанной программе на ЭВМ провести поиск экстремального значения функции. В процессе поиска через каждые 10 итераций на печать выводить номер итерации, модуль градиента и значения аргументов.

По окончании поиска напечатать оценки оптимальных значений аргументов и экстремального значения функции, значение параметра h и число итераций.

3.3. Изменяя параметр h в интервале h= ⁺ 0.05... ⁺ 0.2 с шагом ⁺ 0.05, исследовать влияние параметра на скорость поиска.

3.4. Построить график зависимости числа итераций, необходимых для нахождения экстремума, от величины параметра h.

 

4. Теоретические основы работы

 

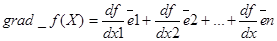Градиент ─ это вектор, который показывает направление наискорейшего возрастания функции. Для функции n переменных W = f (X) градиент записывается в виде

 

 

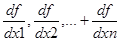
где - частные производные функции, которые являются проекциями

 

градиента на координатные оси;

где ─ единичные векторы (орты).

 

Модуль градиента равен наибольшей скорости возрастания функции в данной точке

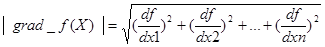Вектор, направленный противоположно градиенту и равный ему по величине, называется антиградиентом.

Для проведения поиска градиентным методом вначале выбирается произвольная точка М0, принадлежащая области определения оптимизируемой функции. Затем :

1) определяется направление градиента в точке М0;

2) осуществляется перемещение из точки М0 на величину, равную некоторому шагу, в точку М1, причем перемещение проводится в направлении градиента, если ищется максимум функции и в направлении антиградиента, если ищется минимум функции ;

3) в точке М1 устанавливается новое градиентное направление и делается следующий шаг в новую точку и т.д.

Значение каждой координаты хj в конце к-го шага определится по формуле

где h ─ параметр, определяющий длину шага ;

cкорость изменения функции по координате xj в точке Х^(k)

 

Таким образом, градиентный метод обеспечивает на каждом шаге изменение всех независимых переменных, причем каждая переменная получает приращение, пропорциональное соответствующей составляющей градиента по данной оси.

При поиске минимума движение происходит в антиградиентном направлении, поэтому параметр h берется со знаком "минус".

Рекомендуется придерживаться следующей схемы поиска :

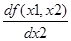1) определить значения проекций градиента в точке (х1,х2)

 

2) вычислить модуль градиента

если , то перейти к п.6;

 

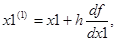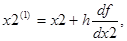3) определить координаты очередной точки

4) проверить условия окончания поиска

 

│х1 ⁽¹⁾ ─ х1│ <= Ех , │х2 ⁽¹⁾ ─ х2│ <= Ех ,

 

в случае их выполнения перейти к п.6 ;

5) перейти в новую точку

 

х1 = х1⁽¹⁾ , х2 = х2⁽¹⁾

 

и возвратиться к п.1;

6) вычислить оценку экстремального значения функции

f (x1 ⁽¹⁾ , x2 ⁽¹⁾ )

 

 

5. Содержание отчета

 

5.1. Цель работы.

5.2. Исходные данные.

5.3. Расчетные формулы с пояснениями.

5.4. Схема алгоритма поиска.

5.5. Распечатка программы и результатов оптимизации.

5.6. График зависимости необходимого числа итераций от величины

параметра h.

5.7. Выводы.