рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Спорт
- /
- Лабораторная работа № 2
Реферат Курсовая Конспект
Лабораторная работа № 2
Лабораторная работа № 2 - раздел Спорт, По дисциплине Математические модели в транспортных системах. Организация дорожного движения Принятие Решений В Условиях Неопределенности 1. Цель...
ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
1. Цель работы
Изучить принципы принятия решений при неопределенном состоянии внешней среды.
2. Исходные данные
2.1. Параметры А, В и С для расчета полезности результатов принимаются по табл. 1 в зависимости от номера варианта.
Таблица 1
Варианты значений исходных параметров
| N варианта | ||||||||||||||
| A | ||||||||||||||
| B | ||||||||||||||
| C |
2.2. Количество стратегий М и количество возможных состояний среды N принимается по одному из двух вариантов:
1) М=4, N=6;
2) М=6, N=4;
3. Содержание работы
3.1. В соответствии с указаниями, приведенными в п.2.4.1 составить алгоритм заполнения матрицы полезности результатов и вывода матрицы на печать в виде таблицы.
3.2. Разработать алгоритм и программу для определения оптимальной стратегии в условиях неопределенности по критерию Лапласа.
3.3. В соответствии с заданной матрицей полезности результатов рассчитать оптимальную стратегию.
4. Теоретические основы работы
4.1. Полезность результата U(I,K), которая достигается путем использования стратегии Х(I) при состоянии среды S(K), рассчитывается следующим образом:
U(l,l) = -10*А;
U(2,l) = -11*В;
U(3,l) = -12*С;
U(4,l) = -13*(А+В);
U(5,1) = -14*(B+C);
U(6,1) = -15*(A+B);
Для остальных элементов матрицы ;
U(I,K) = U(I,K-1) + ABS(U(I,1)) + K – I,
K=2…N; I=1…M
Получаемые значения U(I,K) следует заносить в матрицу полезности результатов, которая составляется по форме, приведенной в табл. 2
Таблица 2
Матрица полезности результатов
| S(K) X(I) | S(l) | S(2) | … | S(N) |
| X(l) | U(l,l) | U(l,2) | … | U(1,N) |
| X(2) | U(2,l) | U(2,2) | … | U(2,N) |
| … | … | … | … | …. |
| X(M) | U(M,1) | U(M,2) | … | U(M,N) |
2.4.2.
 |
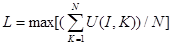Для определения оптимальной стратегии по критерию Лапласа используется следующее решающее правило:
 |  | ||
где L - полезность, соответствующая оптимальной стратегии.
В соответствии с приведенным решающим правилом для каждой стратегии необходимо определить среднюю полезность результата (предполагается, что появление любого состояния среды равновероятно), а затем из полученного ряда средних полезностей выбрать максимальное значение L. Та стратегия Х(I), которой соответствует максимальная средняя полезность L, и является оптимальной.
5. Содержание отчета
5.1. Цель работы
5.2. Исходные данные
5.3. Матрица полезности результатов
5.4. Схема алгоритма принятия решения по критерию Лапласа
5.5. Распечатка программы и результатов расчета
5.6. Выводы
– Конец работы –
Эта тема принадлежит разделу:
По дисциплине Математические модели в транспортных системах. Организация дорожного движения
Белорусский национальный технический университет Кафедра Организация автомобильных перевозок и дорожного движения...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Лабораторная работа № 2
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?
Подпишитесь на Нашу рассылку
Реклама
Информация в виде рефератов, конспектов, лекций, курсовых и дипломных работ имеют своего автора, которому принадлежат права. Поэтому, прежде чем использовать какую либо информацию с этого сайта, убедитесь, что этим Вы не нарушаете чье либо право.
© copyright 1999 - 2024 allRefs.net. Все права защищены. Страница сгенерирована за: 0.031 сек.
Новости и инфо для студентов