Лабораторная работа № 6

ИССЛЕДОВАНИЕ РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН

 

1. Цель работы

 

Изучить методику проверки согласия эмпирического и теорети­ческого распределений случайной величины.

 

2. Исходные данные

 

Выборка случайной величины (40 значений), полученная в ре­зультате выполнения лабораторной работы № 4.

Исходные данные записать в файл RNDID..DAT.

 

3. Содержание работы

 

3.1. По программе RND.EXE произвести расчеты по определе­нию статистических характеристик случайной величины и аппроксима­ции ее эмпирического распределения теоретическим законом наиболее подходящим по критерию Романовского. Результаты расчета содержатся в файле RNDNR.

3.2. Повторить аппроксимацию эмпирического распределения теоретическим законом, указанным в задании лабораторной работы № 4.

3.3. Проверить гипотезу о согласовании эмпирического и за­данного теоретического распределений по критерию хи - квадрат при уровне значимости alfa = 0,2 и 0,05 и по критерию Мизеса-Смирнова (омега-квадрат) при alfa = 0,2 и 0,1.

3.4. Построить графики эмпирической и теоретической функций распределения и проверить гипотезу о согласовании эмпирического и заданного теоретического распределений по критерию Колмогорова при уровне значимости alfa = 0,1.

 

4. Теоретические основы работы

 

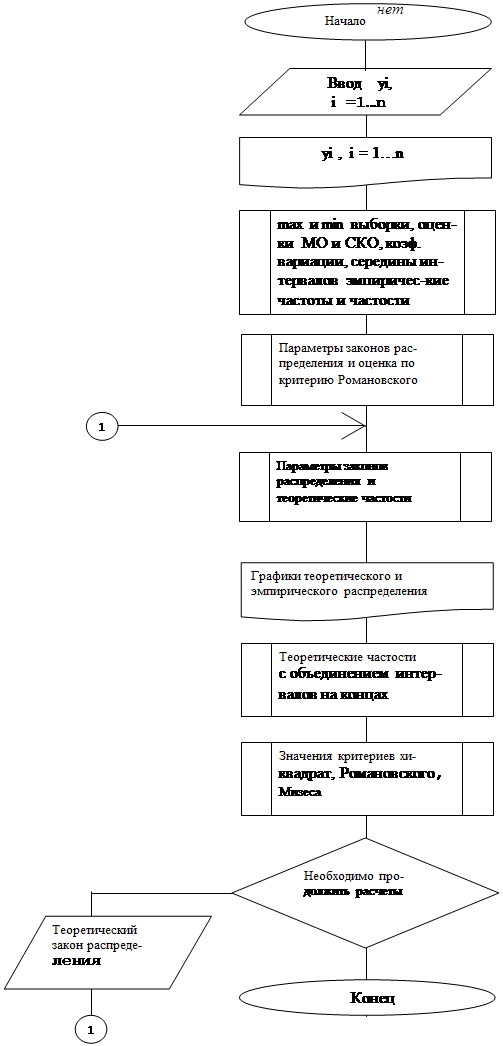
Структурная схема алгоритма программы RND для исследования распределений случайных величин приведена на рис. 1

После обращения к программе задают вид распределения случай­ной величины (в данном случае непрерывное) и в качестве наимено­вания данных вводят номер учебной группы, номер варианта и вид закона распределения (указанный текст набирается через пробелы без запятых). Затем задают объем выборки и поочередно вводят слу­чайные числа. По завершении ввода, при необходимости, в исходные данные вносятся исправления, для чего следует положительно отве­тить на соответствующий вопрос программы и набрать порядковый номер числа, которое необходимо исправить.

Число интервалов следует задавать равным значению, рекомен­дуемому программой, а величину смещения принимать равной 0.

Затем необходимо выбрать наилучшее теоретическое распределе­ние по критерию Романовского. Это достигается в результате поло­жительного ответа на соответствующий вопрос программы.

На следующем этапе рекомендуется получить графики теорети­ческого и эмпирического распределений, а также помимо значений критериев хи-квадрат и Романовского - значение критерия Мизеса.

В дальнейшем следует продолжить расчет (положительно ответить на соответствующий вопрос) и, не изменяя числа интервалов и величины смещения, ввести порядковый номер тре­буемого закона распределения из списка, предложенного программой. После получения значений параметров распределения, теоретических частостей и значений критериев расчет можно закончить.

Для проверки гипотезы о согласовании теоретического и эмпи­рического распределений по критерию хи-квадрат необходимо по таб­лице найти граничные значения хи-квадрат при заданных уровнях значимости и известном числе степеней свободы (взять из распечат­ки результатов расчета). Затем следует сравнить значение хи-квадрат, полученное в результате расчета, с табличными значениями и сделать соответствующие выводы о подтверждаемости гипотезы при различных уровнях значимости.

С целью проверки гипотезы по критерию Мизеса-Смирнова следу­ет по таблице найти значение функции распределения статистики омега-квадрат в точке, полученной в результате расчета (значение критерия Мизеса в распечатке). Найденное значение необходимо срав­нить с доверительными вероятностями, которые определяются по за­данным уровням значимости, и сделать соответствующие выводы о подтверждаемости гипотезы.

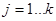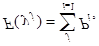Для построения графиков эмпирической и теоретической функций распределения используются эмпирические и теоретические частости, которые имеются в распечатке результататов расчета. Поскольку фун­кция распределения представляет собой накопленные частости, фор-мулы для расчета эмпирической F_э(y_j) и теоретической F(y_j) фун­кций распределения имеют вид:

где m_i/n - эмпирические частости; P_i - теоретические час­тости; y_j - правая граница j -гo интервала; k-число интервалов. Значения y_j определя-ются на основании значений середин интерва­лов, приведенных в распечатке.

Для каждого y_j вычисляется модуль разности между эмпирической и теоретической функциями распределения АВS(F_э(у_j) - F(y_j)).

Результаты расчетов следует свести в таблицу 1.

 

Таблица 1

Данные для проверки гипотезы по критерию Колмогорова

 

Интервалы значений случайной величины [y(j-i),yj[	Эмпири- ческие частос- ти mj/n	Теорети- ческие частости Pj	Эмпиричес- кая функ- ция Fэ(yj)	Теорети- ческая функция F(yj)	ABS(Fэ(yj)-F(yj))

 

Из последнего столбца таблицы выбирается наибольший модуль разности между эмпирической и теоретической функциями распреде­ления

 

D = max ABS(F_э(y_j)-F(y_j)) , j = l...k.

 

Вычисляется значение критерия Колмогорова

 

При заданном уровне значимости по таблице определяют гранич­ное значение LAMBDA(alfa), проверяют условие LAMBDA < LAMBDA(alfa) и делают соответствующий вывод о согласовании, теоретического и эмпирического распределений.

Необходимо помнить, что для проверки гипотезы используют те значения критериев и те теоретические частости, которые были полу­чены для заданного теоретического закона распределения.

 

5. Содержание отчета

 

5.1. Цель работы

5.2. Исходные данные

5.3. Структурная схема алгоритма программы RND

5.4. Результаты расчета на ЭВМ

5.5. Графики эмпирической и теоретической функций распределения

5.6. Проверка согласия эмпирического распределения с теоретическим по заданным критериям

5.7. Выводы