рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Спорт
- /
- ЛІНІЙНЕ ПРОГРАМУВАННЯ. Транспортна задача. ЦІЛОЧИСЛОВЕ ПРОГРАМУВАННЯ
Реферат Курсовая Конспект
ЛІНІЙНЕ ПРОГРАМУВАННЯ. Транспортна задача. ЦІЛОЧИСЛОВЕ ПРОГРАМУВАННЯ
ЛІНІЙНЕ ПРОГРАМУВАННЯ. Транспортна задача. ЦІЛОЧИСЛОВЕ ПРОГРАМУВАННЯ - раздел Спорт, Міністерство Освіти І Науки, Молоді Та Спорту України Криворізький Т...
Міністерство освіти і науки, молоді та спорту України
Криворізький технічний університет
Кафедра економіки, організації та управління підприємствами
МЕТОДИЧНІ ВКАЗІВКИ
Кривий РігЗМІСТ
1. Загальні положення ............................................................... 4
2. Основи оптимального управління ....................................... 5
3. Лінійне програмування ........................................................ 6
3.1. Загальна постановка задачі .................................. 6
3.2. Види математичних моделей .............................. 8
3.3. Графічний розв’язок систем т лінійних нерівностей
з двома змінними .................................................. 10
3.4. Графічний метод ................................................... 13
3.5. Симплексний метод ............................................. 15
3.6. Транспортна задача ............................................. 18
4. Цілочислове програмування ............................................... 24
4.1. Загальна постановка задачі .................................. 24
4.2. Метод Гоморі ....................................................... 25
4.3. Графічний метод .................................................. 27
5. Нелінійне програмування .................................................. 27
5.1. Загальна постановка задачі ................................... 27
5.2.Дробово-лінійне програмування .......................... 28
5.3. Метод множників Лагранжа ................................. 33
5.4. Дослідження функції на екстремум за заданою
областю припустимих розв’зків ............................ 34
6. Модель Лєонтьєва багатогалузевої економіки (балансовий
аналіз) ....................................................................................... 34
7. Динамічне програмування ..................................................... 36
7.1. Загальна постановка задачі ................................... 36
7.2. Оптимальна стратегія заміни обладнання .......... 38
7.3. Оптимальний розподіл ресурсів .......................... 41
7.4. Оптимізаційна модель управління товарними
запасами .................................................................. 42
8. Контрольні завдання .............................................................. 49
9. Зразки розв’язання задач .................................................... 69
10. Список використаних джерел .......................................... 95
ЗАГАЛЬНІ ПОЛОЖЕННЯ
1) математична формалізація задачі у вигляді побудови економіко-математичної моделі; 2) визначення типу задачі (лінійного, нелінійного, динамічного програмування… 3) визначення способу розв’язання оптимізаційної задачі;ОСНОВИ ОПТИМАЛЬНОГО УПРАВЛІННЯ
Задачі управління і планування зазвичай зводяться до вибору деякої системи параметрів і системи функцій. Нехай необхідно знайти максимум (мінімум)… (2.1)ЛІНІЙНЕ ПРОГРАМУВАННЯ
Загальна постановка задачі
Ця лінійна функція називається цільовою, а обмеження які математично записуються у вигляді рівнянь або нерівностей називаються системою обмежень. … Математичне вираження цільової функції та її обмежень називається математичною… У загальному вигляді математична модель задачі лінійного програмування можна записатиВиди математичних моделей
Якщо всі обмеження системи задано рівняннями і змінні є невід’ємними, тоді таку модель називають канонічною. Якщо хоча б одне обмеження є… Для переходу від неканонічної до канонічної моделі необхідно у кожну… Таким чином, щоб скласти математичну модель задачі лінійного програмування необхідно:Графічний розв’язок систем т лінійних нерівностей з двома змінними
(3.1)Графічний метод
З геометричної точки зору у задачах лінійного програмування відшукується така кутова точка або набір точок із припустимої множини розв’язків, на… Для знаходження екстремального значення цільової функції при графічному… З курсу вищої математики відомо, що для функції двох змінних , що є диференційованою у точці , градієнтом функції…Симплексний метод
Ідея симплекс-методу або методу послідовного покращення плану полягає у тому, що починаючи з деякого початкового опорного рішення здійснюється… Опорним розв’язком називають базисний невід’ємний розв’язок. Алгоритм симплексного методуТранспортна задача
Транспортна задача – одна з розповсюджених задач лінійного програмування. Її мета – розробка найбільш раціональних шляхів і способів транспортування товарів, усунення найбільш віддалених, зустрічних, повторних перевезень. Все це скорочує час просування товарів, зменшує витрати підприємств, пов’язаних із здійсненням процесів забезпечення сировиною, матеріалами, паливом, обладнанням тощо.
У загальному вигляді задачу можна представити наступним чином: у т пунктах виробництва  маємо однорідний вантаж відповідно у кількості
маємо однорідний вантаж відповідно у кількості 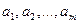 . Цей вантаж необхідно доставити у п пунктів призначення
. Цей вантаж необхідно доставити у п пунктів призначення 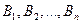 відповідно у кількості
відповідно у кількості 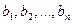 . Вартість перевезення одиниці вантажу (тариф) із пункту
. Вартість перевезення одиниці вантажу (тариф) із пункту 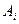 до пункту
до пункту 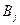 дорівнює
дорівнює 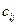 .
.
Необхідно скласти план перевезень, яких дозволяє перевезти весь вантаж при мінімальних транспортних витратах.
У залежності від співвідношення між сумарними запасами вантажу і сумарними потребами у них, транспортні задачі можуть бути закритими і відкритими.
Якщо 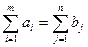 , тоді транспортна задача називається закритою.
, тоді транспортна задача називається закритою.
Якщо 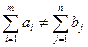 , тоді транспортна задача називається відкритою.
, тоді транспортна задача називається відкритою.
Позначимо через  кількість вантажу, який перевозять з пункту
кількість вантажу, який перевозять з пункту 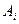 до пункту
до пункту 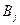 .
.
Відкрита транспортна задача
Умову даної задачі запишемо у вигляді розподільчої таблиці.
Математична модель закритої транспортної задачі має наступний вид
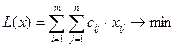
при обмеженнях
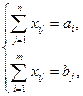
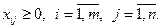
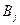
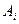
| 
| 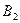
| ... | 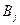
| ... | 
| |
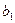
| 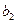
| ... | 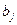
| ... | 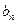
| ||
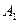
| 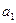
| 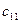
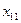
| 

| ... | 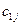
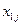
| ... | 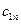
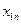
|
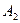
| 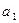
| 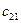
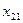
| 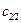
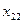
| ... | 
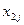
| ... | 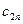

|
| ... | ... | ... | ... | ... | ... | ... | ... |
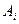
| 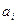
| 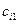
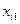
| 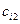
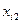
| ... | 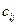

| ... | 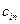

|
| ... | ... | ... | ... | ... | ... | ... | ... |
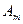
| 
| 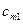
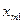
| 
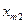
| ... | 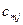
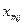
| ... | 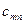

|
Оптимальним розв’язком задачі є матриця 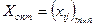 , яка задовольняє системі обмежень і дозволяє мінімізувати цільову функцію.
, яка задовольняє системі обмежень і дозволяє мінімізувати цільову функцію.
Транспортна задача, яка є задачею лінійного програмування, може бути розв’язана симплексним методом, але наявність великої кількості змінних і обмежень робить обчислення громіздкими. Тому для розв’язання транспортних задач розроблено спеціальний метод, який має ті ж самі етапи, що і симплексний метод, а саме:
- знаходження вихідного опорного розв’язку;
- перевірка цього розв’язку на оптимальність;
- перехід від одного опорного розв’язку до іншого.
Знаходження вихідного опорного розв’язку
У розподільчій таблиці клітини, у яких помістимо вантажі, називаються зайнятими і їм відповідають базисні змінні опорного розв’язку. Інші клітини називаються незайнятими або пустими і їм відповідають вільні клітини. У верхньому правому куті кожної клітини будемо записувати тарифи. Існують декілька способів знаходження вихідного опорного розв’язку.
Розглянемо метод мінімального тарифу. Згідно з цим методом, вантажі розподіляються у першу чергу в ті клітини, в яких знаходиться мінімальний тариф перевезень 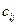 . У подальшому поставки розподіляються у незайнятих клітинах з найменшими тарифами з урахуванням запасів, що залишилися у постачальників, і задоволення попиту споживачів. Процес розподілу продовжують до тих пір, доки всі вантажі від постачальників не будуть вивезеними, а споживачі не будуть задоволеними. При розподілі вантажів може бути, що кількість зайнятих клітин менше, ніж
. У подальшому поставки розподіляються у незайнятих клітинах з найменшими тарифами з урахуванням запасів, що залишилися у постачальників, і задоволення попиту споживачів. Процес розподілу продовжують до тих пір, доки всі вантажі від постачальників не будуть вивезеними, а споживачі не будуть задоволеними. При розподілі вантажів може бути, що кількість зайнятих клітин менше, ніж  . У цьому випадку недостатня їх кількість заповнюється клітинами з нульовими поставками, такі клітини називаються умовно зайнятими.
. У цьому випадку недостатня їх кількість заповнюється клітинами з нульовими поставками, такі клітини називаються умовно зайнятими.
Нульові поставки розміщують у незайняті клітини з урахуванням найменшого тарифу таким чином, щоб у кожному рядку і стовпці було не менше, ніж по одній зайнятій клітині.
Покращення отриманого опорного плану методом потенціалів
Після завершення першого етапу розв’язку задачі знайдені невідомі можна розбити на дві групи – базисні (зайняті) і вільні.
Представимо цільову функцію наступним чином
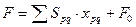 ,
,
де 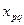 - вільні змінні;
- вільні змінні; 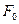 - знайдений опорний план, а значення
- знайдений опорний план, а значення  отримаємо за допомогою методів потенціалів.
отримаємо за допомогою методів потенціалів.
Поставимо у відповідність кожному з пунктів відправлення вантажів 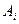 деяку величину
деяку величину 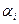 - „потенціал” пункту
- „потенціал” пункту 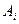 . Аналогічно кожному пункту призначення
. Аналогічно кожному пункту призначення 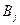 величину
величину 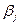 - „потенціалу” пункту
- „потенціалу” пункту 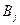 .
.
Для кожного базисного невідомого 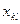 складаємо рівняння
складаємо рівняння 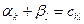 , де
, де 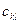 - вартість перевезення з пункту
- вартість перевезення з пункту 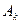 до пункту
до пункту 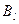 . Розв’язуємо систему рівнянь і знаходимо всі потенціали
. Розв’язуємо систему рівнянь і знаходимо всі потенціали 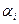 та
та 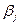 .
.
Тепер для кожної вільної змінної 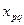 обчислюємо суму
обчислюємо суму  - посередні вартості та заносимо до таблиці.
- посередні вартості та заносимо до таблиці.
Наступним кроком є визначення різниць 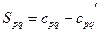 між справжніми вартостями перевезень та посередніми вартостями, які відповідають вільним клітинам.
між справжніми вартостями перевезень та посередніми вартостями, які відповідають вільним клітинам.
Якщо всі величини  невід’ємні, то початковий знайдений розв’язок є оптимальним. Якщо
невід’ємні, то початковий знайдений розв’язок є оптимальним. Якщо 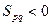 , тоді необхідно перейти до іншого базису.
, тоді необхідно перейти до іншого базису.
Альтернативний оптимум у транспортних задачах
Ознакою наявності альтернативного оптимуму у транспортних задачах є рівність нулю хоча б однієї з оцінок вільних змінних у оптимальному розв’язку 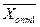 . Зробивши перерозподіл вантажів відносно клітини, що має
. Зробивши перерозподіл вантажів відносно клітини, що має 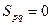 , одержимо новий оптимальний розв’язок
, одержимо новий оптимальний розв’язок 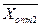 , при цьому значення цільової функції (транспортних витрат) не зміниться.
, при цьому значення цільової функції (транспортних витрат) не зміниться.
Якщо одна різниця дорівнює нулю, тоді оптимальний розв’язок знаходиться за формулою
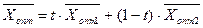 , де
, де 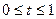 .
.
Виродженість у транспортних задачах
При розв’язанні транспортної задачі може бути, що кількість зайнятих клітин менша за  . У цьому випадку транспортна задача може мати вироджений розв’язок. Для можливого його виключення, доцільно поміняти місцями постачальників і споживачів або ввести у вільну клітину з найменшим тарифом нульову поставку. Нуль вміщують у таку клітину, щоб у кожному рядку і кожному стовпці було не менше однієї зайнятої клітини.
. У цьому випадку транспортна задача може мати вироджений розв’язок. Для можливого його виключення, доцільно поміняти місцями постачальників і споживачів або ввести у вільну клітину з найменшим тарифом нульову поставку. Нуль вміщують у таку клітину, щоб у кожному рядку і кожному стовпці було не менше однієї зайнятої клітини.
Відкрита транспортна задача
При відкритій транспортній задачі сума запасів не співпадає з сумою потреб, тобто 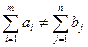 .
.
При цьому:
а). Якщо 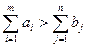 , тоді обсяг запасів перевищує обсяг споживання, всі споживачі будуть задоволені повністю і частина запасів залишається не вивезеною. Для розв’язання такої задачі вводять фіктивного (
, тоді обсяг запасів перевищує обсяг споживання, всі споживачі будуть задоволені повністю і частина запасів залишається не вивезеною. Для розв’язання такої задачі вводять фіктивного (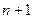 -го) споживача, потреби якого
-го) споживача, потреби якого 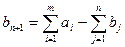 .
.
Модель такої задачі набуває вигляду
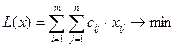
при обмеженнях

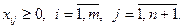
б). Якщо 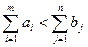 , тоді обсяги споживання перевищують обсяги запасів і частина споживачів залишається незадоволеною. Для розв’язання такої задачі вводять фіктивного (
, тоді обсяги споживання перевищують обсяги запасів і частина споживачів залишається незадоволеною. Для розв’язання такої задачі вводять фіктивного (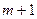 -го) постачальника, обсяги поставок якого
-го) постачальника, обсяги поставок якого 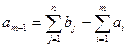 .
.
Модель такої задачі набуває вигляду
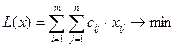
при обмеженнях
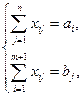
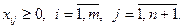
При введенні фіктивного постачальника або споживача, задача стає закритою і розв’язується за раніше розглянутим алгоритмом, причому тарифи, що відповідають фіктивному постачальнику або споживачу більше або дорівнюють найбільшому з усіх тарифів. У цільовій функції фіктивний постачальник або споживач не враховується.
ЦІЛОЧИСЛОВЕ ПРОГРАМУВАННЯ
Загальна постановка задачі
з обмеженнями Оптимальний розв’язок задачі, яку знайдено симплексним методом, часто не є цілочисловим. Його можна округлити до…Метод Гоморі
Метод Гоморі полягає у наступному. Симплексним методом знаходять оптимальний розв’язок задачі. Якщо розв’язок цілочисловий, тоді задача розв’язана.… Нехай одержано оптимальний розв’язок , який не э цілочисловим, тоді останній…Графічний метод
При наявності у задачі лінійного програмування двох змінних, а в системі обмежень – нерівностей, вона може бути розв’язана графічним методом. У системі координат знаходять область припустимих розв’язків (ОПР), будують… У випадку, коли координати цієї точки не є цілочисловими, у ОПР будують цілочислову сітку і знаходять в ній такі цілі…НЕЛІНІЙНЕ ПРОГРАМУВАННЯ
Загальна постановка задачі
Дробово-лінійне програмування
при обмеженнях ,Метод множників Лагранжа
при обмеженнях .Дослідження функції на екстремум за заданою ОПР
- у критичних точках ОПР; - у критичних точках на границях ОПР; - у вершинах ОПРДИНАМІЧНЕ ПРОГРАМУВАННЯ
Загальна постановка задачі
Динамічне програмування – один із розділів оптимального програмування, у якому процес прийняття рішення і управління може бути розбитий на окремі… Економічний процес є керованим, якщо можна впливати на хід його розвитку. Під… Наприклад: випуск продукції є керованим процесом, тому що за управління можна прийняти сукупність рішень (початок…Оптимальна стратегія заміни обладнання
Проблема своєчасної заміни застарілого обладнання новим – одна із нагальних проблем будь якої сфери виробничої діяльності. З часом обладнання… Розглянемо задачу оптимальної політики ремонту і заміни обладнання у… Цех по поточним і капітальним ремонтам не виробляє товарної продукції, тобто оцінити ефективність його діяльності…Оптимальний розподіл ресурсів
Нехай керівництво підприємства розглядає пропозицію про вкладання коштів у п структурних підрозділів. Запропоновано вкласти Х коштів у ці напрямки… Позначимо через - кількість коштів, що виділяються і-тому структурному… Сформульовану задачу можна записати у математичній формі ,Оптимізаційна модель управління товарними запасами
Для побудови економіко-математичної моделі, введемо наступні змінні: - випуск товарної продукції протягом часу ; - рівень запасів на кінець часу .… Вважається, що для кожного періоду витрати залежать від випуску продукції ,…КОНТРОЛЬНІ ЗАВДАННЯ
Задача 2. Розв’язати задачу за допомогою симплексного методу 1. 2. 3. 4. 5. … Задача 3.Знайти оптимальний план перевезень вантажу (- номер варіанта)ЗРАЗКИ РОЗВ’ЯЗАННЯ ЗАДАЧ
Задача 1.
Підприємство виробляє два види продукції. Для виготовлення першого виду продукції використовують два види ресурсів: сировина і електроенергія, витрати яких на одиницю продукції і місячні запаси наведено у таблиці.
| Вихідний ресурс | Витрати вихідного ресурсу на одиницю продукції, грн. | Запаси, грн. | |
| І вид | ІІ вид | ||
| Сировина | 0,8 | 0,5 | |
| Електроенергія | 0,4 | 0,8 |
Вивчення ринку збуту показало, що місячний попит на І вид продукції перевищує попит на ІІ вид не більше ніж на 100 кг. Окрім того, встановлено, що попит на І вид продукції не перевищує 350 кг за місяць. Роздрібна ціна одиниці продукції І виду - 16 грн., а ІІ – 14 грн.
Яку кількість кожного виду продукції 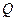 повинно щомісяця виробляти підприємство, щоб виручка
повинно щомісяця виробляти підприємство, щоб виручка  від реалізації продукції була максимальною?
від реалізації продукції була максимальною?
Розв’яжемо задачу за допомогою графічного методу
Позначимо: через 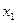 - місячний обсяг випуску продукції І виду, кг; через
- місячний обсяг випуску продукції І виду, кг; через 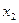 - місячний обсяг випуску продукції ІІ виду, кг.
- місячний обсяг випуску продукції ІІ виду, кг.
Складемо економіко-математичну модель задачі.
За критерій оцінки приймемо виручку від реалізації продукції (В), яка визначається за формулою
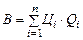 ,
,
де 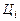 - ціна одиниці і-го виду продукції, грн.;
- ціна одиниці і-го виду продукції, грн.; 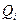 - обсяги виробленої продукції, кг.
- обсяги виробленої продукції, кг.
Цільова функція буде мати вигляд
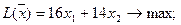
при обмеженнях
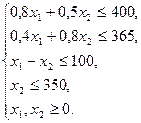
Знайдемо область припустимих розв’язків.
1. 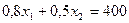 ,
, 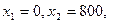

2.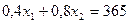 ,
,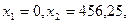
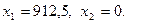
3. 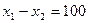 ,
, 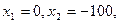
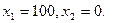
4. 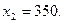
5.  - І чверть.
- І чверть.
Областю припустимих розв’язків є п’ятикутник 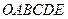 .
.
Для знаходження екстремальних значень цільової функції при графічному розв’язку знайдемо вектор  , який є градієнтом функції
, який є градієнтом функції 

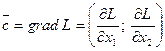 .
.

Проводимо лінію рівня  , яка є перпендикулярною до вектора
, яка є перпендикулярною до вектора  . Оскільки цільова функція досліджується на максимум, то переміщується лінія рівня за напрямком вектора
. Оскільки цільова функція досліджується на максимум, то переміщується лінія рівня за напрямком вектора  . Точкою виходу з області припустимих значень є точка
. Точкою виходу з області припустимих значень є точка 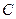 , координати якої визначаються як перетин прямих
, координати якої визначаються як перетин прямих 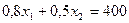 та
та 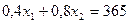 . Розв’язком системи є значення
. Розв’язком системи є значення 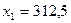 кг і
кг і 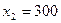 кг.
кг.
Таким чином, найбільше значення функції або максимальна виручка від реалізації продукції складе
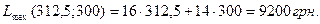
Задача №2
Підприємство виробляє три види продукції. Для виготовлення кожного виду продукції використовують два види ресурсів: сировина і електроенергія, витрати яких на одиницю продукції і місячні запаси наведено у таблиці.
| Вихідний ресурс | Витрати вихідного ресурсу на одиницю продукції, тис. грн. | Запаси, тис. грн. | ||
| І вид | ІІ вид | ІІІ вид | ||
| Сировина | ||||
| Електроенергія |
Роздрібна ціна одиниці продукції І виду - 3 тис. грн., ІІ виду – 4 тис. грн., ІІІ виду – 2 тис. грн.
Яку кількість кожного виду продукції 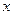 повинно щомісяця виробляти підприємство, щоб виручка
повинно щомісяця виробляти підприємство, щоб виручка  від реалізації продукції був максимальним?
від реалізації продукції був максимальним?
Розв’яжемо задачу за допомогою симплексного методу
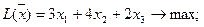
при обмеженнях
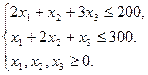
Переведемо економіко-математичну модель до канонічного вигляду
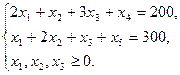
Складемо симплексну таблицю першого кроку

| БЗ | 
| |||||
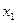
| 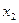
| 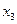
| 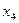
| 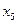
| |||
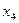
| |||||||
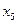
| 2 | ||||||

| -3 | -4 | -2 |
Заповнимо індексний рядок для змінних за формулами
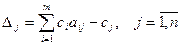
і для вільного члена
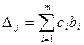 .
.
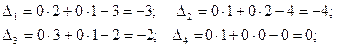
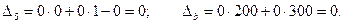
Оскільки, маємо від’ємні оцінки 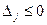 при умові, що цільова функція
при умові, що цільова функція 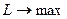 , то знайдений розв’язок не є оптимальним. Складемо симплексну таблицю другого кроку.
, то знайдений розв’язок не є оптимальним. Складемо симплексну таблицю другого кроку.
За ключовий стовпець обираємо четвертий стовпець, який відповідає найменшому значенню індексної оцінки -4, а за індексний елемент 2, тому що найменше значення відношення вільного члена до відповідного елемента ключового стовпця 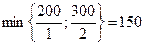 .
.

| БЗ | 
| |||||
| 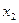
| 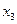
| 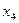
| 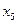
| |||
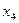
| 
| 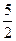
| 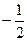
| ||||
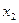
| 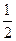
| 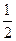
| 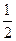
| ||||

| -1 |
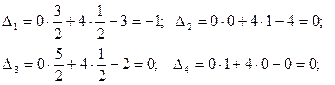
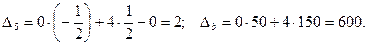 Оскільки, маємо від’ємну оцінку
Оскільки, маємо від’ємну оцінку 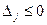 при умові, що цільова функція
при умові, що цільова функція 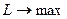 , то знайдений розв’язок не є оптимальним. Складемо симплексну таблицю третього кроку.
, то знайдений розв’язок не є оптимальним. Складемо симплексну таблицю третього кроку.
За ключовий стовпець обираємо третій стовпець, який відповідає від’ємному значенню індексної оцінки -1, а за індексний елемент  , тому що найменше значення відношення вільного члена до відповідного елемента ключового стовпця
, тому що найменше значення відношення вільного члена до відповідного елемента ключового стовпця 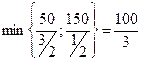 .
.

| БЗ | 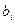
| |||||
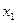
| 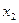
| 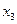
| 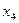
| 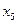
| |||
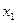
| 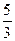
| 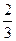
| 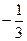
| 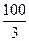
| |||
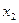
| 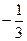
| 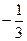
| 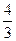
| 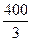
| |||

| 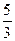
| 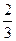
| 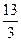
| 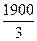
|
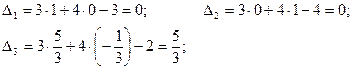
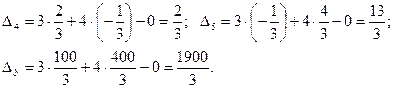
Оскільки, всі оцінки 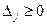 при умові, що цільова функція
при умові, що цільова функція 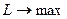 , то знайдений розв’язок є оптимальним.
, то знайдений розв’язок є оптимальним.
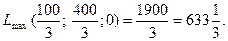
Таким чином, підприємству необхідно виробляти продукцію І і ІІ виду, а випуск продукції ІІІ виду припинити.
Задача №3
На складах 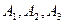 зосереджені запаси продукції у кількості 90, 400, 110 тон відповідно. Споживачі
зосереджені запаси продукції у кількості 90, 400, 110 тон відповідно. Споживачі 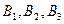 повинні одержати цю продукцію у кількості 140, 300, 160 тон відповідно. Знайти такий варіант закріплення постачальників до споживачів, при якому сума витрат на перевезення була б мінімальною.
повинні одержати цю продукцію у кількості 140, 300, 160 тон відповідно. Знайти такий варіант закріплення постачальників до споживачів, при якому сума витрат на перевезення була б мінімальною.
Витрати на перевезення однієї тони продукції задано матрицею 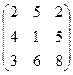 .
.
Перевіримо, чи є дана задача закритою.
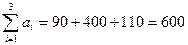 тон;
тон;
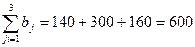 тон.
тон.
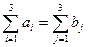 .
.
Отже, дана транспортна задача є закритою.
Знайдемо вихідний опорний розв’язок методом мінімального тарифу.
Кількість зайнятих клітин дорівнює 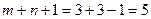 . Умова невиродженості виконана, тому одержуємо опорний розв’язок, який запишемо у вигляді матриці
. Умова невиродженості виконана, тому одержуємо опорний розв’язок, який запишемо у вигляді матриці
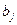
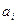
| 
| 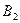
| 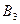
| |
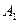
| ||||
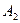
| ||||
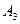
|
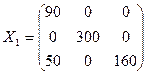 .
.
Вартість перевезень при вихідному опорному розв’язку складає 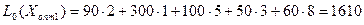 (грн.).
(грн.).
Перевіримо одержаний розв’язок на оптимальність, для цього знайдемо потенціали зайнятих клітин.
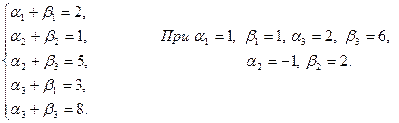
Для вільних клітин знайдемо посередні вартості
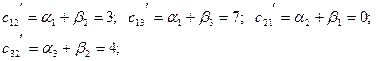
Занесемо результати обчислень до таблиці. Знайдемо різниці між тарифами та посередніми вартостями
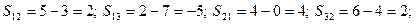 Оскільки серед
Оскільки серед  є від’ємне значення, то знайдений розв’язок не є оптимальним і його необхідно покращити. Перейдемо до нового базису за допомогою циклу перерахунку. Для цього представимо функцію у вигляді
є від’ємне значення, то знайдений розв’язок не є оптимальним і його необхідно покращити. Перейдемо до нового базису за допомогою циклу перерахунку. Для цього представимо функцію у вигляді
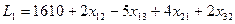
Маємо один від’ємний коефіцієнт  , тому при його збільшенні функція
, тому при його збільшенні функція 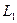 буде зменшуватися. Покладемо
буде зменшуватися. Покладемо 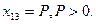 Пересуваємо вантаж
Пересуваємо вантаж  по таблиці
по таблиці 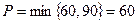 .
.
Одержуємо новий план, який представлений у таблиці.
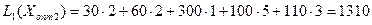 .
.
Перевіримо новий план на оптимальність. Для цього повторимо повний цикл розрахунків.
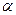
| 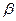
| ||
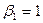
| 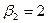
| 
| |
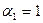
|   2
90 -Р 2
90 -Р
| 5 | 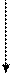 2
7 +Р 2
7 +Р
|
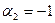
| 4 | ||
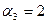
|  3
50 +Р 3
50 +Р
| 6 | 60 -Р |
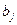
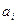
| 
| 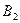
| 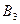
| |
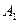
| ||||
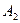
| ||||
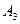
|
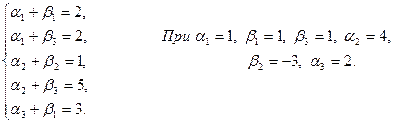
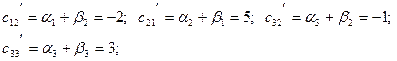
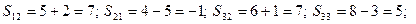 Представимо функцію у вигляді
Представимо функцію у вигляді

Перейдемо до нового базису
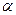
| 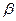
| ||
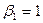
| 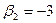
| 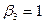
| |
|   2
30 -Р 2
30 -Р
| 5 -2 |  2
60 +Р 2
60 +Р
|
| 4
 5 +Р 5 +Р
| 100 -Р | |
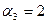
| 6 -1 | 8 3 |
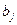
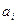
| 
| 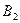
| 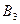
| |
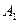
| ||||
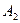
| ||||
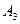
|
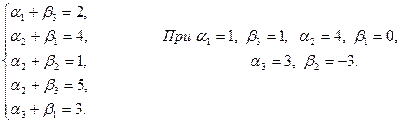
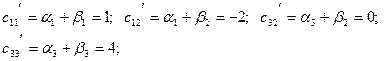
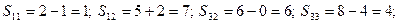
Оскільки серед  немає від’ємних значень, то знайдений розв’язок є оптимальним.
немає від’ємних значень, то знайдений розв’язок є оптимальним.
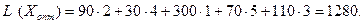
Задача №4
Для покращення фінансового стану підприємство прийняло рішення про збільшення випуску конкурентноздатної продукції, для чого було вирішено встановити у одному із цехів додаткового обладнання, яке займає 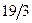 м2 площі. На придбання додаткового обладнання підприємство виділило 10 тис. грн., при цьому воно може придбати обладнання двох видів. Придбання одного комплекту обладнання 1-го виду коштує 1 тис. грн., 2-го виду – 3 тис. грн. Придбання одного комплекту обладнання 1-го виду дозволяє збільшити випуск продукції за зміну на 2 шт., а одного комплекту 2-го виду – на 4 шт. Враховуючи, що для встановлення одного комплекту 1-го виду необхідно 1 м2 площі, а для обладнання 2-го виду – 1 м2 площі. Визначити такий набір додаткового обладнання, який дає можливість максимально збільшити випуск продукції.
м2 площі. На придбання додаткового обладнання підприємство виділило 10 тис. грн., при цьому воно може придбати обладнання двох видів. Придбання одного комплекту обладнання 1-го виду коштує 1 тис. грн., 2-го виду – 3 тис. грн. Придбання одного комплекту обладнання 1-го виду дозволяє збільшити випуск продукції за зміну на 2 шт., а одного комплекту 2-го виду – на 4 шт. Враховуючи, що для встановлення одного комплекту 1-го виду необхідно 1 м2 площі, а для обладнання 2-го виду – 1 м2 площі. Визначити такий набір додаткового обладнання, який дає можливість максимально збільшити випуск продукції.
Припустима, що підприємство придбало 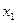 комплектів додаткового обладнання 1-го виду і
комплектів додаткового обладнання 1-го виду і 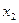 комплектів обладнання 2-го виду.
комплектів обладнання 2-го виду.
Цільова функція має вигляд

із обмеженнями 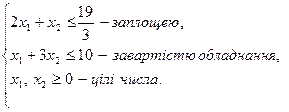
Розв’яжемо задачу методом Гоморі
Спочатку розв’яжемо симплексним методом, для цього перейдемо до канонічної форми системи обмежень
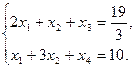
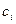
| БЗ | 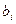
| ||||
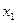
| 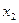
| 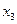
| 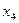
| |||
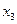
| 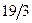
| |||||
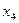
| 3 | |||||

| -2 | -4 |
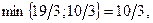
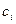
| БЗ | 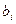
| ||||
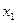
| 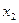
| 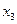
| 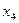
| |||
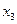
| 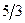
| 
| ||||
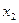
| 
| 
| 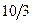
| |||

| 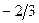
| 
| 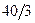
|

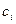
| БЗ | 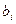
| ||||
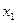
| 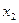
| 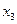
| 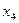
| |||
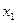
| 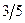
| 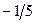
| 
| |||
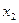
| 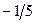
| 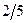
| 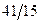
| |||

| 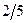
| 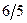
| 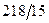
|
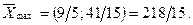
Знайдемо дробові частини чисел
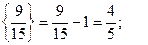

Порівняємо

Враховуючи дробові частини чисел 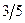 і
і 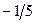
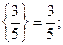
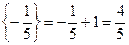 складемо додаткові обмеження цілочислові для першого рядка
складемо додаткові обмеження цілочислові для першого рядка 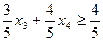 або
або 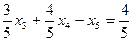 і введемо додатковий рядок таблиці
і введемо додатковий рядок таблиці
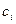
| БЗ | 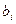
| |||||
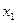
| 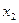
| 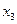
| 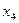
| 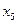
| |||
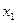
| 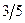
| 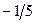
| 
| ||||
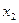
| 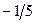
| 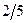
| 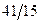
| ||||
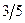
| 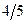
| -1 | 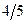
|
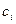
| БЗ | 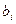
| |||||
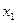
| 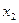
| 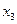
| 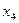
| 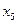
| |||
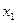
| -1 | ||||||
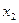
| 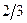
| 
| 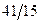
| ||||
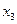
| 
| 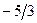
| 
| ||||

| 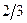
| 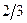
|

Графічний метод
Областю припустимих розв’язків є чотирьохкутник ОАВС, а 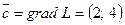 .
.
Оптимальний розв’язок задача має у точці В
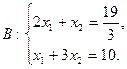
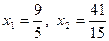 .
.
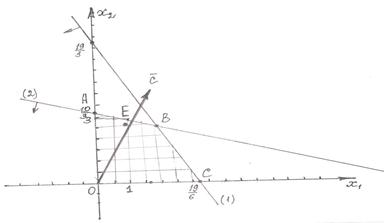
Одержане оптимальне значення не є цілочисловим. Замінимо багатокутник ОАВС на ОКЕМNF. Лінія рівня переміщується у точку 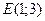 де і є максимальне значення цільової функції
де і є максимальне значення цільової функції 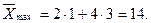
Таким чином, підприємству необхідно придбати 1 комплект обладнання першого виду і 3 комплекти обладнання другого виду, що забезпечить йому при наявних обмеженнях на виробничі площі і грошові кошти максимальне збільшення випуску продукції, яке дорівнює 14 тис. грн. за зміну.
Задача 5
Дослідити функцію на екстремум
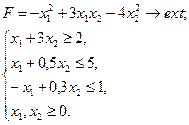
- Побудуємо область обмежень
1. 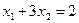
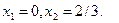
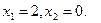
2. 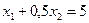
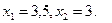
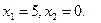
3. 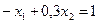
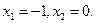
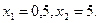
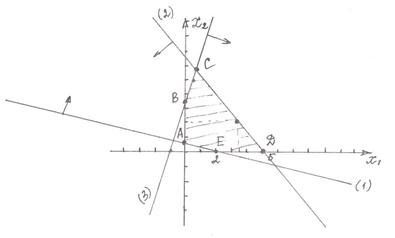
Областю обмежень є множина точок площини ХОУ, що належать чотирьохкутнику АВСDE з вершинами:
А (0; 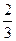 ); В(
); В(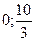 ); С(1,25; 7,5); D(5; 0); E(2; 0)
); С(1,25; 7,5); D(5; 0); E(2; 0)
- Знайдемо значення функції у критичних точках області
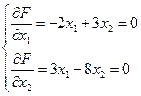
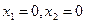
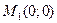 - критична точка, що не належить області розв’язків.
- критична точка, що не належить області розв’язків.
- Знайдемо значення функції у критичних точках на границях області.
1) 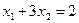 ;
; 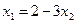

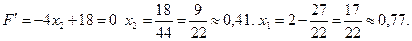
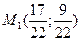 - критична точка, що належить області розв’язків.
- критична точка, що належить області розв’язків.
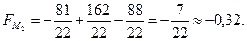
2) 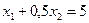 ;
; 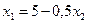 .
.
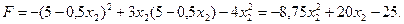
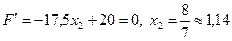
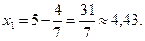 Критична точка
Критична точка  належить області розв’язків, тому
належить області розв’язків, тому 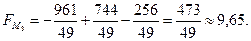
3) 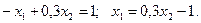
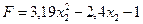 ;
; 
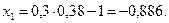 Критична точка не належить області розв’язків.
Критична точка не належить області розв’язків.
4. Знайдемо значення функції у вершинах області розв’язків
А (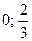 ); В(
); В(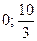 ); С(1,25; 7,5); D(5; 0); E(2; 0)
); С(1,25; 7,5); D(5; 0); E(2; 0)

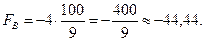
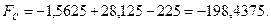
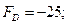
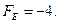
Значить: 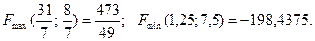
Задача 6
Гірничо-збагачувальний комбінат виробляє товарну продукцію – концентрат, який реалізує на внутрішній і зовнішній ринки збуту. При продажу 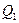 тон концентрату на внутрішній ринок витрати на реалізацію складають
тон концентрату на внутрішній ринок витрати на реалізацію складають 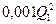 грн., а при продажу
грн., а при продажу 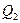 тон концентрату на зовнішній ринок -
тон концентрату на зовнішній ринок -  грн.
грн.
Визначити, яку кількість концентрату (тон) необхідно продавати на внутрішній і зовнішній ринки, щоб витрати на реалізацію були мінімальними, якщо за рік реалізується 10000 тис. тон концентрату.
Розв’яжемо задачу за допомогою методу множників Лагранжа
Складемо економіко-математичну модель задачі. Цільова функція економіко-математичної моделі має вигляд
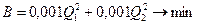 ,
,
де  - витрати на реалізацію концентрату, грн.
- витрати на реалізацію концентрату, грн.
при обмеженнях

Складемо функцію Лагранжа
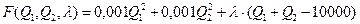 .
.
За необхідною умовою існування екстремуму функції, знайдемо частинні похідні функції 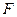 за змінними
за змінними 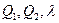 , прирівняємо їх до нуля та одержимо систему рівнянь
, прирівняємо їх до нуля та одержимо систему рівнянь
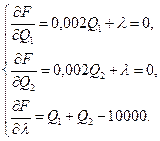
Після елементарних перетворень одержуємо
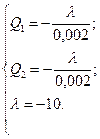
Звідки  тис. тон;
тис. тон;  тис. тон.
тис. тон.
Перевіримо одержані значення на оптимальність. Використаємо достатню умову екстремуму функції двох змінних.
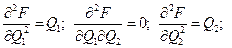
Одержуємо, 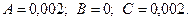 Звідси,
Звідси, 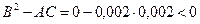 , тому у точці (5000; 5000) існує екстремум функції. При
, тому у точці (5000; 5000) існує екстремум функції. При 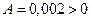 одержуємо, що у досліджуваній точці існує мінімум функції, значить, мінімальні витрати на реалізацію концентрату дорівнюють
одержуємо, що у досліджуваній точці існує мінімум функції, значить, мінімальні витрати на реалізацію концентрату дорівнюють
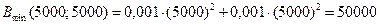 грн.
грн.
Задача 7
Для виробництва двох видів продукції виробів А і В підприємство використовує три типи технологічного обладнання. Кожен із виробів повинен пройти обробку на кожному з типів обладнання. Час обробки кожного з виробів, витрати, що пов’язані з виробництвом одного виробу, задано у таблиці
| Тип обладнання | Витрати часу на обробку одного виробу, час. | |
| А | В | |
| І | ||
| ІІ | ||
| ІІІ | ||
| Витрати на виробництво одного виробу, тис. грн. |
Обладнання І і ІІІ типів підприємство може використовувати не більше 26 і 39 годин відповідно, обладнання ІІ типу доцільно використовувати не менше 4 год.
Визначити, скільки виробів кожного виду треба виробити підприємству, щоб середня собівартість одного виробу була мінімальною.
Позначимо 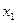 - кількість виробів виду А;
- кількість виробів виду А; 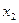 - кількість виробів виду В. Загальні витрати на їх виробництво складають
- кількість виробів виду В. Загальні витрати на їх виробництво складають 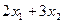 тис. грн., а середня собівартість одного виробу дорівнює
тис. грн., а середня собівартість одного виробу дорівнює 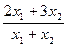 , тому математична модель задачі має вигляд
, тому математична модель задачі має вигляд
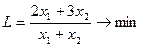
при обмеженнях
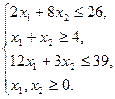
Побудуємо область припустимих розв’язків – трикутник АВС.
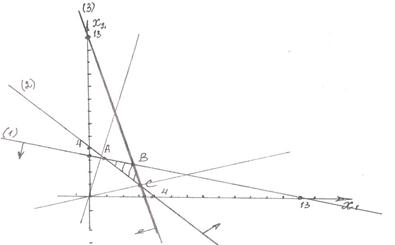
Із цільової функції виразимо 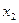

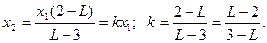
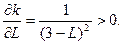
Значить кутовий коефіцієнт прямої 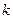 зростає, тобто пряма обертається проти годинникової стрілки і у точці С є мінімум, а у точці А – максимум.
зростає, тобто пряма обертається проти годинникової стрілки і у точці С є мінімум, а у точці А – максимум.
Знайдемо координати точки С
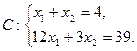
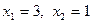 .
.
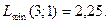
Тому підприємство повинно випускати 3 вироби виду А і 1 виріб виду В, при цьому середня собівартість буде складати 2,25 грн.
Задача №8
Наведена таблиця міжгалузевих зв’язків для 3 галузей промисловості. Необхідно визначити обсяги випуску продукції кожної галузі, якщо кінцевий продукт буде змінюватися і дорівнювати відповідно 40, 30 і 50 млн. грн.
| Галузь промисловості | Обсяг продукції, млн. грн. | Міжгалузеві потоки в галузях, млн. грн. | ||
| №1 | №2 | №3 | ||
Для розв’язання застосуємо задачу про складання міжгалузевого балансу Леонтьєва
Складемо матрицю технології виробництва, використовуючи формулу
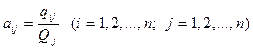 .
.

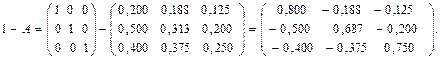
Знайдемо матрицю 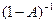 , обернену до матриці (
, обернену до матриці (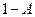 ), визначник якої
), визначник якої
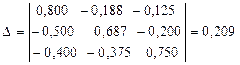 .
.
Знайдемо алгебраїчні доповнення до елементів матриці (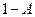 ):
):
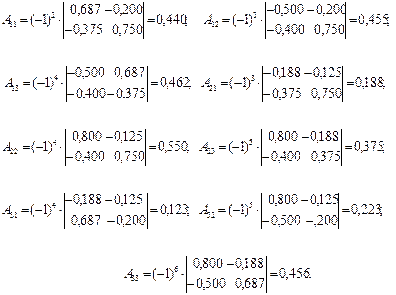
Тоді матриця коефіцієнтів сумісного споживання має вигляд

Обсяги продукції, які необхідно виробляти кожній галузі будуть дорівнювати
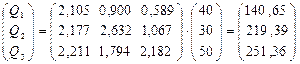
Таким чином, випуск продукції в першій галузі необхідно зменшити до 140,65 млн. грн., у другій – до 219,39 млн. грн., а у третій – до 251,36 млн. грн.
Задача 9
Міністерство розглядає пропозицію щодо нарощення виробничих потужностей для збільшення випуску однорідної продукції на чотирьох підприємствах, що належать даній галузі.
Для розширення виробництва міністерство виділяє кошти у обсязі 120 млн. грн. з дискретністю 20 млн. грн. Приріст випуску продукції на підприємствах залежить від суми виділених коштів, значення якого представлені у таблиці.
| Кошти, млн. грн. | Приріст випуску продукції, млн. грн. | |||
| Підприємство №1 | Підприємство №2 | Підприємство №3 | Підприємство №4 | |
Знайти розподіл коштів між підприємствами, що забезпечує максимальний приріст випуску продукції, причому на одне підприємство може виділятися не більше однієї інвестиції.
Розв’яжемо задачу за допомогою методу динамічного програмування
Розіб’ємо розв’язок задачі на чотири етапи за кількістю підприємств, на які передбачається здійснити інвестиції.
Рекурентне співвідношення буде мати вигляд:
- для підприємства №1
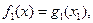
- для всіх інших підприємств
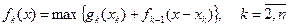 .
.
Розв’язок будемо виконувати у відповідності до рекурентних співвідношень у чотири етапи.
1 етап.
Інвестиції надаємо тільки першому підприємству. Тоді:
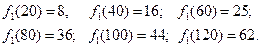
2 етап.
Інвестиції виділяємо першому і другому підприємствам. Рекурентне співвідношення для другого етапу має вигляд
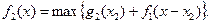
Тоді при 
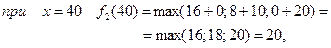
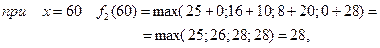

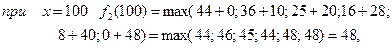
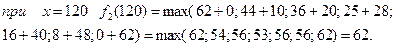
3 етап.
Фінансуємо другий етап і третє підприємство. Розрахунки виконуємо за формулою
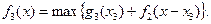
Тоді:
при 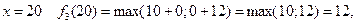
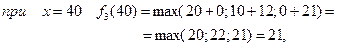
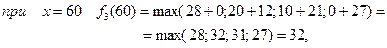
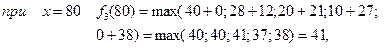
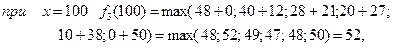

4 етап.
Інвестиції розміром 120 млн. грн. розподіляємо між третім етапом і четвертим підприємством
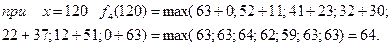
Одержано умови управління від першого до четвертого етапу. Повернемося від четвертого до першого етапу. Максимальний приріст випуску продукції у 64 млн. грн. одержано на четвертому етапі як 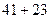 , тобто 23 млн. грн. відповідають виділенню 40 млн. грн. четвертому підприємству (див. табл.). Відповідно до третього етапу 41 млн. грн. одержано як
, тобто 23 млн. грн. відповідають виділенню 40 млн. грн. четвертому підприємству (див. табл.). Відповідно до третього етапу 41 млн. грн. одержано як 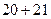 , тобто 21 млн. грн. відповідає виділенню 40 млн. грн. третьому підприємству. Відповідно до другого етапу, 20 млн. грн. одержано при виділенні 40 млн. грн. другому підприємству.
, тобто 21 млн. грн. відповідає виділенню 40 млн. грн. третьому підприємству. Відповідно до другого етапу, 20 млн. грн. одержано при виділенні 40 млн. грн. другому підприємству.
Таким чином, інвестиції обсягом 120 млн. грн. доцільно виділяти другому, третьому і четвертому підприємствам по 40 млн. грн., при цьому максимальний приріст продукції складе 64 млн. грн.
Список використаних джерел
1. Вітлінський В.В. Моделювання економіки: Навч. посібник. – 2-ге вид., без змін. – К.: КНЕУ, 2007. – 408 с. 2. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом… 3. Гришин А.Ф., Кочерова Е.В. Статистические модели: построение, оценка, анализ: Учеб. пособие. - М.: Финансы и…– Конец работы –
Используемые теги: ЛІНІЙНЕ, програмування, транспортна, Задача, ЦІЛОЧИСЛОВЕ, програмування0.087
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ЛІНІЙНЕ ПРОГРАМУВАННЯ. Транспортна задача. ЦІЛОЧИСЛОВЕ ПРОГРАМУВАННЯ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов