рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Спорт
- /
- Оптимальна стратегія заміни обладнання
Реферат Курсовая Конспект
Оптимальна стратегія заміни обладнання
Оптимальна стратегія заміни обладнання - раздел Спорт, ЛІНІЙНЕ ПРОГРАМУВАННЯ. Транспортна задача. ЦІЛОЧИСЛОВЕ ПРОГРАМУВАННЯ Проблема Своєчасної Заміни Застарілого Обладнання Но...
Проблема своєчасної заміни застарілого обладнання новим – одна із нагальних проблем будь якої сфери виробничої діяльності. З часом обладнання зношується і фізично і морально, тому на кожному етапі його експлуатація стає менш вигідною у порівнянні з придбанням і використанням нового обладнання. У зв’язку з цим і виникає задача визначення найбільш доцільного моменту заміни. За критерій оптимальності при заміні обладнання у промисловості звичайно приймають мінімум очікуваних витрат або максимум очікуваного прибутку за деякий період часу.
Розглянемо задачу оптимальної політики ремонту і заміни обладнання у спрощеному вигляді. Нехай на початку планового періоду із 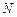 років маємо деяке обладнання віком
років маємо деяке обладнання віком 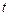 . Кожний рік виробляється продукція, витрати на виробництво якої складають
. Кожний рік виробляється продукція, витрати на виробництво якої складають  . При цьому обладнання вимагає експлуатаційних (поточних) витрат
. При цьому обладнання вимагає експлуатаційних (поточних) витрат  і має залишкову вартість
і має залишкову вартість 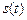 . Всі перелічені характеристики залежать від віку
. Всі перелічені характеристики залежать від віку 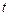 обладнання. У будь який рік обладнання можна зберігати або продати за залишковою вартістю і купити нове за ціною
обладнання. У будь який рік обладнання можна зберігати або продати за залишковою вартістю і купити нове за ціною 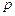 . Сюди входять витрати на установку і запуск в експлуатацію.
. Сюди входять витрати на установку і запуск в експлуатацію.
Цех по поточним і капітальним ремонтам не виробляє товарної продукції, тобто оцінити ефективність його діяльності неможливо за одержаним прибутком. Тому необхідно розробити оптимальну політику заміни обладнання виходячи з умов мінімізації очікуваних витрат за період часу довжиною 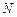 років.
років.
У відповідності з загальною концепцією динамічного програмування почнемо процес оптимізації від кінця планового періоду. При цьому роки будуть нумеруватися від кінця періоду до його початку: 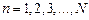 .
.
Нехай 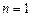 . Будемо вважати, що до початку останнього року у нас є в наявності обладнання віком
. Будемо вважати, що до початку останнього року у нас є в наявності обладнання віком 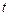 років. За нашим вибором буде прийняте одне з наступних рішень: зберігати обладнання або продати його і придбати взамін нове.
років. За нашим вибором буде прийняте одне з наступних рішень: зберігати обладнання або продати його і придбати взамін нове.
Якщо ми приймаємо рішення зберігати обладнання, тоді за останній рік витрати складуть
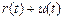
Якщо ж обладнання продати по залишковій вартості і купити нове, тоді витрати до кінця останнього року складуть
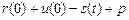 , де
, де 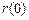 - витрати на виробництво продукції на новому обладнанні, тобто нульового віку за рік;
- витрати на виробництво продукції на новому обладнанні, тобто нульового віку за рік; 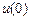 - витрати, що пов’язані з експлуатацією нового обладнання протягом року.
- витрати, що пов’язані з експлуатацією нового обладнання протягом року.
Оскільки планується діяльність за останній рік планового періоду, то у відповідності з концепцією динамічного програмування ми повинні діяти так, щоб останній рік сам по собі приніс мінімум витрат. Але результати діяльності у даному випадку характеризуються виразами 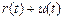 і
і 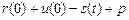 . Замінити обладнання буде вигідно, якщо
. Замінити обладнання буде вигідно, якщо  , тобто коли сумарні витрати при роботі на новому обладнанні будуть менше, ніж при роботі на старому.
, тобто коли сумарні витрати при роботі на новому обладнанні будуть менше, ніж при роботі на старому.
Позначимо через 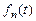 мінімально можливі сумарні витрати за останні
мінімально можливі сумарні витрати за останні 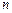 років планового періоду при умові, що на початку періоду маємо обладнання віком
років планового періоду при умові, що на початку періоду маємо обладнання віком 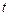 і ми дотримуємся оптимальної політики. У відповідності з цим мінімальні витрати за останній рік позначимо через
і ми дотримуємся оптимальної політики. У відповідності з цим мінімальні витрати за останній рік позначимо через 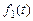 . Зрозуміло, що
. Зрозуміло, що 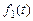 дорівнює найменшому з виразів
дорівнює найменшому з виразів 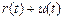 і
і 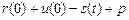 , що символічно можна записати у вигляді
, що символічно можна записати у вигляді
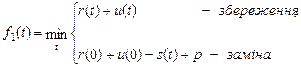
Нехай 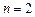 , тобто розглянемо період, який складається з двох останніх років.
, тобто розглянемо період, який складається з двох останніх років.
Якщо до початку цього періоду у наявності є обладнання віком 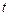 і прийнято рішення його зберігати, тоді в кінці першого року величина сумарних витрат дорівнює
і прийнято рішення його зберігати, тоді в кінці першого року величина сумарних витрат дорівнює 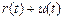 . За рік обладнання стане старшим на рік і до кінця першого року буде мати вік (
. За рік обладнання стане старшим на рік і до кінця першого року буде мати вік (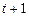 ) рік. Якщо по відношенню до цього обладнання в останній рік дотримуватися оптимальної політики, тоді додатково будуть одержані сумарні витрати
) рік. Якщо по відношенню до цього обладнання в останній рік дотримуватися оптимальної політики, тоді додатково будуть одержані сумарні витрати  , а загальні витрати за два роки складуть
, а загальні витрати за два роки складуть
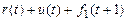 .
.
Якщо ж на початку другого року буде прийняти рішення про заміну обладнання, тоді витрати, що пов’язані з реалізацією старого обладнання і придбанням нового, складуть  , а сумарні витрати на нове обладнання за перший рік будуть дорівнювати
, а сумарні витрати на нове обладнання за перший рік будуть дорівнювати 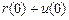 . До кінця року нове обладнання постаріє і буде мати вік один рік, тому оптимальна політика в останньому році виражається через витрати
. До кінця року нове обладнання постаріє і буде мати вік один рік, тому оптимальна політика в останньому році виражається через витрати 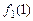 .
.
Загальні витрати за два роки складуть
 .
.
Оптимальною за два останні роки буде політика, яка забезпечує за цей період мінімальні загальні витрати, які дорівнюють найменшому з виразів. Записати це можна у вигляді
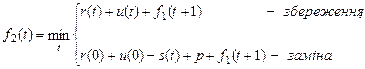
Аналогічно одержуємо вираз для 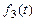 і т.д. Загальне функціональне рівняння Белмана має вигляд
і т.д. Загальне функціональне рівняння Белмана має вигляд
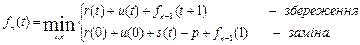 ,
,
де п=2, 3,...; t=0, 1, 2, …
Рекурентні співвідношення дозволяють реалізувати концепцію динамічного програмування і розгорнути процес формування оптимальної політики заміни обладнання з кінця періоду, що планується, послідовно відшукуючи  для різних значень
для різних значень 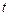 .
.
– Конец работы –
Эта тема принадлежит разделу:
ЛІНІЙНЕ ПРОГРАМУВАННЯ. Транспортна задача. ЦІЛОЧИСЛОВЕ ПРОГРАМУВАННЯ
Криворізький технічний університет... Кафедра економіки організації та управління підприємствами... МЕТОДИЧНІ ВКАЗІВКИ Кривий Ріг...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Оптимальна стратегія заміни обладнання
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов