рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Военное дело
- /
- МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОТОКА ЗАЯВОК
Реферат Курсовая Конспект
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОТОКА ЗАЯВОК
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОТОКА ЗАЯВОК - раздел Военное дело, По учебной дисциплине Телефония и военные коммутационные системы Потребности S Абонентов В Передаче Сообщений По Определенным Адресам Проявляе...
Потребности S абонентов в передаче сообщений по определенным адресам проявляется в потоке заявок (вызовов телефонной станции) на установление соединений в заданных направлениях. Будем полагать, что заявки на обслуживание поступают последовательно во времени. Таким образом, поток заявок есть последовательность одноразовых событий (вызовов абонентами телефонной станции), заключающихся в появлении одна за другой на входе СМО (телефонной станции) заявок на обслуживание в случайные моменты времени. Случайность потока заявок обусловлена тем, что источники информации полагаются независимыми и потребность в установлении соединения для каждого абонента сети возникает в результате трудно прогнозируемых факторов.
На временной оси t поток заявок можно изобразить последовательностью точек t1, t2, t3,..., соответствующих моментам их появления.
Выберем такую модель потока заявок, которая обладала бы особо простыми свойствами, но, в то же время, достаточно адекватно отражала реальную действительность. Особо простыми свойствами модели потока заявок можно считать следующие: стационарность, ординарность и отсутствие последействия.
Свойство стационарности означает, что вероятность попадания того или иного числа заявок на интервал времени t зависит только от длины этого интервала и не зависит от его расположения на оси времени. На практике это свойство может иметь место только на ограниченном участке времени, так как очевидно, что число вызовов, поступающих на телефонную станцию, существенно зависит от времени суток.
Свойство ординарности означает, что вероятность попадания на элементарный участок времени t двух и более заявок пренебрежимо мала по сравнению с вероятностью попадания одной заявки. Иными словами, заявки на обслуживание не могут приходить двойными, тройными и т.д.
Свойство отсутствия последействия в телефонии означает на практике, что для любых неперекрывающихся временных интервалов число заявок, попадающих на один из них, не зависит от числа заявок, попадающих на другие интервалы.
Условие отсутствия последействия наиболее существенное из всех и предполагает, что заявки на установление соединения того или иного абонента обусловлены причинами, совершенно не связанными с причинами потребности в установлении соединений для других абонентов.
Случайный поток сообщений, обладающий свойствами стационарности, ординарности и отсутствия последействия, называется простейшим или стационарным пуассоновским потоком.
Модель простейшего потока заявок широко используется при анализе СМО. Дело в том, что при суммировании большого числа (а на практике достаточно сложить 4-5 потоков) ординарных, стационарных с практически любым последействием потоков получается результирующий поток заявок, сколь угодно близкий к простейшему.
Задается простейший поток семейством вероятностей Рк(τ) поступления ровно k заявок (вызовов) в промежутке τ :
Рк(ф) =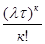 е -
е -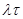 ,
,
где l - параметр потока заявок.
Приведенная выше формула называется в теории телефонии и телетрафика формулой Пуассона по имени французского ученого, впервые предложившего методику численного расчета вероятностно-временных характеристик и параметров СМО подобного типа.
Физический смысл параметра l легко уяснить, если произвести вычисление математического ожидания числа заявок на интервале 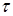 :
:
М[к] = 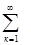 кРк(
кРк(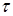 ) =
) = 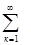 к
к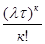 е -
е -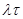 =
=
= е -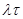
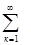
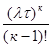 = l
= l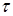 е -
е -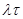
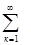
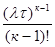 =
= 


 j = к-1
j = к-1
= к = 1; j =0 = l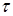 е -
е -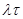
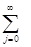
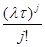 =
=
к = ¥;j= ¥
= l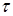 е -
е -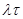 е+
е+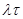 = l
= l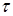 .
.
Из полученного выражения следует, что параметр простейшего потока заявок lесть среднее число заявок, поступивших на вход СМО в единицу времени, то есть имеет размерность [заявок/сек]. Этот параметр называют интенсивностью потока заявок.
Вероятность непоступления ни одной заявки на интервале времени ф следует из формулы Пуассона и равна
Ро(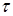 ) =
) = 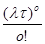 е -
е -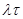 = е -
= е -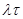 .
.
Если положить интервал времени достаточно малым, то есть l 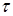 <1, то
<1, то
е -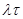
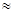 1- l
1- l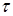 ;Ро(
;Ро(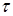 )
) 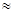 1- l
1- l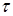 .
.
Вероятность появления хотя бы одного вызова на малом интервале 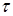 можно найти из выражения Ро(
можно найти из выражения Ро(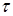 )+ Р1(
)+ Р1(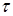 )
) 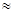 1 , то есть
1 , то есть
– Конец работы –
Эта тема принадлежит разделу:
По учебной дисциплине Телефония и военные коммутационные системы
ВОЕННАЯ АКАДЕМИЯ РЕСПУБЛИКИ БЕЛАРУСЬ... КАФЕДРА СВЯЗИ... УТВЕРЖДАЮ Начальник кафедры...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОТОКА ЗАЯВОК
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов