рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Военное дело
- /
- МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СМО С ПОТЕРЯМИ
Реферат Курсовая Конспект
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СМО С ПОТЕРЯМИ
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СМО С ПОТЕРЯМИ - раздел Военное дело, По учебной дисциплине Телефония и военные коммутационные системы Рассмотрим Коммутационную Систему, В Которой Поступающим Заявкам (Вызовам) До...
Рассмотрим коммутационную систему, в которой поступающим заявкам (вызовам) доступны V обслуживающих приборов. Каждая вновь поступившая заявка подается на свободный обслуживающий прибор (ОП). Однако, если вызов поступает в момент, когда все приборы заняты, то он теряется, то есть получает отказ в обслуживании. Возможны две наиболее типичных ситуации.
1. Рассмотрим ситуацию, когда поток заявок простейший и характеризуется постоянной интенсивностью l=const. Длительность обслуживания заявки подчинена показательному закону распределения с интенсивностью обслуживания m=1/Тобсл.
Граф интенсивностей переходов для системы с V обслуживающими приборами при простейшем потоке заявок показан на рис. 8.1.
Для рассматриваемого случая
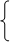 lк = l, к< v
lк = l, к< v
0, к ³ v ;mк = кm; к = 1,…,v.
Вероятность пребывания системы в состоянии Хк
Рк =  ; к £ v,
; к £ v,
или
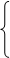 Рк = Ро
Рк = Ро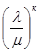
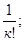 к £ v
к £ v
0, к > v
Ро =  .
.
Таким образом, вероятность того, что в системе занято к обслуживающих приборов или, что то же самое, в системе находится на обслуживании к заявок, равна
Рк =  ,
,
где 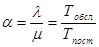 - среднее число заявок, приходящееся на среднее время обслуживания одной заявки.
- среднее число заявок, приходящееся на среднее время обслуживания одной заявки.
Вероятность отказа в обслуживании очередной заявки Ротк = Рv. Вероятность Рv характеризует долю времени, когда все V приборов заняты:
Ротк = Рv = 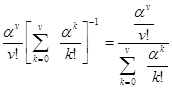
Это выражение позволяет определить потери в обслуживании заявок и называется в телефонии формулой потерь Эрланга (впервые получена Эрлангом в 1917 году).
Формула Эрланга играет большую роль в телефонии и табулирована для различных значений V, , Р. Составлены таблицы, получившие название по фамилии их автора таблиц Пальма. Использование таблиц и построенных с их помощью номограмм позволяет, не прибегая к расчетам и вычислениям вероятностей по формулам, найти один из неизвестных параметров V,
, Р. Составлены таблицы, получившие название по фамилии их автора таблиц Пальма. Использование таблиц и построенных с их помощью номограмм позволяет, не прибегая к расчетам и вычислениям вероятностей по формулам, найти один из неизвестных параметров V,  или Р по двум известным.
или Р по двум известным.
Среднее число занятых обслуживающих приборов определяется как
mk=M ,
,
так как
 Po
Po 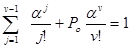
 |
Pобсл Pотк
При неограниченном числе обслуживающих приборов
mk =  ;
;
Po 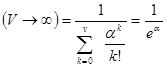 ; mk =
; mk = 
2. Рассмотрим другую ситуацию, когда поток заявок поступает от конечного числа S источников и является примитивным. Тогда
 lk = la (S-k), 0 £ к £ S;
lk = la (S-k), 0 £ к £ S;
0 - в остальных случаях.
Граф интенсивностей переходов для системы с V<S обслуживающими приборами и примитивном потоке заявок приведен на рис. 8.2.
В данном случае интенсивность входного потока учитывает число обслуживающих приборов и равна li = (S-i)la, где i £ V-1.
Если заняты все V приборов, заявка получит отказ в обслуживании.
Вероятность занятия к приборов определяется выражением
Pk = 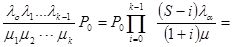
= Po 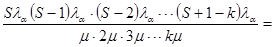
= Po 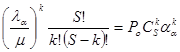 ,
,
где  - число вызовов от одного абонента, приходящееся на среднее время обслуживания заявки или приведенная интенсивность вызовов одного абонента.
- число вызовов от одного абонента, приходящееся на среднее время обслуживания заявки или приведенная интенсивность вызовов одного абонента.
Вероятность непоступления ни одного вызова (незанятия хотя бы одного ОП) рассчитывается по формуле
Po=
Выражение, полученное подстановкой значения Ро в формулу для нахождения Рк, вида
Pк = 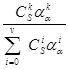 (к=0...V)
(к=0...V)
называют формулой Энгсета, которая, наравне с формулой потерь Эрланга, является одной из основных в теории телетрафика.
Вероятность отказа в обслуживании очередной заявки находится из выражения:
Pотк = 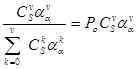 .
.
Среднее число занятых обслуживанием приборов равно
mk = 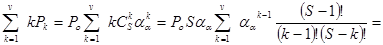

 j = k-1; k = 1® j = 0;
j = k-1; k = 1® j = 0;
= k = v ® j = v-1 = Po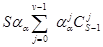
При теоретически бесконечном числе ОП и конечном числе S источников вызовов (нагрузки) граф интенсивностей переходов представлен рис. 8.3.
Для вероятностей Рк этой системы
Pk =  , (0 £ к £ S),
, (0 £ к £ S),
где вероятность Р0 определяется выражением
Po =  .
.
Согласно выражению бинома Ньютона можно записать:

Po =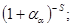
Pk = 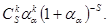
Тогда среднее число занятых обслуживающих приборов равно
mk = 
= 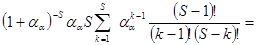
= 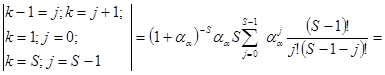
= 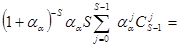

– Конец работы –
Эта тема принадлежит разделу:
По учебной дисциплине Телефония и военные коммутационные системы
ВОЕННАЯ АКАДЕМИЯ РЕСПУБЛИКИ БЕЛАРУСЬ... КАФЕДРА СВЯЗИ... УТВЕРЖДАЮ Начальник кафедры...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СМО С ПОТЕРЯМИ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов