рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Военное дело
- /
- ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ Двойной интеграл Двойной интеграл и его приложения
Реферат Курсовая Конспект
ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ Двойной интеграл Двойной интеграл и его приложения
ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ Двойной интеграл Двойной интеграл и его приложения - раздел Военное дело, Содержание Стр....
Содержание
стр.
Введение 4
1 Двойные и тройные интегралы 4
1.1 Двойной интеграл 4
1.1.1 Двойной интеграл и его приложения 4
1.1.2 Замена переменных в двойном интеграле 8
1.1.3 Примеры решения задач 10
1.2 Тройной интеграл 12
1.2.1 Тройной интеграл и его приложения 12
1.2.2 Замена переменных в тройном интеграле 15
1.2.3 Примеры решения задач 18
2 Криволинейные и поверхностные интегралы первого рода 19
2.1 Криволинейные интегралы первого рода 19
2.2 Примеры решения задач 21
2.3 Поверхностные интегралы первого рода 23
2.4 Примеры решения задач 24
3 Варианты заданий 26
Список литературы 43
Введение
Методические указания предназначены для студентов младших курсов всех специальностей бакалаврской подготовки в качестве руководства к выполнению типовой расчетной работы по теме «Кратные интегралы и теория поля».
Основная цель работы – привитие студентам практических навыков в решении задач по указанной теме. Проводится необходимый минимум теоретического материала, где рассмотрены методы вычисления кратных, криволинейных и поверхностных интегралов первого рода. Каждый раздел сопровождается решениями типовых задач. В конце методических указаний приводится 30 вариантов индивидуальных заданий по указанной теме.
ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
Двойной интеграл
Двойной интеграл и его приложения
Пусть ограниченная функция  определена в некоторой замкнутой области
определена в некоторой замкнутой области  плоскости
плоскости  Разобьем область
Разобьем область  произвольным образом на
произвольным образом на  меньших областей
меньших областей  не имеющих общих внутренних точек, в каждой части
не имеющих общих внутренних точек, в каждой части 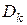 возьмем произвольную точку
возьмем произвольную точку  , вычислим значение
, вычислим значение 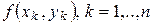 и составим сумму
и составим сумму

 (1.1)
(1.1)
где 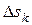 ― площадь
― площадь 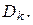
Эта сумма называется интегральной суммой функции 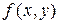 , соответствующей данному разбиению области
, соответствующей данному разбиению области  на части
на части  и данному выбору промежуточных точек
и данному выбору промежуточных точек 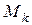 .
.
Диаметром ограниченного множества  назовем точную верхнюю грань расстояний между двумя произвольными точками этого множества:
назовем точную верхнюю грань расстояний между двумя произвольными точками этого множества: 
Пусть  ― диаметр
― диаметр 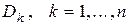 ,
,  .
.
Если существует предел интегральной суммы (1.1) при  не зависящий от способа дробления области
не зависящий от способа дробления области  на части
на части  и выбора точек
и выбора точек  в них, то он называется двойным интегралом от функции
в них, то он называется двойным интегралом от функции 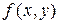 по области
по области  и обозначается
и обозначается
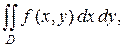
т. е. 
а функция 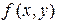 называется интегрируемой в области
называется интегрируемой в области  .
.
Если функция 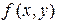 непрерывна в замкнутой области
непрерывна в замкнутой области  , то она интегрируема в этой области.
, то она интегрируема в этой области.
Двойные интегралы обладают такими же свойствами, как и определенные интегралы (линейность, аддитивность, формулы среднего значения и т. д.).
Геометрический смысл двойного интеграла: если 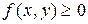 в области
в области 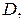 то двойной интеграл
то двойной интеграл
 (1.2)
(1.2)
численно равен объему цилиндрического тела 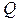 с основанием
с основанием  и образующей, параллельной оси
и образующей, параллельной оси  которое ограничено сверху поверхностью
которое ограничено сверху поверхностью  (рисунок 1.1).
(рисунок 1.1).
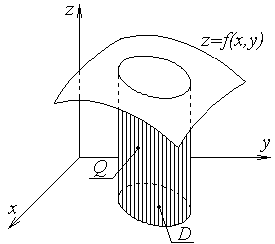
Рисунок 1.1
В частности, когда 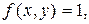 двойной интеграл (1.2) равен площади
двойной интеграл (1.2) равен площади  области
области 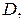 т. е.
т. е.
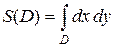 . (1.3)
. (1.3)
Физический смысл двойного интеграла: если область  ― плоская пластинка, лежащая в плоскости
― плоская пластинка, лежащая в плоскости  с поверхностной плотностью
с поверхностной плотностью 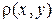 распределения вещества, то массу пластинки находят по формуле
распределения вещества, то массу пластинки находят по формуле
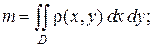 (1.4)
(1.4)
статические моменты пластинки относительно осей  и
и 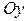 находят по формулам:
находят по формулам:
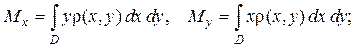 (1.5)
(1.5)
координаты центра масс пластинки:
 (1.6)
(1.6)
моменты инерции пластинки  относительно осей координат и начала координат:
относительно осей координат и начала координат:
 (1.7)
(1.7)
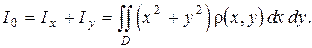
Область 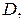 которая определяется неравенствами
которая определяется неравенствами 
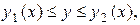 где
где 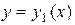 и
и  ― однозначные непрерывные функции на отрезке
― однозначные непрерывные функции на отрезке 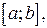 называется стандартной относительно оси
называется стандартной относительно оси 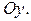 Аналогично определяется стандартная область относительно оси
Аналогично определяется стандартная область относительно оси 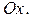
Область 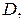 стандартную как относительно оси
стандартную как относительно оси  так и относительно оси
так и относительно оси 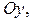 называют просто стандартной областью. На рисунке 1.2 показана стандартная относительно оси
называют просто стандартной областью. На рисунке 1.2 показана стандартная относительно оси  область
область 
В случае стандартной области  всякая прямая, параллельная оси координат и проходящая через внутреннюю точку
всякая прямая, параллельная оси координат и проходящая через внутреннюю точку 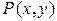 области
области 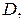 пересекает границу области в двух точках (рисунок 1.2).
пересекает границу области в двух точках (рисунок 1.2).

| 
|
Рисунок 1.2 Рисунок 1.3
Если  ― область интегрирования, стандартная относительно оси
― область интегрирования, стандартная относительно оси 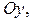 двойной интеграл вычисляется по формуле
двойной интеграл вычисляется по формуле
 (1.8)
(1.8)
Правую часть формулы (1.8) называют повторным интегралом, а интеграл
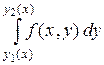
называют внутренним интегралом.
Вычисление повторного интеграла следует начинать с вычисления внутреннего, в котором переменную 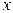 надо принять при интегрировании за постоянную величину. Результат интегрирования будет некоторой функцией от
надо принять при интегрировании за постоянную величину. Результат интегрирования будет некоторой функцией от  которая интегрируется затем по отрезку
которая интегрируется затем по отрезку  В результате получается некоторое число ― значение интеграла (1.8).
В результате получается некоторое число ― значение интеграла (1.8).
Если область  является стандартной относительно оси
является стандартной относительно оси  (рисунок 1.3), двойной интеграл вычисляется по формуле
(рисунок 1.3), двойной интеграл вычисляется по формуле
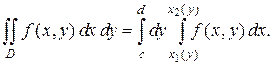 (1.9)
(1.9)
Процесс расстановки пределов интегрирования для внутреннего и внешнего интегралов называется приведением двойного интеграла к повторному, а переход от формулы (1.8) к формуле (1.9) или наоборот ― изменением порядка интегрирования.
Если область  не является стандартной ни относительно оси
не является стандартной ни относительно оси 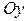 , ни относительно оси
, ни относительно оси  , ее разбивают на конечное число областей
, ее разбивают на конечное число областей 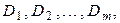 стандартных относительно оси
стандартных относительно оси 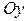 (или
(или  ), и при вычислении двойного интеграла по области
), и при вычислении двойного интеграла по области  используют свойство аддитивности.
используют свойство аддитивности.
Замена переменных в двойном интеграле
(1.10) Если между областями и , лежащими в плоскостях и (рисунок 1.4), установлено…Примеры решения задач
Задача 1.Вычислить двойной интеграл  по области
по области  , ограниченной кривыми
, ограниченной кривыми  и
и 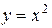 .
.
Решение. Область  является стандартной относительно оси
является стандартной относительно оси 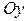 (рисунок 1.7)
(рисунок 1.7)
 Рисунок 1.7
Рисунок 1.7
| Сводим двойной интеграл к повторному по формуле (1.8):

|
Вычисляем внутренний интеграл в повторном, пользуясь формулой Ньютона-Лейбница:

Теперь вычисляем повторный интеграл:

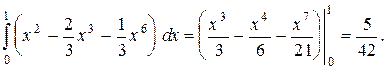
Задача 2. Найти объем тела 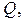 ограниченного поверхностями
ограниченного поверхностями 
Решение. Данное тело можно представить в виде  где
где  ― область на плоскости
― область на плоскости  ограниченная кривыми
ограниченная кривыми 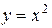 и
и  т.е.
т.е. 
Согласно геометрическому смыслу двойного интеграла объем тела 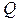

Задача 3. Найти моменты инерции относительно осей координат пластины с плотностью 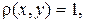 ограниченной кривыми
ограниченной кривыми 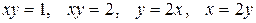 и расположенной в I квадранте.
и расположенной в I квадранте.
Решение. Данная пластина  изображена на рисунке 1.8.
изображена на рисунке 1.8.
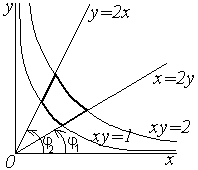 Рисунок 1.8
Рисунок 1.8
| По формулам (1.7) имеем 
 Для вычисления этих интегралов удобнее перейти к полярным координатам:
Для вычисления этих интегралов удобнее перейти к полярным координатам: 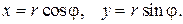
|
Тогда 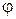 изменяется от
изменяется от 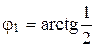 до
до 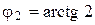 (рисунок 1.8), а при каждом значении
(рисунок 1.8), а при каждом значении 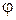 из отрезка
из отрезка 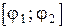 переменная
переменная  изменяется от
изменяется от  (значение
(значение  на кривой
на кривой 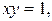 уравнение которой в полярных координатах в I квадранте имеет вид
уравнение которой в полярных координатах в I квадранте имеет вид  ) до
) до  ( значение
( значение  на кривой
на кривой  ). Следовательно, используя формулу (1.12), получим
). Следовательно, используя формулу (1.12), получим
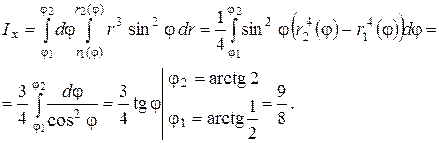
Аналогично получаем 
Тройной интеграл
Тройной интеграл и его приложения
Пусть в некоторой замкнутой ограниченной области 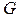 трехмерного пространства задана ограниченная функция
трехмерного пространства задана ограниченная функция 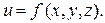 Произведем относительно области
Произведем относительно области 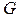 и функции
и функции 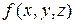 действия, подобные действиям при составлении суммы (1.1), в результате получим сумму
действия, подобные действиям при составлении суммы (1.1), в результате получим сумму
 (1.14)
(1.14)
где 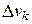 ― объемы частей
― объемы частей  на которые разбита область
на которые разбита область 
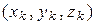 ― координаты точек
― координаты точек 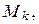 произвольно выбранных в этих частях области
произвольно выбранных в этих частях области 
Сумма (1.14) называется интегральной суммой функции 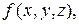 соответствующей данному разбиению области
соответствующей данному разбиению области 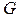 на части
на части  и данному выбору промежуточных точек
и данному выбору промежуточных точек 
Пусть  ― диаметр
― диаметр  ,
, 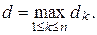
Если интегральная сумма (1.14) при  имеет предел, не зависящий от способа дробления области
имеет предел, не зависящий от способа дробления области 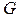 на части
на части  и выбора точек
и выбора точек 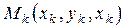 в них, то этот предел называется тройным интегралом от функции
в них, то этот предел называется тройным интегралом от функции 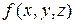 по области
по области 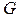 и обозначается
и обозначается
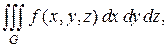 (1.15)
(1.15)
а функция  называется интегрируемой в области
называется интегрируемой в области 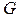 .
.
Всякая непрерывная в ограниченной замкнутой области 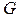 функция
функция  интегрируема в ней.
интегрируема в ней.
Тройные интегралы обладают такими же свойствами, как определенные и двойные интегралы ― линейность, аддитивность, формулы среднего значения и т.д.
Если в области 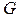 функция
функция  то тройной интеграл (1.15) равен объему области
то тройной интеграл (1.15) равен объему области 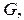 т. е.
т. е.
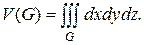 (1.16)
(1.16)
Если  считать объемной плотностью распределения вещества в области
считать объемной плотностью распределения вещества в области 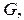 то интеграл (1.15) численно равен массе всего вещества, заключенного в области
то интеграл (1.15) численно равен массе всего вещества, заключенного в области 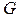 (физический смысл тройного интеграла).
(физический смысл тройного интеграла).
С помощью тройного интеграла можно также вычислить:
а) статические моменты тела относительно координатных плоскостей  и
и 

 (1.17)
(1.17)
где  ― плотность распределения вещества;
― плотность распределения вещества;
б) координаты центра масс тела:
 (1.18)
(1.18)
где  ― масса тела;
― масса тела;
в) моменты инерции тела относительно координатных плоскостей, координатных осей и начала координат:

 (1.19)
(1.19)

При вычислении тройных интегралов особую роль играет понятие стандартной трехмерной области, которое вводится по аналогии со стандартной двумерной областью. Так, например, область 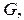 ограниченная снизу и сверху непрерывными поверхностями
ограниченная снизу и сверху непрерывными поверхностями 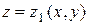 и
и 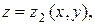 ― стандартная относительно оси
― стандартная относительно оси 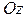 (рисунок 1.9).
(рисунок 1.9).

Рисунок 1.9
Она обладает следующими свойствами.
1. Всякая прямая, параллельная оси 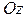 и проведенная через внутреннюю точку области
и проведенная через внутреннюю точку области 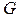 , пересекает границу области ровно в двух точках.
, пересекает границу области ровно в двух точках.
2. Вся область 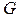 однозначно проецируется на плоскость
однозначно проецируется на плоскость  в двумерную область
в двумерную область  (рисунок 1.9).
(рисунок 1.9).
Тройной интеграл по области 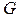 вычисляется так:
вычисляется так:

Здесь внутренний интеграл берется по  при фиксированных, но произвольных в
при фиксированных, но произвольных в  значениях
значениях 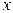 и
и  В результате получается некоторая функция
В результате получается некоторая функция  , которая интегрируется затем по области
, которая интегрируется затем по области  . Если область
. Если область ограничена линиями
ограничена линиями 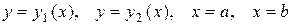 , то, переходя от двойного интеграла
, то, переходя от двойного интеграла  к повторному, получаем формулу
к повторному, получаем формулу
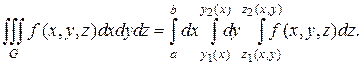 (1.20)
(1.20)
Если область 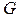 не является стандартной, то с помощью плоскостей, параллельных какой-либо из координатных плоскостей, разбивают ее на конечное число стандартных областей.
не является стандартной, то с помощью плоскостей, параллельных какой-либо из координатных плоскостей, разбивают ее на конечное число стандартных областей.
Замена переменных в тройном интеграле.
(1.21) которые однозначно разрешимы относительно : . (1.22)Примеры решения задач
Задача 1. Вычислить интеграл  если область
если область 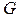 ограничена поверхностями
ограничена поверхностями  и
и 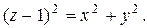
Решение. Уравнение конической поверхности, ограничивающей область 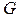 , можно записать в виде
, можно записать в виде 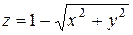 , а саму область
, а саму область 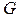 представить следующим образом
представить следующим образом  где
где  ― круг радиуса 1 с центром в начале координат (рисунок 1.12). Перейдем к цилиндрическим координатам
― круг радиуса 1 с центром в начале координат (рисунок 1.12). Перейдем к цилиндрическим координатам  где
где 
Подынтегральная функция в цилиндрических координатах равна
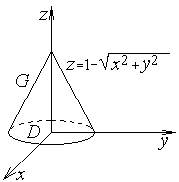 Рисунок 1.12
Рисунок 1.12
|  якобиан перехода к цилиндрическим координатам равен якобиан перехода к цилиндрическим координатам равен  Поэтому Поэтому 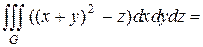


|

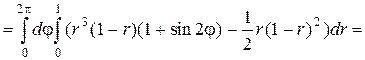

Задача 2. Вычислить массу тела, ограниченного поверхностью  и имеющего в каждой точке плотность
и имеющего в каждой точке плотность 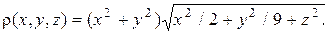
Решение. Поверхность, ограничивающая тело, является эллипсоидом, его каноническое уравнение  полуоси
полуоси 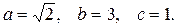
Согласно физическому смыслу тройного интеграла, масса тела, занимающего область 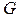 ,
,  Перейдем к обобщенным сферическим координатам
Перейдем к обобщенным сферическим координатам  следовательно, уравнение эллипсоида имеет вид
следовательно, уравнение эллипсоида имеет вид 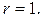 Поэтому для области
Поэтому для области 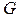 координата
координата  изменяется от 0 до 1, угол
изменяется от 0 до 1, угол  ― от 0 до
― от 0 до  , а угол
, а угол 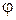 ― от 0 до
― от 0 до  Следовательно,
Следовательно,
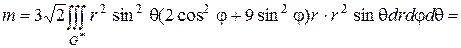
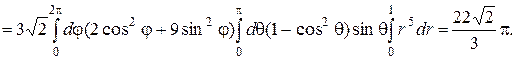
КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПЕРВОГО РОДА
Криволинейные интегралы первого рода
(2.1) где ― длина -й частичной дуги Пусть Если существует предел интегральной суммы (2.1) при не зависящей от способа дробления кривой на части и от…Примеры решения задач
Задача 1. Вычислить  где
где  ― часть эллипса
― часть эллипса  лежащая в I квадранте.
лежащая в I квадранте.
Решение. Параметрическое задание эллипса имеет вид 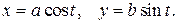 Поскольку рассматривается часть эллипса, лежащая в I квадранте, то
Поскольку рассматривается часть эллипса, лежащая в I квадранте, то  Поэтому, т.к.
Поэтому, т.к.  то применяя формулу (2.3), получим
то применяя формулу (2.3), получим


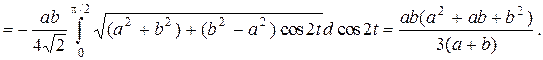
Задача 2. Вычислить  где
где  ― кривая, заданная уравнением
― кривая, заданная уравнением 
Решение. Перейдем к полярным координатам: 
 Уравнение кривой
Уравнение кривой  примет вид
примет вид  Для вычисления интеграла применим формулу (2.5). Так как
Для вычисления интеграла применим формулу (2.5). Так как 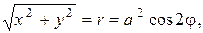
 то
то
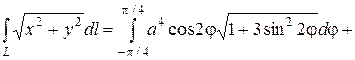


Задача 3. Найти массу  материальной кривой
материальной кривой  , заданной уравнением
, заданной уравнением 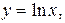 где
где  , если ее плотность
, если ее плотность 
Решение. По формуле для массы 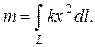 Для вычисления интеграла воспользуемся формулой (2.4). Так как
Для вычисления интеграла воспользуемся формулой (2.4). Так как  то
то 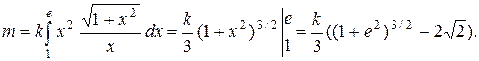
Поверхностные интегралы первого рода
(2.7) где ― площадь Пусть Если интегральная сумма (2.7) имеет предел при не зависящий от способа дробления поверхности на части и от…Примеры решения задач
Задача 1.Вычислить  где
где  - часть поверхности
- часть поверхности 
 вырезанная поверхностью
вырезанная поверхностью 
Решение. Поверхность  является частью параболоида
является частью параболоида  , отсеченной конусом
, отсеченной конусом  (рисунок 2.2).
(рисунок 2.2).
 Рисунок 2.2
Рисунок 2.2
| Поверхность  однозначно проецируется на плоскость однозначно проецируется на плоскость  в область в область  ― круг радиуса ― круг радиуса 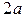 с центром в начале координат. Уравнение окружности с центром в начале координат. Уравнение окружности  , которая является границей , которая является границей  получается, если из уравнений получается, если из уравнений  и и  исключить исключить 
|
Разрешая уравнение  поверхности
поверхности  относительно
относительно  получаем
получаем 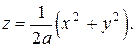 Следовательно,
Следовательно,  Поэтому, воспользовавшись формулой (2.11), получаем
Поэтому, воспользовавшись формулой (2.11), получаем
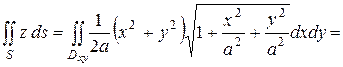
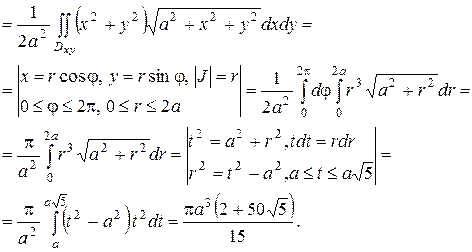
Задача 2.Найти массу поверхности сферы радиусом  если ее поверхностная плотность в каждой точке равна расстоянию от этой точки до вертикального диаметра.
если ее поверхностная плотность в каждой точке равна расстоянию от этой точки до вертикального диаметра.
Решение. Взяв за начало координат центр сферы и направив ось  по вертикали, получим, что расстояние от точки
по вертикали, получим, что расстояние от точки 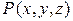 сферы до оси
сферы до оси  равно
равно 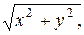 значит, плотность
значит, плотность  .
.
Согласно формуле (2.10)

где 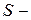 сфера, центр которой находится в начале координат.
сфера, центр которой находится в начале координат.
Для вычисления интеграла применим формулу (2.13), поэтому запишем параметрическое представление сферы 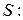
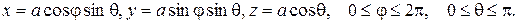
По формулам (2.14) вычислим

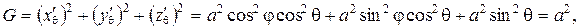
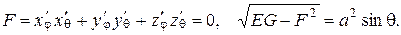
Следовательно, 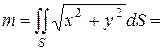


ВАРИАНТЫ ЗАДАНИЙ
Первые пять задач каждого варианта необходимо решить при следующих условиях:
1. Изменить порядок интегрирования в двойном интеграле.
2. Найти координаты центра тяжести однородной фигуры, ограниченной данными линиями.
3. Найти площадь части поверхности 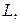 вырезаемой поверхностью
вырезаемой поверхностью  .
.
4. Найти объем тела, ограниченного заданными поверхностями.
5. Найти массу тела плотности  ограниченного данными поверхностями.
ограниченного данными поверхностями.
Вариант № 1
1. 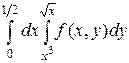 .
.
2. 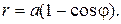
3. 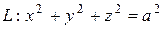 ,
, 
4. 
5. 
6. Найти длину кардиоиды 

7. Вычислить площадь части поверхности параболоида  ограниченной плоскостью
ограниченной плоскостью 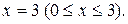
Вариант № 2
1. 
2. 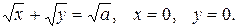
3. 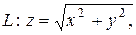
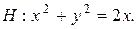
4. 
5. 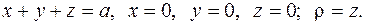
6. Вычислить координаты центра тяжести однородной дуги астроиды  расположенной в I квадранте.
расположенной в I квадранте.
7. Найти массу сферы  если поверхностная плотность в каждой точке равна расстоянию от этой точки до оси
если поверхностная плотность в каждой точке равна расстоянию от этой точки до оси  .
.
– Конец работы –
Используемые теги: Двойные, Тройные, Интегралы, двойной, интеграл, двойной, интеграл, ложения0.11
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ Двойной интеграл Двойной интеграл и его приложения
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов